1. Problem modeling

   1. Data
      • L: Number of layers
      • HS: list of hits
      • N: The number of hits 
      • NL: the number of hits excludes the last layer
      • h_i , i = [1, N], hit number i in HS
      • (x_i, y_i): coordinate of hit h_i .
      • β_{i, j, k} : is a linear pair angle created by two segments (h_i, h_j) and (h_j, h_k).
      • d_{i, j} : is the distance between h_i and h_j
   2. Variable
      •  x_{i, j} : a decision binary variable of segment (h_i, h_j) :
        • x_{i, j} = 1, assign segment (h_i, h_j) at a track
        • x_{i, j} = 0, otherwise.

2. Workflows

   We will introduce a baseline model (Quadratic Constrained Binary Model - QCBM) and expand to two models (Quadratic Unconstrained Binary Model - QUBM and Binary Linear Program - BLP).

   We leverage Cplex and Dwave to solve problems appropriately.

   

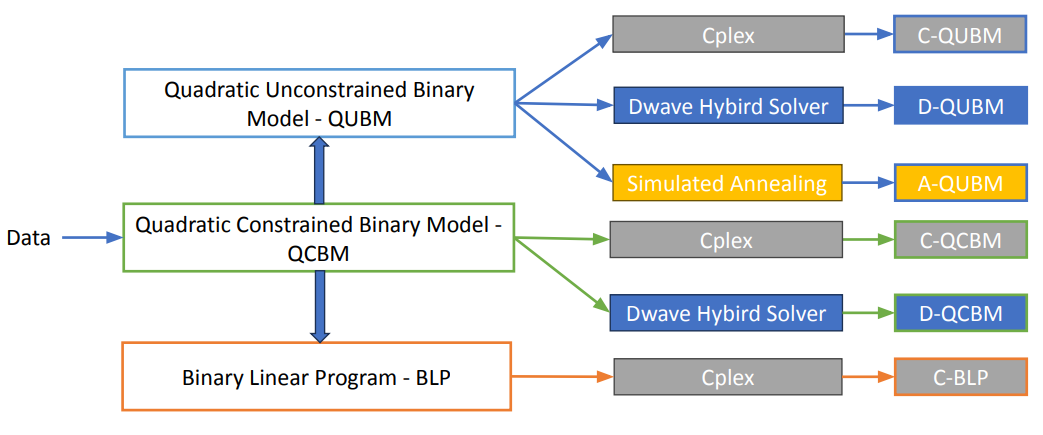
3. Quadratic Constrained Binary Model - QCBM

   QCBM has two separate parts:

   1. Objective cost function
   2. Constraints
   

   We can leverage Cplex to solve quadratic problem (C-QCBM) and hybrid solver of D-wave to solve quadratic binary model (D-QCBM).

4. Quadratic Unconstrained Binary Model - QUBM

   To convert QCBM to QUBM, we use penalty terms to replace constraints, as shown in the figure below:

   

   
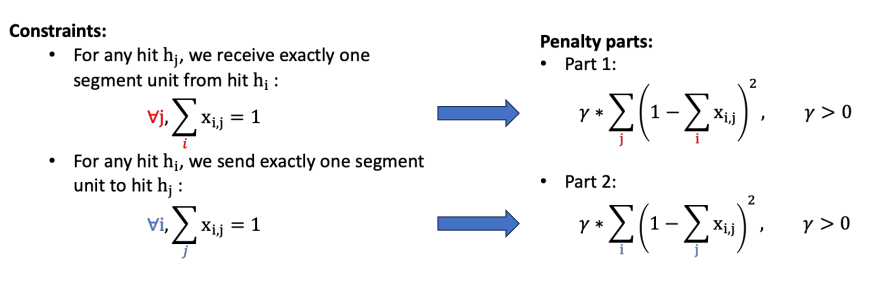
   We add penalty parts to the objective function of QCBM to get QUBM. QUBM can be represented as a Hamiltonian: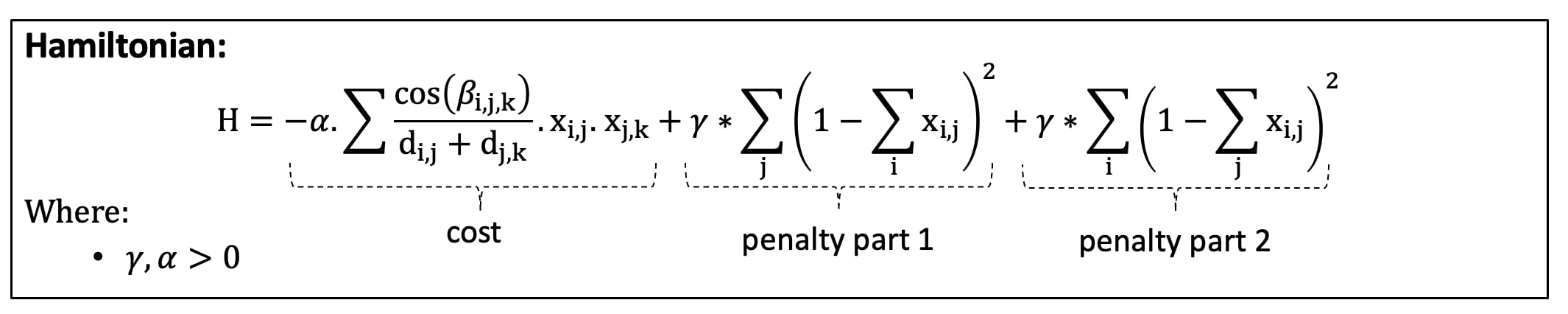

   

   With this Hamiltonian, we can use Cplex to solve (C-QUBM), a D-wave hybrid solver (D-QUBM), and simulated annealing (A-QUBM).

5. Binary Linear Program - BLP

   The figure below represents converting the quadratic binary model to a linear binary model with additional constraints.

   

   We replace the quadratic part in the cost function and add additional constraints to the constraints part of QCBM to get BLP, as shown in the figure below:

   

   We can use Cplex to solve the binary linear model (C-BLP) with this model.

Remarks on CPLEX

The tools is provided by IBM
and can be downloaded here

Remarks on Python code that used Dwave library : Method_D_QCBM

1) Python code must have the following line :
from dwave.system import LeapHybridCQMSampler
2) The Hybrid Dwave solver is used using a variable and should be similar to :
sampler = LeapHybridCQMSampler()
This line should create the following error : "API token not defined"
3) How to fix the problem ?
3.1) Create an account on dwave
on the Dwave page
3.2) Copy the API token at your web page


3.3) Install D-wave Ocean tool

The documentation is here .
D-wave Ocean tool is required Python >= 3.8

Do first: pip install dwave-ocean-sdk

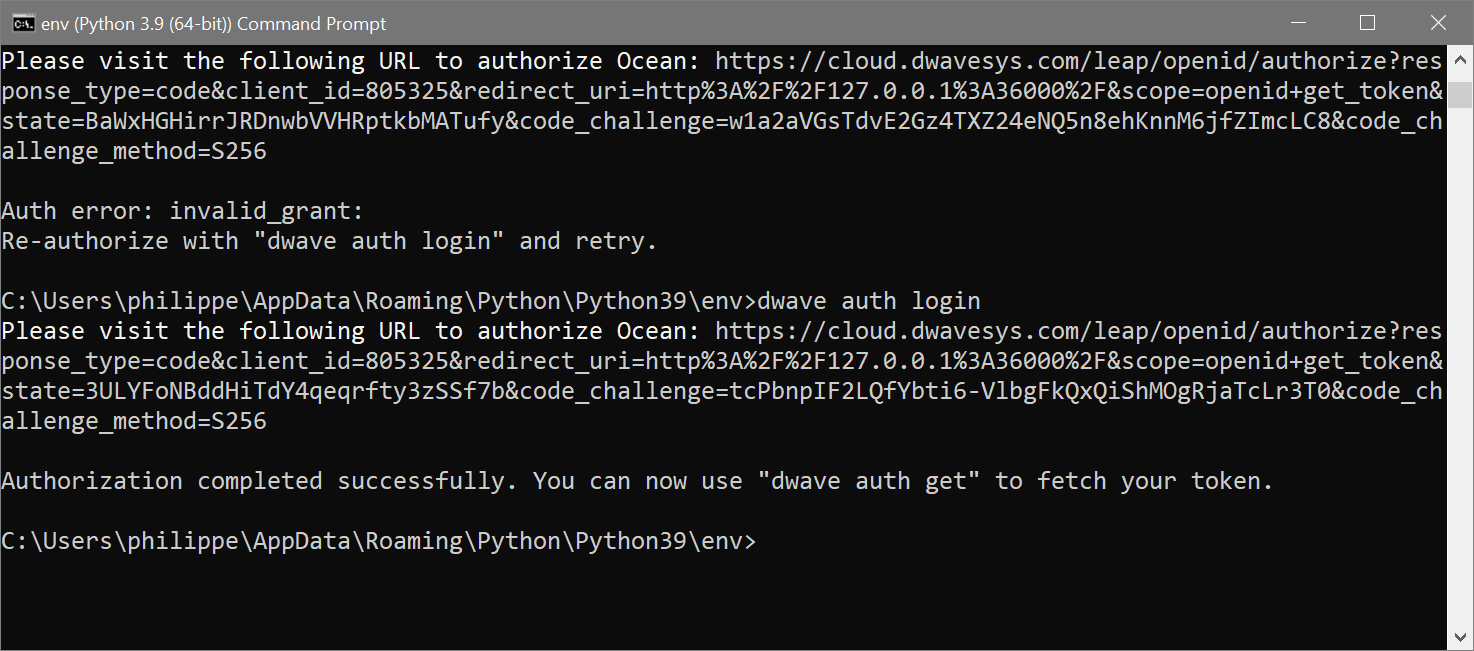
Do Second: on the console, use the following command line dwave auth login
A web page should appear in your web browser and you have to accept the connection
If it succeed you should have the following prompt.



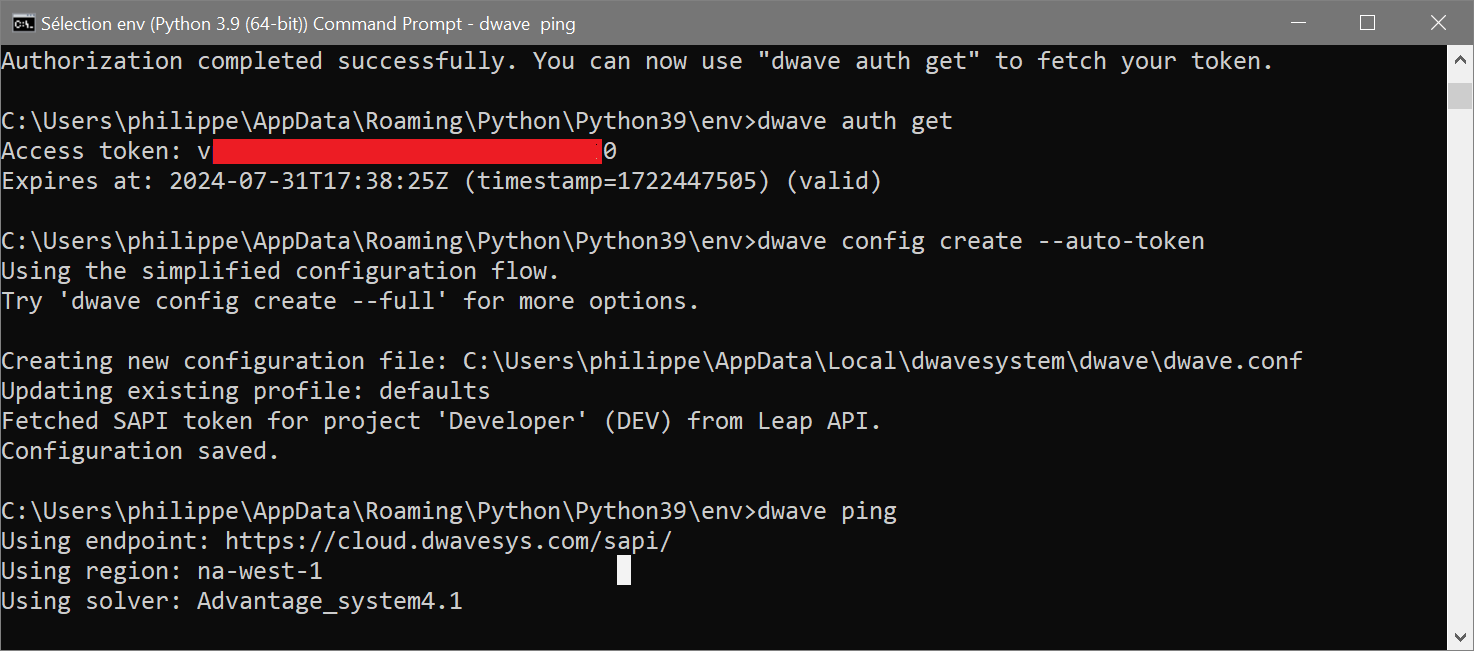
Do Third: on the console, use the following command line dwave config create --auto-token
Do next: on the console, use the following command line dwave ping
You should have some like that if everything is nice.

In conclusion, we defined three models (QCBM, QUBM, BLP) to solve the track-finding problem with the technical from Cplex and Dwave.