Numerical Codes

Jonas KOKO : Associate Professor in Applied Mathematics

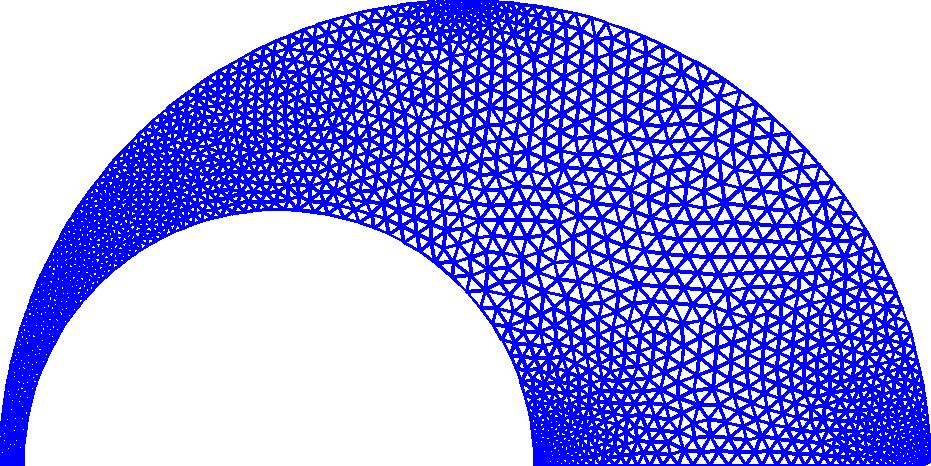
KMG2D : 2D Mesh Generator using signed distance function and a geometric mesh size function

kmg2d is a 2D MATLAB/OCTAVE mesh generator based on signed distance function, i.e. the domain Ω must be defined as

Ω={x | φ(x)<0}

where φ is a real-valued function defined on R². The code generates unstructured (linear or quadratic) triangular mesh. The mesh size is automatically adapted to the "thickness" of the computational domain, using a geometric mesh size function based on distance from the medial axis. The medial axis is the set of interior points that have equal distance to two or more points on the boundary. Computing the medial axis of a domain requires solving of the eikonal equation

||∇ φ(x)|| = 1.

To save computational time, the code uses an approximate medial axis set. The code can also use a user supplied mesh size function.

The names of the functions and their purposes:

kmg2d.m the mesh generator, designed to generate medium-scale meshes
kmg2dref.m the fast mesh refinement function
hgeom.m the geometric mesh size function

Package: kmg2d

Reference : J. Koko, A MATLAB mesh generator for the two-dimensional finite element method, Applied Mathematics and Computation 250, 650-664 (2015).

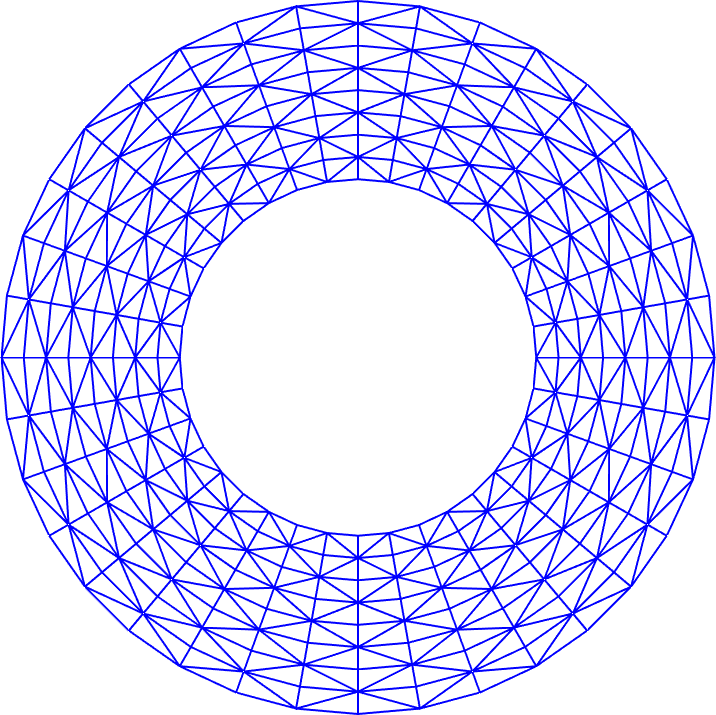
Uniform mesh generation for domains with simple geometry (New)

Two-dimensional domain: kmg2du.m

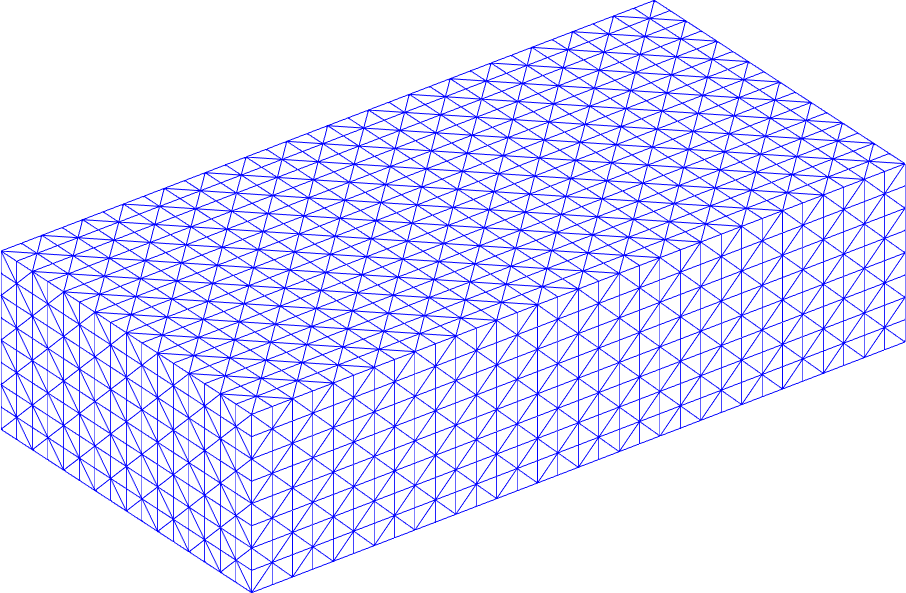
Three-dimensional domain: kmg3du.m

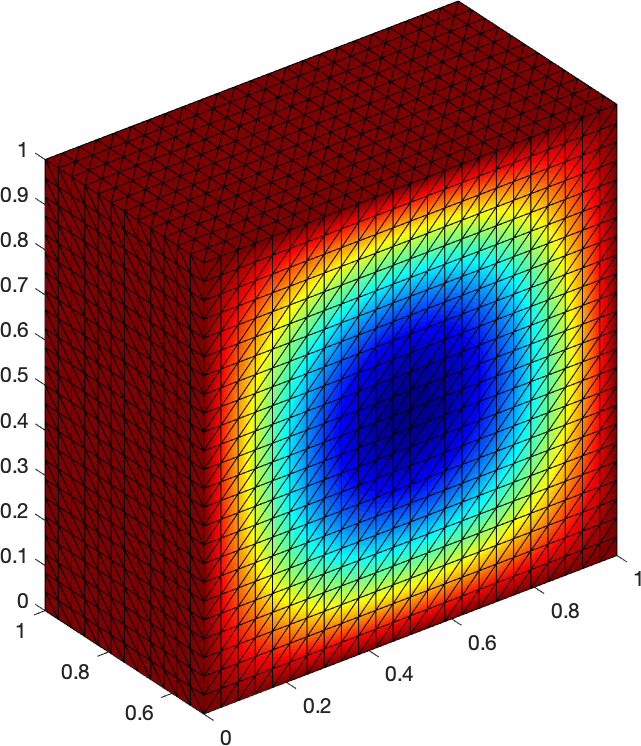
KPDE : Fast FEM assembling functions for the Poisson problem and the linear elasticity in 2D/3D

kpde is a vectorized MATLAB/OCTAVE library of P¹ finite element assembling functions for the numerical solution of the Poisson problem and the linear elasticity problem in 2D/3D. Cell-arrays are used to store the gradient of the element basis functions. The resulting vectorized MATLAB implementation, close to the standard form, is fast and scalable. The code consists of 3 sets of functions

kpde2d/kpde3d vectorized functions for the general 2D/3D scalar Partial Differential Equation

−∇.(ν(x)∇ u(x))+α(x)u(x)=f(x) in Ω

kelas2d/kelas3d vectorized function for 2D/3D linear elasticity problem

−∇.σ(u(x))=f(x) in Ω.

Pre and post-preocessing functions: uniform mesh generation (kpde2dumsh, kpde3dumsh), visualization (kpde2dcont, kpde3dshow, kelas2dshow, kelas3dshow), ...

Package: kpde

Reference: J. Koko, Fast MATLAB assembly of FEM matrices in 2D and 3D using cell-array approach, International Journal of Modeling, Simulation and Scientific Computing 7 (2), 1650010, 2016, DOI: 10.1142/S1793962316500100.

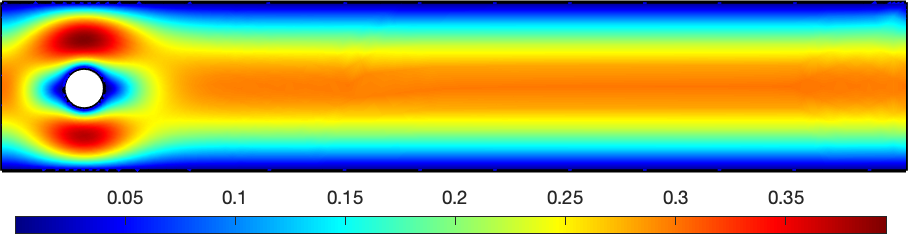
KSTOK : Fast assembling functions for the Stokes equation with mini-element (P1-bubble/P1) in 2D/3D.

kstok is a vectorized MATLAB assembling functions for the numerical approximation of the Stokes problem using P1-bubble/P1 finite element in 2D and 3D. The implementation uses cell-array to store the gradient of the element basis functions. Consequently, the current code is about two times faster than the previous one (see below). Note that, the code shares some functions with kpde package. The code consists of 3 sets of functions

kstok2dp1/kstok3dp1 Vectorized assembling functions for the mini-element ( P1-bubble/P1 ) in 2D and 3D.

kstokcg Preconditioned Uzawa conjugate gradient solver for the saddle-point equation

Pre and post-preocessing functions: uniform mesh generation (kpde2dumsh, kpde3dumsh) and visualization

Package: kstok

Reference: J. Koko, Efficient MATLAB codes for the 2D/3D Stokes equation with the mini-element , Informatica 30 (2), 243-268, 2019.