Projet apprentissage par renforcement
Table des matièresClose
1 Présentation
 Le projet se décompose en deux phases, correspondant chacune approximativement à une semaine de
travail. La première phase est commune à tous les groupes et met en place des outils permettant de manipuler des images
et d'interagir avec l'utilisateur. Cette phase est ponctuée de petits exercices assez libres où vous devrez démontrer
votre maîtrise des points abordés en individuel et se termine par la création d'un petit jeu d'arcade en groupe qui
mettra de plus en œuvre un processus Markovien. La seconde phase, plus spécifique à chaque groupe, consiste à
réinvestir les acquis de la première phase afin de créer un prototype de votre propre « jeu vidéo » respectant la
thématique du projet.
Le projet se décompose en deux phases, correspondant chacune approximativement à une semaine de
travail. La première phase est commune à tous les groupes et met en place des outils permettant de manipuler des images
et d'interagir avec l'utilisateur. Cette phase est ponctuée de petits exercices assez libres où vous devrez démontrer
votre maîtrise des points abordés en individuel et se termine par la création d'un petit jeu d'arcade en groupe qui
mettra de plus en œuvre un processus Markovien. La seconde phase, plus spécifique à chaque groupe, consiste à
réinvestir les acquis de la première phase afin de créer un prototype de votre propre « jeu vidéo » respectant la
thématique du projet.
1.1 Synopsis pédagogiques
1.1.1 Gestion de projet
Votre groupe doit mener le travail à bout, vous devez donc créer une synergie de groupe qui vous permettra d'obtenir des livrables de qualité maximale, dans une ambiance de travail agréable et productive. Le projet se déroule sur un temps plus long que le temps d'un TP, vous avez donc un peu de temps pour vous tromper mais pour parvenir à un rendu de qualité, une bonne gestion de votre temps s'impose.
Vous devez également apprendre à utiliser Git… et l'utiliser de façon efficace.

Figure 1 : Logo git
Vous devrez de plus maintenir au fil de votre projet une page web sur le site de l'ISIMA. Cette page devra proposer un lien sur votre dépôt git, des informations sur l'état du projet, et servira de support lors des deux présentations. Il est important que votre page soit tenue à jour, au minimum de façon journalière.
Attention
- vous devez pouvoir présenter des
fiches/diagrammes de répartition des tâches (prévisionnelles,
effectives) à jour à tout moment,
- chacun doit créer plusieurs commits par jour et au moins un push chaque jour,
- les branches (git) doivent être utilisées : à
chaque nouvelle fonctionnalité correspond au moins une branche.
1.1.2 Programmation
Chacun d'entre-vous doit à la fin de ce projet avoir atteint un niveau minimal dans la qualité de son code, et en particulier, vous devrez :
- Maîtriser la syntaxe du c,
- Savoir utiliser à bon escient des bibliothèques standards,
- Savoir rechercher rapidement de l'information dans le man / sur le net,
- Comprendre l'utilisation des makefiles,
- Savoir documenter votre code : code le plus possible auto-documenté (les noms de variable, la présentation du code sont si lumineux que d'autres explications sont superflues) qu'on pourra compléter si nécessaire par des fichiers d'explications en org mode ou markdown et potentiellement doxygen,
- Savoir réaliser une page web présentant votre travail.
1.1.3 Algorithmique
Au cours du TP vous allez réinvestir vos acquis en algorithmique ainsi qu'en structures de données. Le projet utilisera au minimum des listes, tableaux, arbres, graphes et vous demandera de les manipuler et parcourir de façon adaptée.
Le terme 'liste' est souvent utilisé dans ce document pour simplement signifier 'énumération' et n'implique pas de façon de l'implémenter.
1.1.4 Outils pour les interfaces
Le projet doit vous permettre de découvrir ou d'approfondir vos connaissances dans le domaine de la programmation graphique 2D. Vous devrez notamment :
- (Re?-)Découvrir la SDL2,
- Créer une image par juxtaposition et superposition d'autres images,
- Gérer la transparence dans la superposition de deux images,
- Créer une animation simple,
- Gérer une boucle d'évènements,
- Gérer les entrées utilisateur.
1.2 Évaluation
 Le projet est évalué avec les mentions suivantes : TB+F (Très Bien avec Félicitations du jury), TB (Très Bien), B
(Bien), AB (Assez Bien), DFSP (Doit Faire Ses Preuves), I (Insuffisant).
Le projet est évalué avec les mentions suivantes : TB+F (Très Bien avec Félicitations du jury), TB (Très Bien), B
(Bien), AB (Assez Bien), DFSP (Doit Faire Ses Preuves), I (Insuffisant).
Le projet est validé si la mention obtenue est au moins Assez Bien.
L'évaluation prendra notamment en compte les points suivants :
- Sérieux, persévérance, implication, quantité de travail, régularité,
- Git : 'commits' et 'push' réguliers,
- Web : régularité de la maintenance et pertinence des informations,
- Collaboration dans le groupe,
- Qualité du travail (codes, documentations, rendus, utilisation des outils),
Le résultat de l'évaluation ne sera pas nécessairement identique pour tous les membres d'un groupe.
Certains projets ou éléments de projets seront conservés afin d'être utilisés à fin de démonstration ou comme base de futurs travaux : n'utilisez que des images, sons, planches de sprites (assets), etc… libres de droits.
1.3 Présentations du travail
L'évaluation se fera sur la durée des deux semaines, avec en particulier deux temps fort où vous réaliserez une soutenance de votre travail, chacun des deux vendredis.
La durée prévue des soutenances est d'environ 10 minutes (6 minutes de présentation, 4 pour les questions).
Dans l'éventualité où la première soutenance n'aurait pas été concluante, une troisième présentation pourra être imposée le lundi de la deuxième semaine.
1.4 Groupes
Le travail est à réaliser en groupes libres de trois étudiants, les groupes ne doivent pas nécessairement respecter les groupes classes habituels (un groupe peut mixer un G31 avec deux G11…).
Si des étudiants ne parviennent pas à compléter leur groupe avant la date du début du projet, les groupes seront alors imposés par l'équipe enseignante (en général cela ne présage pas d'un excellent projet lorsque vous arrivez le lundi matin sans avoir trouvé vos coéquipiers…).
1.5 Présence obligatoire
La présence est obligatoire de 9h à 12h et de 13h30 à 16h30 du lundi au jeudi pendant les deux semaines de projet, et les vendredis de 9h à 12h et de 13h30 à 17h00.
Les deux vendredis, il est possible que votre groupe ait une soutenance en dehors des plages horaires indiquées ci-dessus ou que des retards imposent un dépassement des horaires prévus.
Il est recommandé d'avancer le projet en dehors des créneaux indiqués ;).
1.6 Phases du projet
1.6.1 Deux phases
Durant la première semaine du projet, les apprentissages sont guidés. Ils ont pour vocation à vous familiariser avec la création de graphiques, d'animations en 2D. Les premiers exercices sont individuels, afin que chacun dispose d'un socle commun, puis dans la deuxième moitié de la semaine, un premier travail de groupe est réalisé, un petit jeu d'arcade vous permettant de mettre en œuvre vos acquis.
La seconde phase vous permettra à votre groupe de créer une application plus conséquente de votre choix, respectant les contraintes ainsi que la thématique imposées.
1.6.2 Personnalisation des exercices
Les exercices demandés acceptent des variations, acceptables tant qu'elles vous permettent de démontrer votre savoir-faire sur le point étudié. Le but n'est pas de plagier les exemples proposés, mais de démontrer votre savoir-faire ! Pensez cependant à faire valider vos propositions de variations par un enseignant afin :
- de ne pas vous lancer dans un travail trop chronophage par rapport à la version originale,
- de ne pas avoir manqué un point particulier que les enseignants désirent vous voir démontrer.
1.7 Récapitulatif des travaux à réaliser
La liste des programmes à réaliser, dont un contenu plus précis sera détaillé dans la suite du document est :
- X fenêtré : travail individuel
- Savoir ouvrir, fermer, déplacer, redimensionner des fenêtres graphiques.
- Pavé de serpents : travail individuel
- Savoir dessiner des formes géométriques, les animer.
- Jeu de la vie : en groupe, mais tout le monde fait la même chose (pas de répartition du travail)
- Animer des formes géométriques, gestion de la souris.
- Animer des sprites : individuel
- Créer une animation possédant un fond (si possible en mouvement), et un sprite qui se déplace sur ce fond.
- Chef d’œuvre : travail de groupe
- Créer un jeu d'arcade simple démontrant votre maîtrise de toute la partie graphique étudiée précédemment, ainsi que la partie sur les chaînes de Markov. Ce travail termine la première semaine.
- Jeu avec apprentissage pzar renforcement : travail de groupe
- Créer un jeu graphique, avec utilisation de l'apprentissage par renforcement.
1.8 Machines
1.8.1 Machines virtuelles
Afin de pouvoir travailler de la façon la plus agréable possible, il est possible d'utiliser une machine virtuelle personnelle fournie par l'ISIMA sur laquelle vous êtes administrateurs. Être administrateur vous permettra d'installer les logiciels de votre choix, et de configurer à votre guise le système d’exploitation.

Pour rappel, il est nécessaire de démarrer la machine virtuelle avant de pouvoir l'utiliser sur guacamole, ou en s'y
connectant via ssh ssh -Y login@nom_machine, où à l'aide de remmina. Il peut être nécessaire de reconfigurer le
password (vous pouvez mettre celui de l'ENT ici).
- Pour remmina
- choisir rdp (remote desktop protocol)
- nouveau profil de connexion
- Name : votre choix
- Group : isima
- Protocol : doit déjà être rempli avec RDP
- Server : vm-etu-login où login est à remplacer par votre login
- Password : vous le mettez ou non…
- Domain : local.isima.fr
- … si besoin, remplissez les option de votre choix …
- Resolution : use client resolution
- Save !!!
- sur l'écran principal, dans les préférences (
CTRL p), dans l'onglet RDP (tout en bas), cocher 'use client keyboard mapping' pour conserver votre configuration du clavier. Parfois, cela ne suffit pas (???), il faut alors rechercher dans la liste qui précède cette case à cocher un clavier approprié.
- Précautions
Cette machine virtuelle n'est pas 'garantie', elle peut être effacée, remplacée, modifiée à tout moment. Il est par conséquent important que vos document soient présents dans un endroit fiable, par exemple le répertoire 'shared'.
Une astuce pour disposer aisément de vos fichiers de config si vous utilisez plusieurs machines, est de les placer dans le répertoire 'shared', et de placer un un lien symbolique vers ces fichiers. Par exemple, pour récupérer une configuration emacs placée dans 'shared' :
ln -s "~/shared/.emacs.d" "~/.emacs.d"
Évidemment, les risques de perdre beaucoup de votre travail sont quasi nuls, même si votre ordinateur personnel est capturé par des aliens, car il vous est obligatoire de faire des commits et des pushs très régulièrement.
Dans l'éventualité ou le répertoire 'shared' ne serait pas monté, la commande
kinitpermet parfois de résoudre le problème (essayer au moins trois fois).
1.8.2 Machines personnelles
Vous pouvez utiliser votre ordinateur personnel, que ce soit avec une distribution Linux ou WSL pour Windows… mais dans tous les cas il vous est demandé de faire de la programmation sous Linux, et non sous Windows.
2 Chaine de Markov
2.1 Présentation

Le but de cette partie est de présenter comment à l'aide de chaines de Markov, il est possible de simuler des comportements intéressants, comme par exemple le choix des actions d'un personnage dans un jeu afin de simuler un comportement 'intelligent'.
On note les états possibles d'un système. On définit la variable aléatoire qui associe à une date de temps l'état à cette date du système. On suppose connue la loi de probabilité (sachant dans quel état se trouve le système à une date de temps, on connaît la probabilité que le système se trouve dans chacun des états à la date suivante).
Pour simplifier, on peut penser que cette loi est indépendante de , mais pour cet exposé (qui ne va en réalité n'utiliser à peu près aucun des résultats mathématiques sur le sujet), cela n'a en réalité que peu d'importance, et on pourra coder des lois qui dépendent du temps (par exemple, le comportement d'un agent se modifie selon le cycle jour/nuit, les saisons, son âge, …, et donc les probabilités de transiter de transiter d'une action à une autre sont dépendantes du temps).
En termes de représentations, on aime souvent représenter la loi de probabilité par une matrice telle que est la probabilité à la date de transiter de l'état vers l'état , c'est à dire : (même si au final ce n'est pas important si on reste parfaitement cohérent, il est dans la pratique important de ne pas se mélanger les pinceaux entre les 'départs' qui correspondent aux indices de lignes et les 'arrivées' qui correspondent aux indices des colonnes).
La représentation matricielle n'est pertinente que si la matrice ne possède pas trop de zéros, et qu'il n'y a pas trop de répétitions de valeurs. Si ce n'est pas le cas, on peut utiliser un tableau de listes chainées, où l'indice dans le tableau correspond à la situation de départ, et les éléments dans chaque liste chainée indiquent des actions et leurs probabilités de réalisation ; dans certains cas on utilise une fonction qui contient des tests sur les valeurs de et pour choisir la valeur.
2.2 Exemple
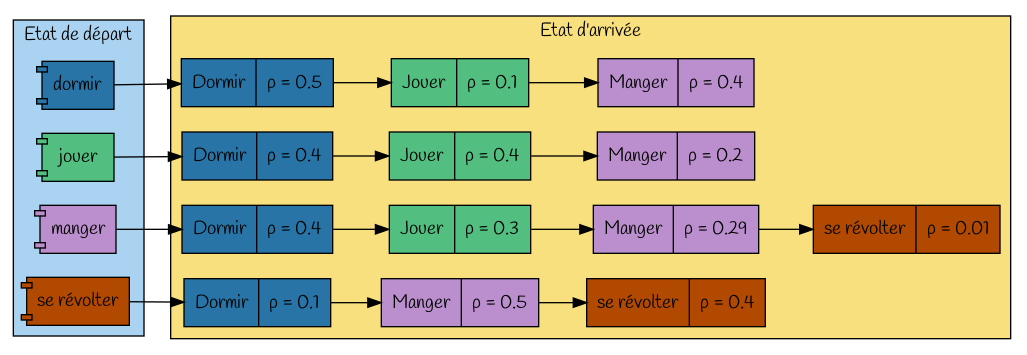
La table (matrice lorsqu'on se limite aux valeurs numériques à son centre) des transitions est une façon de représenter aisément les probabilités de transition.
|
Table des probabilités de transition |
Alors à la date t+1 la nouvelle action sera |
||||
| dormir | jouer | manger | se révolter | ||
|
Si à la date t l'action est |
dormir jouer manger se révolter |
0.5 0.4 0.4 0.1 |
0.1 0.4 0.3 0 |
0.4 0.2 0.29 0.5 |
0 0 .01 0.4 |
La première ligne s'interprète par : si le système est dans l'état 'dormir' à une date de temps, à la date suivante
- il y a 50% de chances qu'il continue à dormir,
- il y a 10% de chances qu'il aille jouer,
- il y a 40% de chances qu'il aille manger
- il n'y a aucune chance qu'il se révolte.
Remarque : la somme d'une ligne vaut toujours 1, car partant d'un état, il faut bien être quelque part à l'état suivant, par contre il n'y a aucune particularité notable sur la somme d'une colonne.
Important
Connaissant l'état du système à une date donnée, pour
générer un état à la date suivante respectant la distribution de
probabilité,
on extrait la ligne qui correspond à l'état en cours, et on
tire le nouvel état en suivant la loi tabulée définie par cette ligne.
2.3 Quelques propriétés simples et utiles
si on note le vecteur (ligne) qui indique la probabilité de se trouver dans chacun des états à la date :
on a alors une relation qui lie les distributions de probabilité aux dates et :
- puissance itérée de la matrice : en itérant fois le résultat précédent dans le cas où est indépendante de , on obtient alors la probabilité de passer de l'état à l'état en étapes : .
- il est également possible d'obtenir des informations sur la distribution des états à long terme, l'espérance de la longueur d'un cycle, etc… Ces résultats sont très utiles, mais nécessitent une certaine quantité de définitions qui permettent en particulier de bien cerner leur domaine de validité.
2.4 Avantages et inconvénients
- Les points positifs de cette façon de simuler des comportements sont
- une fois les états définis, inventer les valeurs sur une ligne n'est pas extrêmement difficile, nous n'avons besoin que de nous focaliser sur ce qui se passe juste après un certain état. Cette simplicité provient principalement de la propriété d'absence de mémoire dans cette modélisation (une fois que le système à atteint un état, il n'est pas possible de retrouver de quel état il provenait),
- faire des systèmes possédant des comportements différents (personnalités) est assez simple, on peut par exemple augmenter la probabilité d'un comportement que l'on veut favoriser,
- même si plusieurs systèmes possèdent exactement les mêmes paramètres, ils n'auront pas le même comportement,
- Simuler ce qui se passe pour le système est simple.
- Les points négatifs de cette façon de simuler sont
- si le nombre d'états est important, la table devient vite gigantesque (le carré du nombre d'états). Cela n'engendre normalement pas de problème de mémoire (il faudrait tout de même un grand nombre d'états avant d'atteindre des tables de grande taille), mais il est alors nécessaires de trouver des valeurs à entrer dans la table (c'est là qu'en réalité le bât blesse). Pour limiter cet effet (mais au prix d'une augmentation de la complexité du modèle et du code), on peut définir des macro-états, qui eux se décomposent en sous états. En reprenant l'exemple précédent, on pourrait affiner la partie 'se rebeller' en une table comprenant comme états 'contre les bleus', 'contre les verts', 'contre les arc-en-ciel'. Cela a pour avantage de diminuer la taille du modèle mais perd de l'expressivité. On pourra par la première table passer de 'manger' à 'se rebeller', puis avec la seconde table déterminer contre qui se fait la rébellion, mais il ne sera pas possible de passer directement de 'manger' à 'se rebeller contre les verts'.
- si on désire obtenir des comportements particuliers sur le long terme, il peut être difficile de fixer les valeurs des probabilités de transition.
2.5 Raffinements
2.5.1 États ou actions impossibles
Parfois, toutes les actions ne sont pas possibles. Par exemple, si on désire simuler un système qui peut se déplacer dans les directions Nord, Sud, Est, Ouest avec certaines probabilités (ses préférences pour chacune des directions), il pourrait être nécessaire de prévoir les différentes situations : on ne peut pas aller à l'est, on ne peut aller ni au nord, ni à l'est, … ce qui va ajouter beaucoup d'états !
Une solution simple à ce problème est : on construit la table sans se préoccuper de ce qui est possible, et au moment de choisir l'action, on normalise le vecteur ligne.
- Maths
On s'intéresse à la situation où l'état est impossible, et on calcule la probabilité de transiter de l’état vers l'état (avec évidemment )
- Algo qui en découle
Entrée :
- P la matrice des transitions
- i et k
Sortie :
- un entier j qui est une réalisation de la v.a. S, partant de l'état s_j et interdisant d'arriver sur l'état s_k
Processus :
- Définir normalisation = 0
- Pour l = 0 à n-1
- si l != k // s'il y a d'autres états interdits, il suffit de ne pas les ajouter à 'normalisation'
- normalisation += P[i][l]
- Définir alpha : un réel tiré en aléatoire uniforme dans [0 ; 1[
- définir n le nombre d'états possibles
- Définir j = n-1 // par défaut, le programme renvoie la dernière réalisation possible
- Définir cumul = 0 // on construit les probabilités cumulées
- Pour l = 0 à à n-2 :
- cumul += P[i][l]/normalisation
- Si alpha < cumul :
- i = l
- break
- renvoyer i
Il est possible de pousser encore un peu plus loin cette idée : si on sait par avance que deux actions sont incompatibles, alors on peut avoir la somme des éléments d'une ligne strictement supérieure à 1, à condition que la somme vaille 1 pour toute combinaison ne comportant pas d'impossibilité. Cela permet alors de modéliser assez simplement des comportements du type : si la porte est ouverte, alors j'avance, sinon je fais autre chose.
2.5.2 Action perdurant pendant plusieurs cycles
Si une action dure plusieurs dates de temps, il est alors nécessaire de la décomposer en plusieurs états. Ainsi, si on peut dormir pendant 3 ou 4 dates de temps, on définit les états :
- dormir 1
- dormir 2
- dormir 3
- dormir 4
Et on peut par exemple modifier la table du début en :
| dormir 1 | dormir 2 | dormir 3 | dormir 4 | jouer | manger | se révolter | |
|---|---|---|---|---|---|---|---|
| dormir 1 | 1 | ||||||
| dormir 2 | 1 | ||||||
| dormir 3 | 0.2 | 0.3 | 0.3 | 0.15 | 0.05 | ||
| dormir 4 | 0.1 | 0.4 | 0.45 | 0.05 | |||
| jouer | 0.4 | 0.4 | 0.2 | ||||
| manger | 0.4 | 0.3 | 0.29 | .01 | |||
| se révolter | 0.1 | 0.1 | 0.5 | 0.3 |
2.5.3 Mémoire
Par définition, une chaîne de Markov n'a pas de mémoire. Cela n'est pas toujours ce que l'on désire, on voudrait parfois 'ne pas revenir sur ses pas', 'tenir compte de certains éléments clés du passé', … Ceci va être possible, mais va augmenter (potentiellement de façon importante) le nombre d'états.
Imaginons que dans un certain état, on acquière un objet. On aimerait se rappeler que l'on dispose de cet objet. Cela est possible en dédoublant chacun des états en et . Si cela est appliqué à la totalité des états, le nombre d'états a doublé, et le nombre de valeurs dans la table a quadruplé. Cependant, la plupart des valeurs sont identiques à celles que l'on avait précédemment : à moins de poser l'objet, on passe toujours d'un état à un état , et réciproquement, à moins de ramasser l'objet, on passe d'un état à un état [il y a de plus beaucoup de chances que ces deux transitions aient la même valeur numérique]. Les seules valeurs nouvelles correspondent aux actions qui font gagner ou perdre l'objet (transitions de la forme vers ou réciproquement). L'explosion combinatoire peut être un frein à l'utilisation de cette méthode (avec 10 drapeaux, on multiplie le nombre d'états par 1024 et la taille de la table par plus d'un million), mais il est possible de rendre cette explosion quasi négligeable, mais au prix d'une complexité accrue des codes et structures de données.
De la même façon, il est possible de se 'rappeler' de ce qui a été fait à la date précédente, en choisissant comme états non plus mais des couples . Il est à noter que beaucoup de cases de la matrice valent 0, car on ne peut transiter de l'état vers l'état que si (ils correspondent à l'état du système à la même date). Dans la pratique, dans cette éventualité, il est certainement préférable de ne pas conserver dans les cases évidement inutiles.
Dans l'exemple précédent, si on voulait modifier le comportement par "si avant de se révolter, on était en train de dormir, alors il n'y a aucune chance que l'on retourne dormir", on pourrait alors avoir comme table de transition :
| dormir 1 | dormir 2 | dormir 3 | dormir 4 | jouer | manger | dormir -> se révolter | ( "dormir") -> se révolter | |
|---|---|---|---|---|---|---|---|---|
| dormir 1 | 1 | |||||||
| dormir 2 | 1 | |||||||
| dormir 3 | 0.2 | 0.3 | 0.3 | 0.15 | 0.05 | |||
| dormir 4 | 0.1 | 0.4 | 0.45 | 0.05 | ||||
| jouer | 0.4 | 0.4 | 0.2 | |||||
| manger | 0.4 | 0.3 | 0.29 | |||||
| ( "dormir") -> se révolter | 0.1 | 0.1 | 0.5 | 0.3 |
3 SDL2
3.1 Préliminaire
Vous avez déjà eu un aperçu de la SDL2 pendant les cours de C, ne vous privez pas d'y retourner : flood-it.
Le perfectionnement sur cette bibliothèque se fera en réalisant de petits exercices qui mettront en œuvre des outils que vous développerez. Il est intéressant de construire un code propre qui sera le plus facile possible à maintenir et réutiliser. Des mini applications vous serviront de tests fonctionnels, afin de vérifier l'utilisabilité pratique de vos codes.
Les explications qui suivent ne se substituent absolument pas à la consultation de la documentation du wiki, mais pourront vous aider à mettre le pied à l'étrier.

Figure 3 : Logo Simple DirectMedia Layer
Votre première tâche consiste à découvrir la SDL2. Vous devez démontrer au fur et à mesure des exercices que vous savez :
- Afficher une image qui servira de fond,
- Incruster une image (sprite), en gérant la transparence,
- Déplacer le sprite selon les appuis de touche de l'utilisateur, gérer la souris,
- Déplacer le sprite selon une trajectoire fournie par une fonction,
- Tracer des dessins.
Points importants pour la suite
- Chargement propre des composants utiles de la SDL2,
- Libération de la mémoire,
- Travail modulaire afin de favoriser la ré-utilisabilité.
3.2 Installation de la SDL
- Installer la bibliothèque SDL2 :
libsdl2-dev, à laquelle il faudra vraisemblablement ajouter des modules complémentaires, comme la gestion su son, des déformations d'image, réseau, etc… (installer toutlibsdl2-*est, je pense, la bonne solution). - Afin de vérifier la bonne installation, recopier le code suivant qui charge la bibliothèque et affiche le numéro de version
#include <SDL2/SDL.h> #include <stdio.h> /********************************************/ /* Vérification de l'installation de la SDL */ /********************************************/ int main(int argc, char **argv) { (void)argc; (void)argv; SDL_version nb; SDL_VERSION(&nb); printf("Version de la SDL : %d.%d.%d\n", nb.major, nb.minor, nb.patch); return 0; }
Pour compiler/linker ce programme, il est nécessaire d'inclure les bibliothèques nécessaires : gcc verif_SDL.c -o
verif_SDL $(sdl2-config --cflags --libs) (ou gcc verif_SDL.c -o verif_SDL -lSDL2 [auxquels vous ajouterez les
drapeaux habituels -Wall -Wextra et vraisemblablement ~-0g -g~]. L'exécution de sdl2-config avec les options
voulues permet de ne pas indiquer 'à la main' les options, mais de faire appel à un script qui choisit les options,
en particulier en les adaptant selon le système d'exploitation.
3.3 Première fenêtre
La création d'une première fenêtre va se faire en plusieurs étapes
- Initialisation des modes utilisables par la suite (vidéo, son, vibrations, …) via
SDL_Init[il sera possible d'activer par la suite d'autres modules si nécessaire par d'autres fonctions d'initialisation plus spécifiques],- Création de la fenêtre : la fenêtre est le conteneur dans lequel on placera des éléments par la suite. Une
bonne représentation mentale pour faire la distinction avec d'autres éléments qui suivront, est de penser la
fenêtre comme la partie qui interagit avec l'interface graphique du système. La fonction de création d'une
fenêtre est
SDL_CreateWindow. Ses arguments permettent de choisir- son titre
- sa position à la création
- ses dimensions
- plein écran / maximisée / réduite
- visible / cachée
- …
- Libérer le pointeur sur la fenêtre,
- Création de la fenêtre : la fenêtre est le conteneur dans lequel on placera des éléments par la suite. Une
bonne représentation mentale pour faire la distinction avec d'autres éléments qui suivront, est de penser la
fenêtre comme la partie qui interagit avec l'interface graphique du système. La fonction de création d'une
fenêtre est
- Fermer l'utilisation de la SDL
SDL_Quit
#include <SDL2/SDL.h> #include <stdio.h> /************************************/ /* exemple de création de fenêtres */ /************************************/ int main(int argc, char **argv) { (void)argc; (void)argv; SDL_Window *window_1 = NULL, // Future fenêtre de gauche *window_2 = NULL; // Future fenêtre de droite /* Initialisation de la SDL + gestion de l'échec possible */ if (SDL_Init(SDL_INIT_VIDEO) != 0) { SDL_Log("Error : SDL initialisation - %s\n", SDL_GetError()); // l'initialisation de la SDL a échoué exit(EXIT_FAILURE); } /* Création de la fenêtre de gauche */ window_1 = SDL_CreateWindow( "Fenêtre à gauche", // codage en utf8, donc accents possibles 0, 0, // coin haut gauche en haut gauche de l'écran 400, 300, // largeur = 400, hauteur = 300 SDL_WINDOW_RESIZABLE); // redimensionnable if (window_1 == NULL) { SDL_Log("Error : SDL window 1 creation - %s\n", SDL_GetError()); // échec de la création de la fenêtre SDL_Quit(); // On referme la SDL exit(EXIT_FAILURE); } /* Création de la fenêtre de droite */ window_2 = SDL_CreateWindow( "Fenêtre à droite", // codage en utf8, donc accents possibles 400, 0, // à droite de la fenêtre de gauche 500, 300, // largeur = 500, hauteur = 300 0); if (window_2 == NULL) { /* L'init de la SDL : OK fenêtre 1 :OK fenêtre 2 : échec */ SDL_Log("Error : SDL window 2 creation - %s\n", SDL_GetError()); // échec de la création de la deuxième fenêtre SDL_DestroyWindow(window_1); // la première fenétre (qui elle a été créée) doit être détruite SDL_Quit(); exit(EXIT_FAILURE); } /* Normalement, on devrait ici remplir les fenêtres... */ SDL_Delay(2000); // Pause exprimée en ms /* et on referme tout ce qu'on a ouvert en ordre inverse de la création */ SDL_DestroyWindow(window_2); // la fenêtre 2 SDL_DestroyWindow(window_1); // la fenêtre 1 SDL_Quit(); // la SDL return 0; }
3.4 Les évènements
La logique de la gestion des évènements avec la SDL est celle de la boucle évènementielle. C'est une boucle 'infinie', où à chaque tour de boucle, on examine le contenu du buffer clavier, l'état de la souris, on fait évoluer les objets graphiques de quelques pixels, on produit ou on arrête un son… Chaque tour de boucle doit être assez court afin de donner l'illusion que les réactions du programme sont 'instantanées' et que tout se passe en même temps. Pendant une itération il est en général opportun de :
- gérer les affichages,
- examiner certaines entrés (mais avec des commandes non bloquantes, contrairement à
scanfou assimilés), c'est le point principal de la gestion d'évènements, - calculer les nouveaux états,
- faire les pauses nécessaires afin d'obtenir une bonne fluidité (il vaut mieux être globalement un peu lent plutôt que saccadé).
La boucle des évènements suit le squelette suivant:
SDL_bool program_on = SDL_TRUE; // Booléen pour dire que le programme doit continuer SDL_Event event; // c'est le type IMPORTANT !! while (program_on){ // Voilà la boucle des évènements if (SDL_PollEvent(&event)){ // si la file d'évènements n'est pas vide : défiler l'élément en tête // de file dans 'event' switch(event.type){ // En fonction de la valeur du type de cet évènement case SDL_QUIT : // Un évènement simple, on a cliqué sur la x de la fenêtre program_on = SDL_FALSE; // Il est temps d'arrêter le programme break; default: // L'évènement défilé ne nous intéresse pas break; } } // Affichages et calculs souvent ici }
La page SDL_Event liste les valeurs possibles que peut prendre dans le code précédent la variable
event.type. event est une structure qui contient une union. Ainsi, on peut accéder au champ type de cette
structure, et selon la valeur du type, on peut accéder à ce qui est pertinent pour ce type, qui se trouve dans
l'union. Cette façon de ranger peut vous inspirer lorsque vous avez à conserver des éléments qui ont des rôles
similaires mais qui peuvent prendre des formes différentes.
La boucle d'évènement peut être un peu étoffée :
SDL_bool program_on = SDL_TRUE, // Booléen pour dire que le programme doit continuer paused = SDL_FALSE; // Booléen pour dire que le programme est en pause SDL_Event event; // Evènement à traiter while (program_on) { // La boucle des évènements if(SDL_PollEvent(&event)) { // Tant que la file des évènements stockés n'est pas vide et qu'on n'a pas // terminé le programme Défiler l'élément en tête de file dans 'event' switch (event.type) { // En fonction de la valeur du type de cet évènement case SDL_QUIT: // Un évènement simple, on a cliqué sur la x de la // fenêtre program_on = SDL_FALSE; // Il est temps d'arrêter le programme break; case SDL_KEYDOWN: // Le type de event est : une touche appuyée // comme la valeur du type est SDL_Keydown, dans la partie 'union' de // l'event, plusieurs champs deviennent pertinents switch (event.key.keysym.sym) { // la touche appuyée est ... case SDLK_p: // 'p' case SDLK_SPACE: // ou 'SPC' paused = !paused; // basculement pause/unpause break; case SDLK_ESCAPE: // 'ESCAPE' case SDLK_q: // ou 'q' program_on = 0; // 'escape' ou 'q', d'autres façons de quitter le programme break; default: // Une touche appuyée qu'on ne traite pas break; } break; case SDL_MOUSEBUTTONDOWN: // Click souris if (SDL_GetMouseState(NULL, NULL) & SDL_BUTTON(SDL_BUTTON_LEFT) ) { // Si c'est un click gauche change_state(state, 1, window); // Fonction à éxécuter lors d'un click gauche } else if (SDL_GetMouseState(NULL, NULL) & SDL_BUTTON(SDL_BUTTON_RIGHT) ) { // Si c'est un click droit change_state(state, 2, window); // Fonction à éxécuter lors d'un click droit } break; default: // Les évènements qu'on n'a pas envisagé break; } } draw(state, &color, renderer, window); // On redessine if (!paused) { // Si on n'est pas en pause next_state(state, survive, born); // la vie continue... } SDL_Delay(50); // Petite pause }
3.5 Travail à réaliser : un X fenêtré

Figure 4 : X-Men (affiche film dark phoenix)
Vous devez mettre en évidence par un code votre aptitude à ouvrir et fermer des fenêtres. Un résultat possible de votre travail pourrait être : ./all_executables.tar.gz (télécharger, exécuter 'X_fenetre'). N'hésitez pas à demander à un enseignant si ce que vous vous proposez de réaliser correspond à la difficulté recherchée.
Remarques :
- la fonction
void SDL_SetWindowPosition(SDL_Window * window, int x, int y)permet de positionner une fenêtre, - la fonction
void SDL_GetWindowPosition(SDL_Window * window,int *x, int *y)permet de récupérer la position d'une fenêtre, - la fonction
void SDL_GetWindowSize(SDL_Window * window, int *w, int *h)permet de récupérer les dimensions d'une fenêtre, - la fonction
int SDL_GetCurrentDisplayMode(int displayIndex, SDL_DisplayMode * mode)permet de récupérer les dimensions de l'écran.
3.6 Mettre un 'rendu' dans une fenêtre
Un rendu/renderer est une zone dans laquelle il sera possible de dessiner ou de poser des images. Un rendu se 'dépose' dans une fenêtre, on peut l'imaginer comme une toile que l'on placerait sur un chevalet (le chevalet étant la fenêtre), cette toile étant munie de tout l'équipement qui permet de la peindre. La fenêtre crée un lien avec l'interface graphique du système, le rendu un lien entre la fenêtre et ce qu'on y affiche. Par la suite on apprendra à peindre la toile, ou à y coller des images.
D'un point de vue plus technique, le rendu va nous permettre de définir quelles fonctions vont être utilisées pour réaliser la visualisation (utilisation ou non des accélérations de la carte graphique et autres options connues des utilisateurs de jeux vidéo telles que l'activation de la synchronisation verticale, etc…). Le rendu est alors pensé comme un moteur d'affichage.
Pour créer un rendu on utilise la fonction SDL_CreateRender, et pour le détruire SDL_DestroyRenderer. Une fois un
rendu créé (ou par la suite modifié), il est nécessaire de réaliser son affichage, fonction SDL_RenderPresent. Dans
l'éventualité où on désire effacer un rendu, on utilise la fonction SDL_RenderClear, qui va 'repeindre' la surface
par une couleur de notre choix (noir par défaut).
3.7 Dessiner sur un rendu
Pour dessiner sur le renderer, on peut par exemple :
- tracer un point
SDL_RenderDrawPoint - tracer une ligne
SDL_RenderDrawLine - tracer un rectangle
SDL_RenderDrawRectangle - tracer un rectangle plein
SDL_RenderFillRect - changer de couleur
SDL_RenderDrawColor
Il existe également des variantes de ces fonctions permettant de tracer en une seule commande plusieurs points, plusieurs lignes, etc…
#include <SDL2/SDL.h> #include <math.h> #include <stdio.h> #include <string.h> /*********************************************************************************************************************/ /* Programme d'exemple de création de rendu + dessin */ /*********************************************************************************************************************/ void end_sdl(char ok, // fin normale : ok = 0 ; anormale ok = 1 char const* msg, // message à afficher SDL_Window* window, // fenêtre à fermer SDL_Renderer* renderer) { // renderer à fermer char msg_formated[255]; int l; if (!ok) { // Affichage de ce qui ne va pas strncpy(msg_formated, msg, 250); l = strlen(msg_formated); strcpy(msg_formated + l, " : %s\n"); SDL_Log(msg_formated, SDL_GetError()); } if (renderer != NULL) { // Destruction si nécessaire du renderer SDL_DestroyRenderer(renderer); // Attention : on suppose que les NULL sont maintenus !! renderer = NULL; } if (window != NULL) { // Destruction si nécessaire de la fenêtre SDL_DestroyWindow(window); // Attention : on suppose que les NULL sont maintenus !! window= NULL; } SDL_Quit(); if (!ok) { // On quitte si cela ne va pas exit(EXIT_FAILURE); } } void draw(SDL_Renderer* renderer) { // Je pense que vous allez faire moins laid :) SDL_Rect rectangle; SDL_SetRenderDrawColor(renderer, 50, 0, 0, // mode Red, Green, Blue (tous dans 0..255) 255); // 0 = transparent ; 255 = opaque rectangle.x = 0; // x haut gauche du rectangle rectangle.y = 0; // y haut gauche du rectangle rectangle.w = 400; // sa largeur (w = width) rectangle.h = 400; // sa hauteur (h = height) SDL_RenderFillRect(renderer, &rectangle); SDL_SetRenderDrawColor(renderer, 0, 0, 0, 255); SDL_RenderDrawLine(renderer, 0, 0, // x,y du point de la première extrémité 400, 400); // x,y seconde extrémité /* tracer un cercle n'est en fait pas trivial, voilà le résultat sans algo intelligent ... */ for (float angle = 0; angle < 2 * M_PI; angle += M_PI / 4000) { SDL_SetRenderDrawColor(renderer, (cos(angle * 2) + 1) * 255 / 2, // quantité de Rouge (cos(angle * 5) + 1) * 255 / 2, // de vert (cos(angle) + 1) * 255 / 2, // de bleu 255); // opacité = opaque SDL_RenderDrawPoint(renderer, 200 + 100 * cos(angle), // coordonnée en x 200 + 150 * sin(angle)); // en y } } int main(int argc, char** argv) { (void)argc; (void)argv; SDL_Window* window = NULL; SDL_Renderer* renderer = NULL; SDL_DisplayMode screen; /*********************************************************************************************************************/ /* Initialisation de la SDL + gestion de l'échec possible */ if (SDL_Init(SDL_INIT_VIDEO) != 0) end_sdl(0, "ERROR SDL INIT", window, renderer); SDL_GetCurrentDisplayMode(0, &screen); printf("Résolution écran\n\tw : %d\n\th : %d\n", screen.w, screen.h); /* Création de la fenêtre */ window = SDL_CreateWindow("Premier dessin", SDL_WINDOWPOS_CENTERED, SDL_WINDOWPOS_CENTERED, screen.w * 0.66, screen.h * 0.66, SDL_WINDOW_OPENGL); if (window == NULL) end_sdl(0, "ERROR WINDOW CREATION", window, renderer); /* Création du renderer */ renderer = SDL_CreateRenderer(window, -1, SDL_RENDERER_ACCELERATED | SDL_RENDERER_PRESENTVSYNC); if (renderer == NULL) end_sdl(0, "ERROR RENDERER CREATION", window, renderer); /*********************************************************************************************************************/ /* On dessine dans le renderer */ /*********************************************************************************************************************/ /* Cette partie pourrait avantageusement être remplacée par la boucle évènementielle */ draw(renderer); // appel de la fonction qui crée l'image SDL_RenderPresent(renderer); // affichage SDL_Delay(1000); // Pause exprimée en ms /* on referme proprement la SDL */ end_sdl(1, "Normal ending", window, renderer); return EXIT_SUCCESS; }
- Remarques
- Une fonction de terminaison
end_sdlassez brutale est apparue (il y a desexitalors que ce n'est pas lemain!), à vous de voir comment gérer au mieux les erreurs avec la SDL… en attendant la ZZ2 pour avoir un mécanisme propre de gestion des exceptions en c++. Pour apprendre à tracer des cercles, et en général à faire du dessin sur ordinateur, ma référence reste l'ouvrage de Michael Abrash Zen de la programmation graphique / Graphics programing handbook dont je vous recommande la lecture.
- Une fonction de terminaison
3.8 Travail à réaliser : pavé de serpents
Le but est ici de démontrer vos talents pour réaliser une animation uniquement basée sur des tracés de figures simples. Une réalisation possible serait ./all_executables.tar.gz (télécharger, exécuter 'snake').
- Remarques
- après avoir dessiné quelque chose, il faut penser à l'afficher en utilisant
void SDL_RenderPresent(SDL_Renderer * renderer)suivi d'unvoid SDL_Delay(Uint32 ms)d'au moins (environ) 10ms. - Si on désire effacer la fenêtre avec
int SDL_RenderClear(SDL_Renderer * renderer), il faut préalablement avoir choisi avecint SDL_SetRenderDrawColor(SDL_Renderer * renderer,Uint8 r, Uint8 g, Uint8 b, Uint8 a)la couleur dans laquelle le fond devra être peint.
- après avoir dessiné quelque chose, il faut penser à l'afficher en utilisant
3.9 Travail à réaliser : jeu de la vie

Pour mettre en évidence votre maitrise du dessin, vous allez coder un Jeu de la vie (ou par Etienne Ghys).Votre programme devra proposer deux formes de monde:
- monde délimité : la grille du monde possède un bord [Cette version a pour but de vous permettre de générer
rapidement un labyrinthe en utilisant les bonnes règles de transition.]
- celui-ci peut être ajouté au début et ne pas pouvoir être modifié (cellules immortelles)
- ou après l'exécution, auquel cas on se contentera de faire disparaître toute cellule vivante qui est hors grille) et on ajoute le bord une fois l'exécution terminée.
- monde torique : la grille possède la forme d'un tore (anneau), c'est à dire que la case à droite d'une case du bord droit sera la case à gauche de la même ligne (et inversement), et la case en haut d'une case du bord haut sera la case en bas de la même colonne (et inversement).
Les règles d'évolution du jeu de la vie doivent être codées en utilisant deux tableaux de 9 booléens qui permettent de stocker les règles particulières de ce jeu de la vie (règles alternatives) :
- tableau 'survie' : si la cellule en cours d'examen est vivante et
survie[nb_voisins_vivants] == Faux, alors la cellule meurt, - tableau 'naissance' : si la cellule en cours d'examen est morte et
naissance[nb_voisins_vivants] == Vrai, alors la cellule naît. - La configuration initiale sera entrée par l'utilisateur à la souris,
- il doit être possible de sauvegarder / charger une configuration,
- avec les flèches du clavier il doit être possible d'accélérer / freiner l'animation,
- il doit être aisé par une modification très rapide du code de changer les règles de transition,
- il doit y avoir une détection de 'l'état est stable' qui affiche un message,
- [optionnel] un redimensionnement pendant le fonctionnement de la grille (zoom avant/arrière) peut être géré,
- [optionnel] une détection de cycle peut être effectuée (une situation passée est revenue).
3.10 Manipuler des textures
Une texture est une structure qui peut contenir une image, ainsi que les informations largeur et hauteur de l'image.
3.10.1 Chargement d'une image
La création d'une texture commence fréquemment par le chargement d'une image. Pour cela, la procédure la plus classique consiste à repasser temporairement en SDL1 :
- on crée une surface (type de données SDL1)
- on charge l'image dans la SDL_Surface,
- on transforme la surface en texture (type de données correspondant en SDL2)
- Remarque
- la SDL ne fonctionne par défaut qu'avec le format bmp… Afin de pouvoir
utiliser d'autres formats, il est nécessaire d'ajouter une bibliothèque
#include <SDL2/SDL_image.h>. Il sera alors nécessaire de compiler avec le drapeau-lSDL2_image.
#include <SDL2/SDL_image.h>
- la SDL ne fonctionne par défaut qu'avec le format bmp… Afin de pouvoir
utiliser d'autres formats, il est nécessaire d'ajouter une bibliothèque
On peut écrire une fonction qui charge une image dans une texture :
#include <SDL2/SDL_image.h> // Nécessaire pour la fonction IMG_Load // Penser au flag -lsdl2_image à la compilation //... SDL_Texture* load_texture_from_image(char * file_image_name, SDL_Window *window, SDL_Renderer *renderer ){ SDL_Surface *my_image = NULL; // Variable de passage SDL_Texture* my_texture = NULL; // La texture my_image = IMG_Load(file_image_name); // Chargement de l'image dans la surface // image=SDL_LoadBMP(file_image_name); fonction standard de la SDL, // uniquement possible si l'image est au format bmp */ if (my_image == NULL) end_sdl(0, "Chargement de l'image impossible", window, renderer); my_texture = SDL_CreateTextureFromSurface(renderer, my_image); // Chargement de l'image de la surface vers la texture SDL_FreeSurface(my_image); // la SDL_Surface ne sert que comme élément transitoire if (my_texture == NULL) end_sdl(0, "Echec de la transformation de la surface en texture", window, renderer); return my_texture; } //... IMG_Quit() // Si on charge une librairie SDL, il faut penser à la décharger
Remarque :
- le paramètre
SDL_Window *windowne sert qu'en cas de problème à fermer la fenêtre,
On peut préférer à cette méthode 'traditionnelle' :
#include <SDL2/SDL_image.h> // ... SDL_Texture *my_texture; my_texture = IMG_LoadTexture(renderer,"./img/Maze.png"); if (my_texture == NULL) end_sdl(0, "Echec du chargement de l'image dans la texture", window, renderer); //... IMG_Quit()
Dans tous les cas, il ne faut alors pas oublier la contrepartie à la création d'une texture : sa libération…
SDL_DestroyTexture(my_texture);
3.10.2 Affichage d'une texture sur la totalité de la fenêtre
Une fois une texture créée, on peut désirer l'afficher, c'est la fonction SDL_RenderCopy
qui va copier la texture, ou une partie de la texture à l'endroit indiqué dans
le renderer.
void play_with_texture_1(SDL_Texture *my_texture, SDL_Window *window, SDL_Renderer *renderer) { SDL_Rect source = {0}, // Rectangle définissant la zone de la texture à récupérer window_dimensions = {0}, // Rectangle définissant la fenêtre, on n'utilisera que largeur et hauteur destination = {0}; // Rectangle définissant où la zone_source doit être déposée dans le renderer SDL_GetWindowSize( window, &window_dimensions.w, &window_dimensions.h); // Récupération des dimensions de la fenêtre SDL_QueryTexture(my_texture, NULL, NULL, &source.w, &source.h); // Récupération des dimensions de l'image destination = window_dimensions; // On fixe les dimensions de l'affichage à celles de la fenêtre /* On veut afficher la texture de façon à ce que l'image occupe la totalité de la fenêtre */ SDL_RenderCopy(renderer, my_texture, &source, &destination); // Création de l'élément à afficher SDL_RenderPresent(renderer); // Affichage SDL_Delay(2000); // Pause en ms SDL_RenderClear(renderer); // Effacer la fenêtre }
Remarque :
- Il ne faut pas oublier d'afficher avec
SDL_RenderPresentet de mettre une pauseSDL_Delaysi on espère voir quelque chose.
3.10.3 Affichage d'une partie d'une texture à un endroit choisi
void play_with_texture_2(SDL_Texture* my_texture, SDL_Window* window, SDL_Renderer* renderer) { SDL_Rect source = {0}, // Rectangle définissant la zone de la texture à récupérer window_dimensions = {0}, // Rectangle définissant la fenêtre, on n'utilisera que largeur et hauteur destination = {0}; // Rectangle définissant où la zone_source doit être déposée dans le renderer SDL_GetWindowSize( window, &window_dimensions.w, &window_dimensions.h); // Récupération des dimensions de la fenêtre SDL_QueryTexture(my_texture, NULL, NULL, &source.w, &source.h); // Récupération des dimensions de l'image float zoom = 1.5; // Facteur de zoom à appliquer destination.w = source.w * zoom; // La destination est un zoom de la source destination.h = source.h * zoom; // La destination est un zoom de la source destination.x = (window_dimensions.w - destination.w) /2; // La destination est au milieu de la largeur de la fenêtre destination.y = (window_dimensions.h - destination.h) / 2; // La destination est au milieu de la hauteur de la fenêtre SDL_RenderCopy(renderer, my_texture, // Préparation de l'affichage &source, &destination); SDL_RenderPresent(renderer); SDL_Delay(1000); SDL_RenderClear(renderer); // Effacer la fenêtre }
Remarque
- Ici, la source a pris la totalité de la texture, en modifiant les quatre
paramètres du rectangle
source, il aurait été possible de n'en prendre qu'une partie (obligatoirement rectangulaire).
3.10.4 Créer une première animation
L'idée ici est de déposer successivement la texture à différents endroits de l'écran, en effaçant l'écran entre chaque affichage.
void play_with_texture_3(SDL_Texture* my_texture, SDL_Window* window, SDL_Renderer* renderer) { SDL_Rect source = {0}, // Rectangle définissant la zone de la texture à récupérer window_dimensions = {0}, // Rectangle définissant la fenêtre, on n'utilisera que largeur et hauteur destination = {0}; // Rectangle définissant où la zone_source doit être déposée dans le renderer SDL_GetWindowSize( window, &window_dimensions.w, &window_dimensions.h); // Récupération des dimensions de la fenêtre SDL_QueryTexture(my_texture, NULL, NULL, &source.w, &source.h); // Récupération des dimensions de l'image /* On décide de déplacer dans la fenêtre cette image */ float zoom = 0.25; // Facteur de zoom entre l'image source et l'image affichée int nb_it = 200; // Nombre d'images de l'animation destination.w = source.w * zoom; // On applique le zoom sur la largeur destination.h = source.h * zoom; // On applique le zoom sur la hauteur destination.x = (window_dimensions.w - destination.w) / 2; // On centre en largeur float h = window_dimensions.h - destination.h; // hauteur du déplacement à effectuer for (int i = 0; i < nb_it; ++i) { destination.y = h * (1 - exp(-5.0 * i / nb_it) / 2 * (1 + cos(10.0 * i / nb_it * 2 * M_PI))); // hauteur en fonction du numéro d'image SDL_RenderClear(renderer); // Effacer l'image précédente SDL_SetTextureAlphaMod(my_texture,(1.0-1.0*i/nb_it)*255); // L'opacité va passer de 255 à 0 au fil de l'animation SDL_RenderCopy(renderer, my_texture, &source, &destination); // Préparation de l'affichage SDL_RenderPresent(renderer); // Affichage de la nouvelle image SDL_Delay(30); // Pause en ms } SDL_RenderClear(renderer); // Effacer la fenêtre une fois le travail terminé }
Remarque :
- il y a un fade-out dans cette animation : l'objet disparait petit à petit à la fin de l'animation. Pour obtenir ce résultat, SDL_SetTextureAlphaMod est utilisée. Cette fonction permet d'appliquer un coefficient de transparence à une texture (0 pour invisible, 255 pour opaque). S'il y avait un fond, il serait plus ou moins visible en fonction de la transparence choisie.
3.10.5 Et si on veut animer un 'sprite' ?
Les planches des sprites utilisées dans les animations sont construites en positionnant un objet dans ces différentes positions dans une même image (on peut appeler ces positions des vignettes). Il est important que :
- les positions soient placées intelligemment dans l'image : les vignettes sont si possible de la même taille,
espacées régulièrement. L'objectif est de permettre de parcourir séquentiellement aisément les différentes vignettes
qui constituent l'animation en déplaçant le rectangle
sourcesur l'image de façon régulière, - le fond de l'image soit transparent : sur les formats type png un point est codé par 4 valeurs (de 0 à 255)
. Cette dernière composante est à 0 pour une parfaite transparence, et à 255 pour
une parfaite opacité. Il est aisé d'incorporer des sprites dont le fond est transparent à n'importe quel
décor. Dans l'éventualité où le fond du sprite serait uni, il y a plusieurs possibilités :
- reprendre l'image avec un logiciel de dessin (gimp par exemple, présent sur la plupart des système Linux), l'outil permet même de réaliser un détourage avec un dégradé de transparence sur le bord du sujet afin qu'il se fonde au mieux dans n'importe quel décor,
- utiliser des fonctions de la SDL qui permettent de choisir une ou plusieurs couleurs comme étant en réalité transparentes (c'est souvent ce que l'on fait avec des images au format bmp qui ne gèrent pas dans leur format la transparence),
- utiliser un masque de transparence : on crée une image supplémentaire, en intensité de gris qui va servir, de façon totalement similaire à la 4ième composante du png, à indiquer la transparence. Cette méthode, peut également donner des résultats intéressants pour créer des effets (par exemple une lampe torche qui se déplace en utilisant un disque avec un dégradé radial au bord que l'on déplace sur une image : sur la partie peinte à 100% du disque, on voit l'image, sur la partie peinte à 0%; on ne voit rien, et entre les deux une zone en clair obscur).
Vous pourrez par exemple utiliser vignettes libres kenney, ou celles-ci, ou rechercher par vous-même une planche sur votre moteur de recherche préféré "free tileset dungeon" (se limiter aux planches libres de droit !!).
void play_with_texture_4(SDL_Texture* my_texture, SDL_Window* window, SDL_Renderer* renderer) { SDL_Rect source = {0}, // Rectangle définissant la zone totale de la planche window_dimensions = {0}, // Rectangle définissant la fenêtre, on n'utilisera que largeur et hauteur destination = {0}, // Rectangle définissant où la zone_source doit être déposée dans le renderer state = {0}; // Rectangle de la vignette en cours dans la planche SDL_GetWindowSize(window, // Récupération des dimensions de la fenêtre &window_dimensions.w, &window_dimensions.h); SDL_QueryTexture(my_texture, // Récupération des dimensions de l'image NULL, NULL, &source.w, &source.h); /* Mais pourquoi prendre la totalité de l'image, on peut n'en afficher qu'un morceau, et changer de morceau :-) */ int nb_images = 8; // Il y a 8 vignette dans la ligne de l'image qui nous intéresse float zoom = 2; // zoom, car ces images sont un peu petites int offset_x = source.w / nb_images, // La largeur d'une vignette de l'image, marche car la planche est bien réglée offset_y = source.h / 4; // La hauteur d'une vignette de l'image, marche car la planche est bien réglée state.x = 0 ; // La première vignette est en début de ligne state.y = 3 * offset_y; // On s'intéresse à la 4ème ligne, le bonhomme qui court state.w = offset_x; // Largeur de la vignette state.h = offset_y; // Hauteur de la vignette destination.w = offset_x * zoom; // Largeur du sprite à l'écran destination.h = offset_y * zoom; // Hauteur du sprite à l'écran destination.y = // La course se fait en milieu d'écran (en vertical) (window_dimensions.h - destination.h) /2; int speed = 9; for (int x = 0; x < window_dimensions.w - destination.w; x += speed) { destination.x = x; // Position en x pour l'affichage du sprite state.x += offset_x; // On passe à la vignette suivante dans l'image state.x %= source.w; // La vignette qui suit celle de fin de ligne est // celle de début de ligne SDL_RenderClear(renderer); // Effacer l'image précédente avant de dessiner la nouvelle SDL_RenderCopy(renderer, my_texture, // Préparation de l'affichage &state, &destination); SDL_RenderPresent(renderer); // Affichage SDL_Delay(80); // Pause en ms } SDL_RenderClear(renderer); // Effacer la fenêtre avant de rendre la main }
3.10.6 Et le fond ?
Fréquemment, on désire incruster un sprite sur un décor, et non sur un fond uni. Pour afficher, cela ne pose pas de problème particulier : à la façon d'un peintre, on positionne successivement les couches, et ce qui est peint après cache ce qui a été peint précédemment (superposition des couches).
Pour ce qui est de l'effacement, on peut effacer toute l'image, puis recommencer la totalité de la peinture (peut-être après avoir sauvegardé le fond, en particulier s'il est procédural). Cette solution est utilisée en particulier sur les jeux où il y a un scrolling de l'écran, et dans le cas général lorsque le 'fond' varie sur une grande partie.
Lorsque entre chaque image peu de choses ont été modifiées, on peut préférer sauvegarder un rectangle de fond qui englobe l'endroit où sera positionné l'élément mobile, superposer au fond l'élément mobile, afficher, et avant de passer à l'image suivante recopier la sauvegarde du fond pour effacer l'élément mobile. L'avantage de cette méthode est (potentiellement) sa vitesse car on ne modifie qu'une partie de la texture à afficher et pas sa totalité. Elle est moins utilisée maintenant suite à l'évolution des performances des circuits graphiques, et on préfère souvent simplifier le code, cette optimisation n'étant plus réellement nécessaire…
void play_with_texture_5(SDL_Texture *bg_texture, SDL_Texture *my_texture, SDL_Window *window, SDL_Renderer *renderer) { SDL_Rect source = {0}, // Rectangle définissant la zone de la texture à récupérer window_dimensions = {0}, // Rectangle définissant la fenêtre, on n'utilisera que largeur et hauteur destination = {0}; // Rectangle définissant où la zone_source doit être déposée dans le renderer SDL_GetWindowSize(window, // Récupération des dimensions de la fenêtre &window_dimensions.w, &window_dimensions.h); SDL_QueryTexture(my_texture, NULL, NULL, // Récupération des dimensions de l'image &source.w, &source.h); int nb_images = 40; // Il y a 8 vignette dans la ligne qui nous intéresse int nb_images_animation = 1 * nb_images; // float zoom = 2; // zoom, car ces images sont un peu petites int offset_x = source.w / 4, // La largeur d'une vignette de l'image offset_y = source.h / 5; // La hauteur d'une vignette de l'image SDL_Rect state[40]; // Tableau qui stocke les vignettes dans le bon ordre pour l'animation /* construction des différents rectangles autour de chacune des vignettes de la planche */ int i = 0; for (int y = 0; y < source.h ; y += offset_y) { for (int x = 0; x < source.w; x += offset_x) { state[i].x = x; state[i].y = y; state[i].w = offset_x; state[i].h = offset_y; ++i; } } // ivaut 20 en sortie de boucle state[15] = state[14] // on fabrique des images 14 et 15 en reprenant la 13 = state[13]; // donc state[13 à 15] ont la même image, le monstre ne bouge pas for(; i< nb_images ; ++i){ // reprise du début de l'animation en sens inverse state[i] = state[39-i]; // 20 == 19 ; 21 == 18 ; ... 39 == 0 } destination.w = offset_x * zoom; // Largeur du sprite à l'écran destination.h = offset_y * zoom; // Hauteur du sprite à l'écran destination.x = window_dimensions.w * 0.75; // Position en x pour l'affichage du sprite destination.y = window_dimensions.h * 0.7; // Position en y pour l'affichage du sprite i = 0; for (int cpt = 0; cpt < nb_images_amination ; ++cpt) { play_with_texture_1_1(bg_texture, // identique à play_with_texture_1, où on a enlevé l'affichage et la pause window, renderer); SDL_RenderCopy(renderer, // Préparation de l'affichage my_texture, &state[i], &destination); i = (i + 1) % nb_images; // Passage à l'image suivante, le modulo car l'animation est cyclique SDL_RenderPresent(renderer); // Affichage SDL_Delay(100); // Pause en ms } SDL_RenderClear(renderer); // Effacer la fenêtre avant de rendre la main }
3.10.7 Gestion de la parallaxe

Le défilement parallaxe consiste à donner une impression de profondeur en utilisant plusieurs fonds superposés les uns sur les autres (algorithme du peintre : la nouvelle couche de peinture en recouvrant l'ancienne cache ce qui était dessiné) que l'on anime à des vitesses différentes (ce qui est plus loin bouge plus lentement).
Si on imagine que l'on regarde le paysage depuis une voiture :
- le soleil et la lune, à l'infini, ne bougent pas, on les dessine en premier
- les montagnes à l'horizon ne bougent quasiment pas : on va les dessiner ensuite,
- les collines un peu plus proches se déplacent à une vitesse moyenne,
- les arbres au bord de la route se déplacent à la vitesse de la voiture, comme ils sont les plus proches on les dessine en dernier.
Pour que tout se passe bien, il ne faut pas oublier de gérer la transparence : les arbres ne doivent se dessiner que
là où il y a de la matière. Dans l'image de l'arbre, ce qui n'est pas arbre doit être de couleur totalement
transparente (rappel : les images au format png possèdent un canal α pour gérer la transparence).
On peut encore améliorer l'effet de profondeur en jouant sur les couleurs et la netteté :
- plus un décor est lointain, plus on en diminue la netteté (le flou créé par les l'air)
- plus un décor est lointain, plus on en diminue le contraste.
Afin de réaliser ces effets, on peut utiliser le logiciel gimp, ou tout autre logiciel de traitement d'images prenant en charge ces
éléments (quasiment tous).
3.10.8 Résultat
Si on remet les différents morceaux de code précédents bout-à-bout, et peut-être quelque modifications mineures, on obtient ./all_executables.tar.gz (télécharger, exécuter 'textures').
3.10.9 Travail à réaliser : une animation
Il est temps de mettre en pratique ce que l'on vient de voir sur les textures, en créant une petite animation simple. Il est inutile qu'elle soit paramétrable, il ne faut pas y passer trop longtemps, faites uniquement de petites variations par rapport à ce qui a été proposé ci-avant, gardez vos idées géniales pour la suite :-).
3.11 Écrire à l'écran
La bibliothèque SDL_ttf propose de multiples outils pour écrire et manipuler du texte.
Encore une fois, il faut charger la bibliothèque :
#include <SDL2/SDL_ttf.h>
Et initialiser ses fonctionnalités :
if (TTF_Init() < 0) end_sdl(0, "Couldn't initialize SDL TTF", window, renderer);
Une fois le travail terminé, il ne faudra pas oublier de refermer cette bibliothèque :
TTF_Quit();
Ainsi, on peut obtenir un nouveau 'Hello World!' (télécharger, exécuter 'hello'), en n'oubliant pas
d'ajouter le drapeau -lSDL2_ttf lors de la compilation.
#include <SDL2/SDL_ttf.h> // Charger la bibliothèque ... if (TTF_Init() < 0) end_sdl(0, "Couldn't initialize SDL TTF", window, renderer); TTF_Font* font = NULL; // la variable 'police de caractère' font = TTF_OpenFont("./fonts/Pacifico.ttf", 65); // La police à charger, la taille désirée if (font == NULL) end_sdl(0, "Can't load font", window, renderer); TTF_SetFontStyle(font, TTF_STYLE_ITALIC | TTF_STYLE_BOLD); // en italique, gras SDL_Color color = {20, 0, 40, 255}; // la couleur du texte SDL_Surface* text_surface = NULL; // la surface (uniquement transitoire) text_surface = TTF_RenderText_Blended(font, "Hello World !", color); // création du texte dans la surface if (text_surface == NULL) end_sdl(0, "Can't create text surface", window, renderer); SDL_Texture* text_texture = NULL; // la texture qui contient le texte text_texture = SDL_CreateTextureFromSurface(renderer, text_surface); // transfert de la surface à la texture if (text_texture == NULL) end_sdl(0, "Can't create texture from surface", window, renderer); SDL_FreeSurface(text_surface); // la texture ne sert plus à rien SDL_Rect pos = {0, 0, 0, 0}; // rectangle où le texte va être prositionné SDL_QueryTexture(text_texture, NULL, NULL, &pos.w, &pos.h); // récupération de la taille (w, h) du texte SDL_RenderCopy(renderer, text_texture, NULL, &pos); // Ecriture du texte dans le renderer SDL_DestroyTexture(text_texture); // On n'a plus besoin de la texture avec le texte SDL_RenderPresent(renderer); // Affichage ... TTF_Quit(); // Quitter la bibliothèque ...
La fonction TTF_RenderText_Blended peut être remplacée par deux autres
fonctions selon la vitesse demandée pour afficher et la qualité de la fusion
entre le texte et l'image attendue : documentation
Il existe des fonctions adaptées à l'encodage UTF8 des caractères (au lieu du Latin1) disponibles dans cette bibliothèque.
3.12 Travail à réaliser : un premier chef d’œuvre
Le but ici est de mettre en œuvre tout ce qui a été vu sur la SDL, en créant un mini jeu. Vous pouvez créer une variation autour de space number (télécharger, exécuter 'spacenumber') ou vous pouvez proposer un jeu totalement différent (à faire valider par l'enseignant), en gardant en tête que ce n'est qu'un exercice, et qu'il ne faudrait pas lui accorder plus d'une journée.
Votre jeu devra mettre en œuvre une chaîne de Markov afin de gérer le comportement d'au moins un élément du jeu. De façon simple, cela s'adapte bien au déplacement d'un objet (ennemi par exemple), afin qu'il ait un déplacement 'raisonnable'. Cela pourrait également définir le comportement d'un actant (pensez par exemple aux actions des personnages du jeu Sims).
Voici un exemple dans le contexte de création d'une route, on définit la courbure de la route en fonction de la courbure qu'elle avait au mètre précédent (NB : le temps a été ici remplacé par la position, ce qui ne change évidemment rien).
| tourner de -5 degrés | aller tout droit | tourner de +5 degrés | |
| tourner de -5 degrés | 30% | 70% | |
| aller tout droit | 10% | 80% | 10% |
| tourner de +5 degrés | 70% | 30% |
Qui va donner une route beaucoup moins sinueuse que :
| tourner de -5 degrés | aller tout droit | tourner de +5 degrés | |
| tourner de -5 degrés | 40% | 50% | 10% |
| aller tout droit | 30% | 40% | 30% |
| tourner de +5 degrés | 10% | 50% | 40% |
4 Apprentissage par renforcement
4.1 Problématique
Dans l'apprentissage artificiel il existe plusieurs sous catégories. On va s'intéresser ici à un type d'apprentissage qui se rapproche de la méthode 'essai-erreur' que l'on appelle l'apprentissage par renforcement. Le programme (qui sera par la suite nommé indifféremment agent ou système) réalise une suite d'actions et après un certain laps de temps, on évalue la qualité de l'état atteint. On remonte alors dans la liste des actions réalisées et on augmente leur probabilité de réalisation (si l'évaluation finale a été favorable), ou on la diminue (si elle a été défavorable).

Figure 6 : Méthodologie essai et erreur
4.1.1 Domaines d'applications
On peut ainsi imaginer utiliser (avec plus ou moins de variations par rapport à ce qui est introduit dans ce document) cette méthode dans des situations telles que :
- apprendre à jouer au go : l'ordinateur joue avec deux programmes, lorsqu'un des programmes gagne, on favorise par le futur les coups joués dans les mêmes situations, et inversement s'il perd.
- apprendre à garer une voiture : un environnement est simulé sur ordinateur, le programme réalise des actions (tourner de x degrés à gauche le volant, accélérer, freiner), on évalue la qualité de la position de la voiture après N actions, et on améliore nos connaissances de ce qu'il faut ou il ne faut pas faire. Le pilotage peut aller jusqu'au véhicule autonome, voire même au véhicule de course.
- apprendre à jouer au casse briques : l’ordinateur peut déplacer la raquette à droite ou à gauche, s'il perd la balle, l'évaluation est négative, s'il ne la perd pas, l'évaluation est le temps moyen utilisé afin de toucher une brique (ce qui permettra de favoriser les coups les plus efficaces, et pas seulement de rattraper la balle).
- apprendre à se mouvoir : un robot dispose de différents actionneurs (par exemple : un par articulation), le but est de lui apprendre à les combiner afin qu'il puisse passer d'une position couchée à la position debout.
- …
La méthode abordée ici a pour vocation d'apprendre à un programme à prendre des décisions. Pour cela on simule un environnement analogue à celui qui sera utilisé dans l'application finale, et on génère des actions dans cet environnement (parfois on travaille directement dans l'univers réel, mais ce n'est en général pas la voie privilégiée). L'apprentissage par renforcement consiste à renforcer les comportements qui ont menés à des résultats positifs et à réfréner ceux dont les conséquences ont été néfastes.
- Restriction 1
- La méthode abordée nécessite de simuler l'environnement de façon suffisamment pertinente pour permettre la transposition de ce qui a été appris pendant la simulation à la réalité (cela ne pose en général pas de problème pour les jeux, mais est moins évident pour les applications agissant sur le monde physique : les capteurs physiques ne correspondent pas tout à fait aux "perceptions" de nos fonctions, les actionneurs ne font pas toujours ce que l'on demande, les roues patinent, l'arrêt n'est pas instantané, …).
- Restriction 2
- Afin d'obtenir un apprentissage concluant, le nombre de simulations à réaliser est souvent très important. Pour se donner une idée, la 'difficulté de l'apprentissage' est souvent proportionnelle au nombre d'états de perception possibles. Ainsi, si la perception se limite à la couleur d'un feu de signalisation, il y a 3 états, si on doit 'attraper' cette couleur sur une grille de , ce qui fait états. Des méthodes existent afin de limiter l'effet de l'explosion du nombre d'états existent, mais elles ne seront pas abordées dans ce document (mélange de Q-learning et de réseaux de neurones en particulier).
4.1.2 Exemples pour se mettre dans le bain
Dans les exemples qui suivent, un agent reçoit des stimulus (perceptions), agit, et reçoit une récompense. Vous disposez des traces de ce qui s'est produit dans le passé. Votre but est de déterminer des règles de la forme "si perception alors action" dans le but de permettre à cet agent de maximiser les récompenses futures. Vous n'avez pour l'instant pas de connaissance sur le sujet, vous n'avez que votre bagage général pour obtenir vos premiers algorithmes.

- exemple 1
Deux perceptions possibles, 3 actions.
perception action récompense A 1 42 B 2 -4 B 3 -2 A 1 24 A 2 36 A 1 20 B 3 2 A 3 12 A 2 21 A 1 35 Résultat (à compléter) :
SI perception ALORS action A ? B ? Quelles nouvelles expériences seraient les plus intéressantes à demander à l'agent de réaliser ?
- exemple 2
L'agent va cette fois exécuter consécutivement deux actions, il y a 4 perceptions possibles et 2 actions disponibles.
- l'agent perçoit 'perception 1',
- il agit avec 'action 1',
- suite à cette action il arrive dans un nouvel état et reçoit un récompense 'récompense 1'
- il perçoit ce nouvel état par 'perception 2',
- il agit avec 'action 2',
- suite à cet action il obtient la récompense 'récompense 2'.
les perceptions possibles sont A, B, C, D les actions disponibles 1, 2.
perception 1 action 1 récompense 1 perception 2 action 2 récompense 2 A 1 1 C 1 4 A 1 1 C 2 3 A 1 -1 D 1 3 A 2 0 D 2 5 A 2 -2 D 1 2 A 2 -1 D 2 4 B 1 -1 D 1 3 B 2 0 D 2 4 B 1 2 A 1 1 B 2 3 B 2 -2 Résultat (à compléter) :
SI perception ALORS action A ? B ? C ? D ?
4.2 Préliminaire mathématique

Figure 7 : Calculs
Ce document a une approche pratique de l'apprentissage par renforcement. Cependant, il existe quelques points qui peuvent être mieux compris avec une approche mathématique (en particulier 4.2.2).
4.2.1 Suites décroissantes de limite nulle
Dans la plupart des algorithmes, il existe des paramètres qui doivent décroitre vers 0 au fil de l'exécution du programme.
Plusieurs types de suites, de décroissances plus ou moins lentes et de limite nulle sont classiquement utilisées, dont :
Pour limiter la vitesse de décroissance de la suite géométrique (même avec une raison de l'ordre de 0.99), on l'utilise souvent conjointement avec des paliers : la mise à jour de la valeur de n'est pas réalisée à chaque itération, mais uniquement toutes les 100 itérations (ou 200, ou 1000… [ce qui malheureusement va encore ajouter un paramètre à gérer]).
La décroissance logarithmique est lente, mais c'est celle qui est la plus proche de la théorie (les preuves de convergence des algorithmes sont souvent sous l'hypothèse d'une décroissance logarithmique) et a (un peu) plus de chances d'aboutir à un résultat correct (mais parfois au prix d'un temps de calcul plus long).
4.2.2 La formule de mise à jour
La plupart des algorithmes utilisent la même forme de formule de mise à jour. Cette formule, avec ses variations est , que l'on peut réécrire sous la forme d'une suite : . On s'intéresse à l'évolution de la distance entre et . On a :
On désire étendre le résultat précédent au cas où n'est plus une constante mais une suite de réalisations d'une variable aléatoire. Pour étudier cette modification, on définit :
- la suite de variables aléatoires , identiquement distribuées en fonction de et admettant une même espérance ,
- la suite de variables aléatoires par ,
- la suite des espérances des variables par .
On s'intéresse à l'évolution de la distance entre et . On a
- Attention
- Il y a convergence de l'espérance, il n'y a pas convergence de la variable, et il n'y a d'ailleurs pas de raison que la variable converge (chaque nouvelle réalisation de réalise une modification dont l'amplitude ne tend pas vers 0)! Pour obtenir de façon pratique (et artificielle) cette convergence, on choisit de prendre un petit (il n'y a toujours pas de convergence, mais les fluctuations sont alors de faible amplitude), et/ou de faire doucement tendre vers 0 au fil de l'algorithme [Il y a alors convergence en valeur, mais plus tend rapidement vers 0, moins la convergence en espérance est garantie. Il faudra choisir comment tendre vers O, ce qui complexifie le paramétrage de l’algorithme]). Il ne faut toutefois pas oublier que la vitesse de convergence de l'espérance dépend également de , plus est proche de 1, plus la convergence est rapide [car est plus proche de 0]. Un compromis est donc absolument nécessaire afin d'obtenir au mieux ces deux convergences !
- En conclusion
- En utilisant la formule proposée, on peut approcher petit à petit la valeur de l'espérance d'une
variable aléatoire en coagulant les valeurs des réalisations de cette variable. Cette méthode possède le très
regrettable inconvénient de nécessiter un réglage de paramètre , qui peut être laborieux et assez dépendant
du problème, mais profite des avantages suivants :
- la seule information stockée est l'estimation en cours (cela simplifie un peu les algorithmes),
- il y a une adaptation naturelle à des variations de la distribution de la variable aléatoire au fil des itérations ( n'est plus identiquement distribuée, mais peut évoluer lentement), les valeurs les plus récentes étant les plus importantes dans le calcul de l'estimation (on peut diminuer cet effet en choisissant que , la vitesse de décroissance permettant d'ajuster le poids du passé).
4.3 Apprentissage par renforcement

L'apprentissage par renforcement est une forme d'apprentissage non supervisé, qui a pour principe d'explorer le monde et de favoriser dans le futur la reproduction des situations qui dans le passé ont été valorisantes ou qui ont mené à des situations valorisantes.
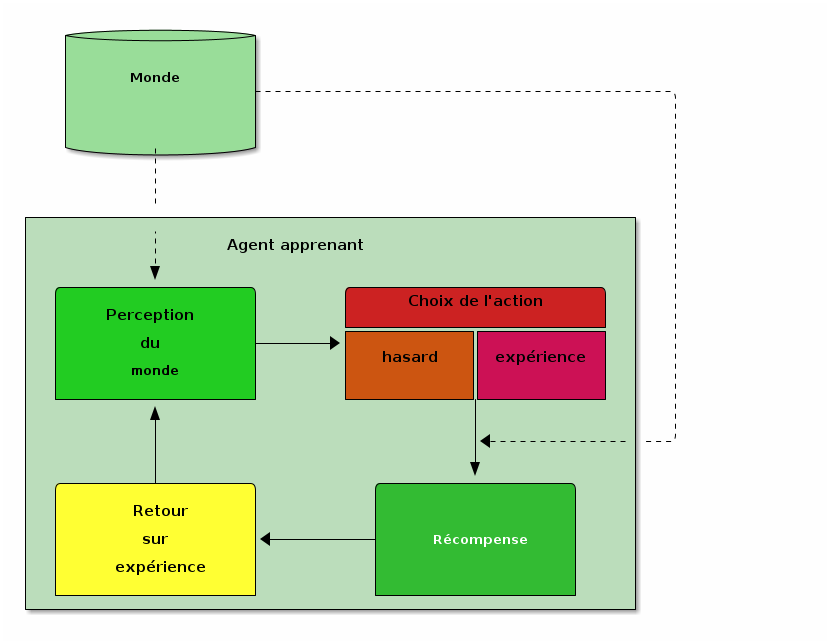
Le mécanisme peut être décrit par le cycle suivant :
- percevoir le monde,
- choisir une action parmi celles disponibles. Le choix de cette action prend en compte deux facteurs :
- découvrir et explorer, généralement simulé par un choix aléatoire (plus ou moins uniforme) parmi les actions possibles,
- profiter de son expérience, en choisissant préférentiellement des actions qui ont mené par le passé à des récompenses positives,
- percevoir une récompense suite à cette action (cette récompense peut être favorable -récompense positive- ou défavorable -récompense négative-),
- de temps en temps, faire un retour sur expérience afin d'améliorer la capacité à choisir une 'bonne' action dans le futur.
Il existe de nombreux algorithmes afin de mettre en œuvre l'idée de l’apprentissage par renforcement. Ce document vous en présente quelques uns, vous trouverez dans la bibliographie l'ouvrage de référence détaillant les algorithmes, leurs zones d'application, les comparant, et les justifiant par des preuves de convergence.
4.4 Qualité d'une action ou d'un état
Les méthodes introduites ici vont s'intéresser à deux façons de définir la qualité :
- une estimation de la qualité des états :
- une estimation de la qualité des actions dans un état :
Ces façons de mesurer la qualité modifieront les algorithmes, en conservant les mêmes idées de ce qui doit être fait.
4.4.1 Présentation de v(s)
La fonction associe à un état du système sa qualité. Ainsi, un agent rationnel choisira préférentiellement de se rendre dans un état de qualité élevée plutôt que dans un état de faible qualité. La valeur de ne représente pas uniquement le bénéfice immédiat (récompense obtenue parce qu'on atteint cet état), mais également le bénéfice que l'on peut espérer obtenir à plus long terme si on transite par cet état.
Une fois les qualités de tous les états connus, leur utilisation peut suivre la boucle suivante :
- percevoir la situation ( = connaitre ),
- pour chaque action disponible, générer l'état qui serait (au conditionnel !!!) atteint,
- choisir parmi les actions possibles préférentiellement celle qui mène à un état de qualité maximale. Le problème de cette façon de juger de la qualité par la qualité des états vient d'apparaitre : il est nécessaire de pouvoir générer les états sans pour autant effectuer réellement les actions qui permettraient de les atteindre.
4.4.2 Présentation Q(s,a)
La fonction associe à une perception de l'agent la qualité de chacune des actions disponibles dans cet état. L'état du système est défini par les perceptions de l'agent. La fonction prend deux arguments, (ou , puisque l'état n'est connu que via les perceptions) et et renvoie la valeur de la qualité de l'action lorsque la perception du monde est . On peut imaginer d'implémenter par un tableau 2D, dont les indexes des lignes représentent les différentes perceptions possibles et les indexes des colonnes les différentes actions possibles. La valeur située en ligne et colonne indique la qualité de l'action lorsque la perception du monde est .
Par exemple : un véhicule se trouve devant un feu tricolore. Sa perception de l'environnement se limite à la couleur du feu, et ses actions possibles sont : s'arrêter, rouler. On peut alors imaginer la table des qualités qui suit :
| s'arrêter | rouler | |
|---|---|---|
| couleur feu = vert | -1 | 5 |
| couleur feu = orange | 4 | -1 |
| couleur feu = rouge | 10 | -10 |
On augmentant les perceptions (ici, en tenant compte de la vitesse actuelle du véhicule), on peut améliorer la modélisation du monde (on est encore loin d'un modèle pertinent à implémenter dans un véhicule autonome…) :
| s'arrêter | rouler | |
|---|---|---|
| couleur feu = vert, vitesse actuelle = lente | -1 | 8 |
| couleur feu = vert, vitesse actuelle = rapide | -2 | 9 |
| couleur feu = orange, vitesse actuelle = lente | 4 | -2 |
| couleur feu = orange, vitesse actuelle = rapide | 3 | 0 |
| couleur feu = rouge, vitesse actuelle = lente | 10 | -10 |
| couleur feu = rouge, vitesse actuelle = rapide | 10 | -9 |
Une fois cette table d'association créée, son utilisation peut suivre la boucle suivante :
- percevoir la situation,
- choisir parmi les actions possibles préférentiellement celle avec la qualité la plus élevée.
4.4.3 Valeurs attendues
On s'intéresse dans ce paragraphe aux valeur que l'on voudrait trouver dans la table, pas à comment les fabriquer.
Suite à une observation, la qualité d'une action est la qualité de l'état atteint lorsque l'on effectue cette action. Afin de définir la qualité d'un état, voici les points qu'il faut considérer :
- La qualité n'est pas toujours une mesure immédiate : avant de savoir si le résultat d'une action est bon, il est souvent nécessaire de la juger à l'aune de ses conséquences. Dévaliser une banque peut procurer une récompense immédiate, qui après quelques temps peut ne pas être suffisante pour compenser les désagréments que cette action engendre. La qualité est un mélange entre les récompenses obtenues à court terme et les récompenses futures issues de cet état. Suivant l'adage "un tien valant mieux que deux tu l'auras !", on va généralement pondérer dans le calcul de la qualité plus fortement le futur proche que le futur lointain.
- La qualité d'un état n'est pas toujours la même, même si la situation perçue est la même. Par exemple : griller un feu rouge ne provoque pas toujours la mort. L'état du monde définit les perceptions mais les perceptions ne définissent pas l'état du monde, il peut y avoir plusieurs états du monde qui créent la même perception. La qualité est un mélange entre les différentes qualités des états qui peuvent être atteints.
La qualité d'une action dans une certaine situation peut donc être définie comme une moyenne pondérée des espérance des qualité des états qui en découlent.
Dans la première table des qualités dans l'exemple des feux de signalisation, la valeur de 5 (feu vert, rouler) correspond à un mélange entre les accidents (plus ou moins graves) possibles (même si le véhicule est passé au vert), au plaisir d'être rentré plus tôt, au plaisir de la rencontre imprévue un peu plus tard, … On ne sait pas a priori ce que cette valeur présage, elle indique uniquement que c'est une état qui dans le passé nous aurait permis d'espérer une qualité de 5.
La qualité d'un état terminal est la récompense obtenue dans cet état (trésor trouvé, mort, …). La qualité d'un état non terminal dépend des actions qui seront réalisées depuis cet état. On va se placer dans la situation où le prochain choix sera rationnel (le meilleur possible d'après les connaissances du moment) : la qualité d'un état est la qualité du meilleur état que l'on peut atteindre après une action.
La qualité d'un état est l'espérance des récompenses que l'on peut atteindre depuis l'état pour les dates de temps futures : , pondérées par un facteur
- version se focalisant sur les états
En supposant que les tous les états ont leur qualité calculée comme précédemment, cette équation devient:
NB : le maximum de la formule a pour origine que le choix de l'action qui sera réalisée est rationnel : pendant l'exploitation, on choisit l'action qui possède la plus haute qualité. Dans l'éventualité où l'exploitation ferait un choix notablement différent, il pourrait être approprié de modifier ce de façon à ce qu'il corresponde à la politique d'utilisation choisie. [Les deux façons de choisir une action présentées dans la suite sont compatibles avec le utilisé ici.]
- version se focalisant sur les actions
La qualité d'une action réalisée dans l'état , en notant les états résultants de après l'action est
NB : voir ci-dessus dans la version 'états'.
4.5 Choix d'une action
Parfois, les choses sont simples, et on choisit l'action de qualité maximale, parfois les perceptions sont insuffisantes pour caractériser l'environnement, ou la table est encore imparfaite, et il vaut mieux ne pas se fier totalement aux qualités qui y sont indiquées. On préfère introduire une variabilité dans le choix de l'action à réaliser. Deux méthodes sont principalement utilisées afin d'atteindre cet objectif : 'ε-greedy' et 'preference learning base'.
4.5.1 Choix de l'action : ε-greedy
du temps, on choisit l'action de qualité maximale, et on tire en aléatoire uniforme l'action à exécuter parmi toutes celles possibles. Cela permet de modéliser deux comportements :
- l'exploration
- On ne se préoccupe pas de ce qui a déjà été appris. Cette partie exploratoire est prépondérante lorsque les connaissances sont faibles et diminue au fil de l'apprentissage, de façon à ne pas toujours perdre du temps à explorer des situations non pertinentes. Comme on ne tient pas du tout compte de ce qui a déjà été appris, il est possible de faire émerger des comportements totalement nouveaux.
- l'exploitation
- Une fois le modèle appris, la partie exploratoire est terminée, on utilise l'information emmagasinée
en choisissant à chaque itération l'action de qualité maximale. Dans une situation où l'environnement n'est pas
stable, la phase exploratoire ne disparait pas totalement, ce qui permet au programme de :
- par défaut préférer ce qui a fonctionné par le passé,
- sans supprimer la possibilité d'une innovation.
4.5.2 Choix d'une action : 'preference learning-base'
Les valeurs dans la table ne sont plus interprétées comme des qualités mais comme des préférences (et même si on préfère le chocolat au bonbons, il n'est pas impossible de temps en temps de choisir les bonbons plutôt que le chocolat, alors que pour la qualité, on choisit toujours la meilleure possible). Pour implémenter cette idée, on va utiliser la table des qualités afin de définir une loi de distribution de probabilités, qui rende plus probables les actions de qualités les plus fortes, sans pour autant supprimer la possibilités des autres. On peut utiliser la distribution de Boltzmann (ou distribution de Gibbs, selon la littérature) afin de choisir cet état.
Entrées :
- s la situation
- Q la méthode permettant de connaitre la qualité d'une action dans une situation donnée
- T la 'température', c'est un réel strictement positif
Sortie :
- une action tirée selon la distribution de Gibbs
Processus :
- Définir L : la liste des actions possibles depuis l'état s
- Définir N le nombre d'éléments de L
- Pour chaque action a de L:
- Définir E(a) : l'énergie de a est E(a) = exp(Q(s,a)/T)
- Définir Z : la somme des énergies des éléments de L
- Définir action = L[N-1], c'est l'indice de l'action par défaut
- Définir alpha : un réel tiré en aléatoire uniforme dans [0 ; 1[
- Définir cumul = 0
- pour a dans L :
- cumul += E(a)/Z
- si alpha <= cumul :
- action = a
- break
- renvoyer action
Pour comprendre le fonctionnement de cet algorithme, on commence par oublier le paramètre . Le passage par l'exponentielle rend les énergies strictement positives. La normalisation par Z rend , ce qui rend ces quantités conformes à des mesures de probabilités. Ainsi, les permettent de définir une distribution de probabilité que l'on utilise comme une loi tabulés (Cf. compléments algorithmiques) Le critère de "plus la qualité est élevée, plus la probabilité de réaliser l'action" est respecté (stricte croissance de l'exponentielle).
Le paramètre de température a l'effet suivant : lorsque la température est élevée, comme l'exponentielle est 'constante' au voisinage de 0, les valeurs de sont toutes les mêmes, et la distribution tend vers une distribution uniforme ; on retrouve la partie exploration de la version ε-greedy. Lorsque la température est proche de 0, les écarts entre les sont amplifiés, et à l’extrême, la distribution se limite alors aux actions dont la qualité est maximale ; on retrouve la partie 'choix de la qualité maximale' de ε-greedy (piste pour s'en convaincre : on met en facteur dans la quantité qui correspond à la qualité maximale, et on obtient alors , où est le nombre d'états possédant la même qualité maximale ; après la normalisation, il ne reste donc plus que les états de qualité maximale).
4.6 Apprentissage des qualités
4.6.1 Présentation, notations
Au départ l'agent ne dispose d'aucune information sur la qualité des actions qu'il peut effectuer. On peut donc au choix initialiser les qualités à 0 (ou à une valeur approxiamative de l'espérance des récompenses si les récompenses ne sont pas centrées sur 0), ou à des valeurs aléatoires tirées en uniforme dans un domaine similaire à celui dans lequel les récompenses sont définies (on n'initialise pas entre -100 et 100 sir les récompenses sont entre -1 et 2, on choisit un domaine similaire).
L'agent est placé dans un état initial , il choisit son action en utilisant pour cela sa connaissance actuelle des qualités, il atteint alors l'état , … et ainsi de suite jusqu'à :
- atteindre un état terminal (fin de partie : la tâche a plus ou moins bien été accomplie)
- dépasser un nombre d'état jugé comme plus que suffisant (cela permettra d'éviter des boucles infinies)
Il résulte de cet enchaînement d'actions (que l'on appelle une époque, ou un 'run') les suites suivantes :
- la suite des états parcourus ,
- la suite des actions réalisées [ Attention important : désigne l'action réalisée au départ de l'état ]
- la suite des récompenses obtenue [ Attention important : désigne la récompense obtenue en atteignant l'état c'est à dire après l'action ]

4.6.2 Mise à jour
Les formules de mises à jour ont été créées en fusionnant les formules qui définissent les qualités (qualité d'un état ou d'une action) avec le préliminaire mathématique qui permet d'estimer de façon itérative une espérance.
- modification immédiate
L'agent choisit une action, l'exécute, et met à jour la qualité correspondante en fonction des récompenses obtenues. Les listes présentées (les suites , et ) sont limitées à leur premier terme (). Comme la mise à jour est immédiate, si les récompenses sont principalement à long terme, l'apprentissage risque d'être extrêmement long : pour modifier (ou ), il faut arriver sur un état qui a déjà été modifié, donc si au départ l'agent est dans un état assez lointain d'une récompense, il ne va rien apprendre, et tout nouvel apprentissage ne sera pleinement utilisé que dans un futur lointain, le temps qu'il influence les autres qualités pouvant être assez long. Quoi que cette méthode soit la plus simple à implémenter, elle n'est en général pas la plus efficace et elle ne sera pas développée dans la suite de ce document.
- modification après un 'run'
On fait la mise à jour après avoir obtenu : soit un nombre de récompenses significatif (positives comme négatives), ou après avoir atteint un état terminal [dans le cas où le run s'est terminé par dépassement du nombre d'actions, on choisira ou non de faire la mise à jour, ou de la faire avec un coefficient plus petit, mais l'information à tirer de cette époque est faible]. Cette méthode est en général préférable à la précédente car il va être possible de maximiser l'utilisation de l'information obtenue dans un apprentissage aux autres apprentissages de la même époque en procédant par rétro-propagation : on effectue les mises à jour en partant de l'état car c'est celui qui contient le plus d'information, puis on remonte vers l'état . Ainsi, lorsque l'on met à jour une qualité, on utilise le résultat des mises à jour des qualités qui viennent d'être faites.
- Le synopsis du processus d'apprentissage est
- Initialiser les qualités, les paramètres d'apprentissage,
- Générer une instance du monde,
- Réaliser un 'run', c'est à dire une suite d'actions menant si possible à un état terminal,
- A partir des résultats du 'run', modifier les qualités par rétro-propagation,
- Modifier si nécessaires les paramètres d'apprentissage,
- Retour en 1 jusqu'à (condition à choisir de façon adéquate).
4.6.3 cas : qualité des états
La difficulté d'utilisation de cette formule provient du calcul du maximum qui se fait sur l'ensemble des situations accessibles. Il est en général assez aisé d'énumérer les actions possibles à un instant donné, mais pour connaître les états qui en résultent… il est nécessaire d'effectuer les actions. Ainsi, on va construire pour chaque état la liste des situations qui lui sont directement accessibles. Par conséquent, afin que cette stratégie soit possible, il faudra être capable de mémoriser un état du monde afin de pouvoir y revenir par la suite [attention, ici il y a une nuance : il ne suffit pas de pouvoir sauvegarder un état (qui ne correspond qu'à une perception du monde), il est nécessaire de pouvoir sauvegarder l'état du monde afin de pouvoir reprendre la simulation là où elle en était].
Ce retour sur une situation sauvegardée n'est possible que si on a accès à tous les paramètres qui caractérisent le monde, ce qui n'est en général pas le cas si l'apprentissage se déroule dans le monde réel.
L'algorithme va consister à créer pour chaque état la liste des états auxquels il permet d'accéder en une action. Pour cela, on modifie l'algorithme de la suite des déplacements : avant de se déplacer depuis un état , pour chacune des actions possibles, on vérifie que l'état qui serait atteint est bien dans la liste des états directement accessibles depuis , et s'il ne l'est pas on l'ajoute à cette liste. On dispose alors d'un graphe orienté des perceptions .
- algorithme dans le cas d'un apprentissage après une suite d'actions concluante
Entrées :
- s0, s1, ... sn la suites des états
- r0, r1, ..., r(n-1) la suite des récompenses
- G table des fils des perceptions, G[x] est l'ensemble des états accessibles depuis l'état x
- v la méthode permettant de connaitre la qualité d'un état
Sortie :
- v mise à jour
Processus :
- V(sn) += epsilon * (rn - v(sn))
- pour i = n-1 à 0 par pas de -1
- Définir M le maximum des v(s') pour s' dans G[si]
- v(si) += epsilon * (ri + gamma * M - v(si))
4.6.4 cas : qualité des actions
En notant l'état atteint après avoir effectué l'action en l'état :
Cette méthode n'a pas le problème de la sauvegarde de l'état du monde de la méthode précédente, mais possède le désavantage de posséder plus de valeurs de qualités à estimer que la précédente". Dans la méthode précédente, on devait estimer une qualité par état, alors que dans cette méthode, il faut estimer la qualité de chaque action effectuée dans chaque état, ce qui signifie que le nombre de qualités à estimer est multiplié par le nombre d'actions possibles. Par conséquent, il y a un risque que cette méthode nécessite plus de temps pour obtenir un résultat concluant.
- algorithme dans le cas d'un apprentissage après une suite d'actions concluante
Entrées :
- s0, s1, ... sn la suites des états
- a0, a1, ..., a(n-1) la suite des actions réalisées
- r0, r1, ..., r(n-1) la suite des récompenses
- Q la méthode permettant de connaitre la qualité d'une action dans un état
Sortie :
- Q mise à jour
Processus :
- Q( s(n-1), a(n-1) ) += epsilon * (rn - Q( s(n-1),a(n-1) ))
- pour i = n-2 à 0 par pas de -1
- Définir M le maximum des Q(s(i+1), a) pour toute action a possible
- Q(si, ai) += epsilon * (r(i+1) + gamma * M - Q(si,ai) )
4.6.5 Double Q-learning
- Problématique
La méthode d'apprentissage de la table possède un biais important bien étudié en statistiques lié à la fonction max qui tend à surestimer les quantités.
Une façon de supprimer ce biais est d'utiliser deux fonctions indépendantes, la première sert dans la phase de choix de l'action à effectuer, la seconde est la fonction que l'on veut apprendre. Le problème est qu'on ne dispose pas (avant que l'apprentissage ne soit terminé) de la fonction qui sert à faire le choix de l'action (c'est celle que l'on veut créer).
Existe-t-il une solution ? oui ! On va créer en simultané les deux fonctions, en conservant leur indépendance. On initialise deux fonctions et .
- Pendant la phase d’apprentissage (après un run), à chaque itération, on choisit aléatoirement laquelle sera l'estimateur du choix de l'action à réaliser (et donc l'autre sera la fonction que l'on apprend). Les deux fonctions suivent statistiquement la même distribution mais correspondent à des variables indépendantes puisqu'elles ont appris sur des exemples différents !
- Pendant le run, afin de ne pas gaspiller d'information par rapport à ce qui a été appris, on utilise pour faire les choix d'action non pas (ou de façon équivalente ) mais .
Cette variation de l'algorithme du -learning n'est pas particulièrement difficile à mettre en œuvre, et peut apporter une grande amélioration par rapport à l'algorithme de base, aussi bien pour la vitesse de convergence que pour les résultats finaux (même en laissant l'algorithme normal fonctionner aussi longtemps qu'on le désire, le biais ne disparaît pas).
- Algorithme
- run
il n'y a pas de modification du code du run (que l'on choisisse 'ε-greedy' ou 'preference learning rate'), mise à part la fonction de qualité qui est maintenant
- apprentissage
L'algorithme qui suit est à appliquer après chaque run.
Entrées : - s0, s1, ... sn la suites des états - a0, a1, ..., a(n-1) la suite des actions réalisées - r0, r1, ..., r(n-1) la suite des récompenses - Q1 une méthode permettant de connaitre la qualité d'une action dans un état - Q2 une méthode permettant de connaitre la qualité d'une action dans un état Sortie : - Q1 et Q2 mis à jour Processus : - Définir alpha, réel aléatoire tiré en uniforme dans [0 ; 1[ - Si alpha <0.5 - Définir Q_apprentissage = Q1 et Q_estimation = Q2 - Sinon - Définir Q_apprentissage = Q2 et Q_estimation = Q1 - Q_apprentissage(s(n-1), a(n-1)) += epsilon * (r(n) - Q_apprentissage(s(n-1),a(n-1)) ) - pour i = n-2 à 0 par pas de -1 - Définir alpha, réel aléatoire tiré en uniforme dans [0 ; 1[ - Si alpha <0.5 - Définir Q_apprentissage = Q1 et Q_estimation = Q2 - Sinon - Définir Q_apprentissage = Q2 et Q_estimation = Q1 - Définir A l'action qui maximise Q_learn(s(i+1), a) pour toute action a possible - Q_apprentissage(si, ai) += epsilon * (r(i+1) + gamma * Q_estimation(s(i+1), A) - Q_apprentissage(si,ai) )
- run
4.6.6 SARSA
- Problématique
Les états que l'on utilise dans les algorithmes correspondent à des perceptions du monde. Le problème est qu'il n'y a pas toujours de bijection entre les états du monde et les états . Par exemple, imaginons un agent dans un labyrinthe, ses perceptions sont limitées à la position des murs (ou absence de murs) sur le carré qu'il occupe. On peut imaginer qu'un trésor se trouve au nord d'une salle ayant un mur à l'est et un mur à l'ouest et qu'il existe un piège au nord d'une autre salle ayant également un mur à l'est et un mur à ouest. L'état (est, ouest) peut mener aussi bien à une récompense positive qu'à une récompense négative. Prendre le maximum entre les deux récompenses signifie qu'on ira toujours au nord, comme si c'était l'agent qui décidait ce qu'il y a dans la salle au nord. Peut-être est-il intéressant d'aller au nord car les pièges à cet endroit sont rares et peu pénalisants, peut-être vaut-il mieux chercher un autre chemin ; en tous cas, prendre automatiquement la meilleure des récompenses possibles ne semble pas optimal.
- Algorithme dans le cas Q(s,a)
- run
Inchangé.
- Apprentissage
Entrées : - s0, s1, ... sn la suites des états - a0, a1, ..., a(n-1) la suite des actions réalisées - r0, r1, ..., r(n-1) la suite des récompenses - Q une méthode permettant de connaitre la qualité d'une action dans un état Sortie : - Q mis à jour Processus : - Q_apprentissage(s(n-1), a(n-1)) += epsilon * (r(n) - Q_apprentissage(s(n-1),a(n-1)) ) - pour i = n-2 à 0 par pas de -1 - Q_apprentissage(si, ai) += epsilon * (r(i+1) + gamma * Q_apprentissage(s(i+1), a(i+1)) - Q_apprentissage(si,ai) )L'idée de l'algorithme SARSA (state action reward state action) est de réaliser un run comme précédemment, mais pendant la phase d'apprentissage, remplacer le maximum par la valeur de la qualité de l'action qui a effectivement été réalisée.
- Avantages
- l'algorithme est plus simple à coder, chaque phase d'apprentissage est rapide,
- les valeurs trouvées tiennent compte, non pas du meilleur cas, mais des cas effectievement rencontrés, et effectue un calcul d'espérance sur les situations atteignables (c'était le but recherché),
- comparé à l'algorithme du Q-learning, les solutions trouvées sont plus robustes (l'exemple donné par Sutton est : si on cherche un chemin, le Q-learning n'hésitera pas longer des falaises si cela donne le chemin le plus court, alors que SARSA privilégiera des chemins évitant les plus gros dangers).
- Inconvénients
- la contrepartie de sa robustesse est qu'il ne trouve en général pas les meilleurs solutions,
- il est souvent plus lent que le Q-learning.
- run
4.6.7 SARSA avec 'double learning'
Le problème lié au maximum reste n'est pas présent dans la phase d’apprentissage de SARSA, mais existe toujours au moment du run, lors du choix de l'action à réaliser. L'influence de cette modification sera donc plus faible que dans le 'double Q-learning' mais peut tout de même améliorer les résultats.
Pour y palier, on peut encore une fois utiliser deux fonctions de qualité, afin de séparer l'estimateur sur lequel on a choisi l'action de celui que l'on apprend.
Entrées :
- s0, s1, ... sn la suites des états
- a0, a1, ..., a(n-1) la suite des actions réalisées
- r0, r1, ..., r(n-1) la suite des récompenses
- Q1, Q2 les fonctions défiissant la qualité d'une action dans un état
Sortie :
- Q1 et Q2 mis à jour
Processus :
- Définir alpha, réel aléatoire tiré en uniforme dans [0 ; 1[
- Si alpha <0.5
- Définir Q_apprentissage = Q1 et Q_estimation = Q2
- Sinon
- Définir Q_apprentissage = Q2 et Q_estimation = Q1
- Q_apprentissage(s(n-1), a(n-1)) += epsilon * (r(n) - Q_apprentissage(s(n-1),a(n-1)) )
- pour i = n-2 à 0 par pas de -1
- Q_apprentissage(si, ai) += epsilon * (r(i+1) + gamma * Q_estimation(s(i+1), a(i+1)) - Q_apprentissage(si,ai) )
4.7 Conseils pour le code
4.7.1 Paramètres
Comme vous allez vous en rendre compte, le réglage des paramètres peut être assez désagréable. Afin de pouvoir manipuler les algorithmes, les différents paramètrages sont conservés dans une structure découpée si nécessaire en unions (lorsque des paramètres son incompatibles) et structures (s'ils sont compatibles entre eux). Il est conseillé que tout soit stocké dans le même .c (ou dans un même fichier texte de configuration si vous voulez quelque chose de plus ergonomique pour faire les tests). Les paramètres Elle contient :
- paramètres de définition du monde
- paramètres de dimensionnement
- paramètres définissant les récompenses
- paramètres d'initialisation
- paramètres de l'apprentissage
- pointeurs sur les fonctions choisies : ce n'est pas obligatoire, mais cela peut rendre les modifications de code plus agréables, vous pouvez avoir différentes fonctions (par exemple learn_state, learn_Q , learn_Q_double, learn_sarsa, …) et la fonction à utiliser pendant cet apprentissage est précisée dans le fichier de config par un pointeur sur fonction… à vous de voir si cela ne vous effraie pas.
- nombre d'époques
- nombre maximum d'états dans une époque
- ξ, comment ξ décroît
- α, comment α décroît
- γ, comment γ décroît
- paramètres sur les états
- paramètres pour définir les états
- paramètres pour définir les actions
- paramètres pour l'initialisation
- paramètres de l'exploration
- pour ε -greedy : valeur de départ, comment ε décroît,
- pour 'preference learning base' : valeur initiale de la température, comment décroît,
Il est de plus conseillé que toutes les fonctions prennent en entrée un pointeur sur cette structure : cela ne coûte pas cher et cela simplifie l'utilisation des fonctions (on ne se pose pas de question, c'est le premier paramètre à l'appel de toutes les fonctions).
Même si vous ne travaillez pas avec un fichier de configuration, il est intéressant d'avoir une fonction qui à chaque test sauvegarde les paramètres, auxquels sont ajoutés la date et l'heure (et si possible les résultats de l'apprentissage, mais vous verrez que dans la pratique ce point est plus difficile). Cela permet de vérifier ce qui a été testé. Conserver une trace des tests réalisés et très important afin de ne pas refaire 100 fois les mêmes choses, et oublier toujours les mêmes.
4.7.2 Principales fonctions
Voici une liste de quelques fonctions qui peuvent vous aider à commencer à structurer votre code. N'oubliez pas que toutes ces fonctions ont également en entrée un accès à tous les paramètres.
- fonction de perception : prend l'état du monde en entrée et renvoie l'état de perception (),
- fonction d'évolution : prend en entrée le monde et une action et modifie l'état du monde,
- fonction de récompense : prend le monde en entrée et renvoie la récompense associée à cet état du monde,
- fonction d'énumération des actions : prend le monde en entrée et renvoie une énumération des actions possibles,
- fonction de choix d'une action : prend en entrée une perception, le monde et renvoie l'action choisie.
- fonction principale :
- Initialiser les paramètres, les sauvegarder
- Si c'est un apprentissage de qualité d'états : initialiser dans la table des successeurs des états
- Pour époque = 0 à nb_époques-1
- Créer le monde
- Pour pas = 0 à nb_max_actions_dans_epoque-1
- Récupérer la récompense sur le monde actuel, la stocker
- Percevoir l'état, le stocker
- Si c'est un apprentissage de qualité d'états : mettre à jour les successeurs de l'état perçu
- Choisir l'action à réaliser, la stocker
- Appliquer l'action choisie au monde
- Si l'état atteint est terminal : break
- Percevoir le monde, le stocker
- Récupérer la récompense sur le monde actuel, la stocker
- Réaliser une phase d'apprentissage à partir des informations conservées
- Modifier si nécessaire les paramètres
- Sauvegarder dans un fichier des qualités
- Afficher un score (ou autre) montrant à quel point l'apprentissage a été concluant
4.8 Bibliographie
Une unique référence pour bien démarrer : Reinforcement learning : Sutton & Barto.
5 Compléments algorithmiques
5.1 Tirer une v.a. selon une loi tabulée
Lorsque la distribution de probabilité d'une variable aléatoire est connue sous la forme d'un tableau, on peut générer des réalisations de cette variable par l'algorithme qui suit.
Entrée :
- T un tableau de n cases, dont la case i contient P(X=i)
Sortie :
- un entier i qui est une réalisation de X
Processus :
- Définir alpha : un réel tiré en aléatoire uniforme dans [0 ; 1[
- Définir s = n-1 // par défaut, le programme renvoie la dernière réalisation possible
- Définir cumul = 0 // on construit les probabilités cumulées
- Pour i = 0 à à n-2 :
- cumul += T[i]
- Si alpha < cumul :
- s = i
- break
- renvoyer s
5.2 Mélanger le éléments d'un tableau
L'algorithme classique afin de mélanger les éléments d'un tableau est l'algorithme de Fisher-Yates. Il est simple à implémenter et efficace. Sa complexité est où est la taille du tableau et la complexité de la génération d'un nombre aléatoire de la taille d'une case du tableau.
Entrée :
- T un tableau de taille N
Sortie :
- T a été modifié, il contient une permutation de ses éléments, tirée en aléatoire uniforme
Process :
- Pour i = n-1 à 1 par pas de -1
- Définir j : un entier tiré en aléatoire uniforme dans [0 .. i]
- echanger le contenu des cases i et j de T
5.3 Bibliographie
Pour ceux qui ont besoin de précision sur une structure de données, ou un algorithme de parcours, recherche, … le premier endroit où chercher :

Figure 11 : Avant d'aller chercher ailleurs !
6 Généralités sur le code
- Ce n'est pas après 3 jours que l'on écrit son premier makefile, c'est le plus vite possible :
- developpez.net
- et pour ceux qui ont beaucoup de difficultés avec les makefiles, voici une base possible :
SRC=q_learning.c parameters.c general.c SRC+=world.c etc1.c etc2.c #SRC=$(wildcard *.c) # en commentaire, je ne suis pas un grand amateur EXE=q_learning.out CC=gcc CFLAGS:=-Wall -Wextra -MMD -0g -g $(sdl2-config --cflags) #CFLAGS:=-Wall -Wextra -MMD -O2 $(sdl2-config --cflags) # pour la version release LDFLAGS:=-lSDL2_image -lSDL2_ttf -lSDL2_gfx -lm -lSDL2 OBJ=$(addprefix build/,$(SRC:.c=.o)) DEP=$(addprefix build/,$(SRC:.c=.d)) all: $(OBJ) $(CC) -o $(EXE) $^ $(LDFLAGS) build/%.o: %.c @mkdir -p build $(CC) $(CFLAGS) -o $@ -c $< clean: rm -rf build core *.o -include $(DEP)
7 Valgrind
Valgrind (avec son outil par défaut memcheck) analyse l'exécution d'un programme pour, entre autres, rapporter :
- la quantité de mémoire allouée dynamiquement,
- les fuites mémoires (avec numéro de ligne de l'allocation liée si compilé avec `-g`),
- les erreurs d'accès en lecture ou écriture à la mémoire,
- les erreurs d'utilisation en lecture d'un variable non initialisée.
- Valgrind ne remplace pas un débogueur, en particulier dans une situation d'échec d'exécution, comme lors d'une erreur de segmentation (segfault).
Pour des explications plus précises et complètes, voir le manuel de Valgrind.
7.1 Rapport sur l'utilisation mémoire
Une sortie possible de Valgrind :
==3719130== Memcheck, a memory error detector ==3719130== Copyright (C) 2002-2017, and GNU GPL'd, by Julian Seward et al. ==3719130== Using Valgrind-3.16.1 and LibVEX; rerun with -h for copyright info ==3719130== Command: ./a.out ==3719130== ==3719130== ==3719130== HEAP SUMMARY: ==3719130== in use at exit: 0 bytes in 0 blocks ==3719130== total heap usage: 3 allocs, 3 frees, 70 bytes allocated ==3719130== ==3719130== All heap blocks were freed -- no leaks are possible ==3719130== ==3719130== For lists of detected and suppressed errors, rerun with: -s ==3719130== ERROR SUMMARY: 0 errors from 0 contexts (suppressed: 0 from 0)
La section HEAD SUMMARY indique le nombre d'allocations, de libérations ainsi
que le total d'octets alloués.
Valgrind indique ensuite que All heap blocks were freed -- no leaks are
possible, il n'y a pas eu de fuite mémoire lors de cette exécution du programme.
Lorsqu'un programme ne libère pas toute sa mémoire, le rapport peut ressembler à ceci :
==3720916== HEAP SUMMARY: ==3720916== in use at exit: 10 bytes in 1 blocks ==3720916== total heap usage: 3 allocs, 2 frees, 70 bytes allocated ==3720916== ==3720916== LEAK SUMMARY: ==3720916== definitely lost: 10 bytes in 1 blocks ==3720916== indirectly lost: 0 bytes in 0 blocks ==3720916== possibly lost: 0 bytes in 0 blocks ==3720916== still reachable: 0 bytes in 0 blocks ==3720916== suppressed: 0 bytes in 0 blocks ==3720916== Rerun with --leak-check=full to see details of leaked memory
Valgrind indique ici qu'il n'y a eu que deux libérations, alors que 3 allocations avaient été réalisées.
La section suivante du rapport Valgring, LEAK SUMMARY, précise comment l'accès
à la mémoire a été perdu.
7.2 Rapport sur les variables non initialisées
Pour le code source suivant :
1: #include <stdio.h> 2: 3: void foo(int condition, int value) { 4: if(condition) printf("value: %d\n", value); 5: else puts("no display"); 6: } 7: 8: int main() { 9: int i, j = 0; 10: 11: foo(i, j); 12: }
Sans l'option -g à la compilation, le résultat obtenu est alors :
==3729129== Conditional jump or move depends on uninitialised value(s) ==3729129== at 0x109144: foo (in /tmp/tmp.1622971724.30Oq/a.out) ==3729129== by 0x109174: main (in /tmp/tmp.1622971724.30Oq/a.out)
Avec l'option -g :
==3729359== Conditional jump or move depends on uninitialised value(s) ==3729359== at 0x109144: foo (main.c:4) ==3729359== by 0x109174: main (main.c:13)
Dans la fonction foo, à la ligne 4, on utilise la variable condition en
lecture sans que celle-ci ait été préalablement affectée. Cette variable est un
paramètre de la fonction, il faut donc aller au lieu de l'appel. Valgrind nous
indique que la ligne 13 de la fonction main appelle foo avec les arguments
i et j. La variable i correspond à la condition dans la fonction
foo : il s'agit de la variable non initialisée (ce que l'on vérifie facilement
à la ligne 11).
7.3 Lecture/écriture invalide
Considérons le code source suivant :
1: #include <stdlib.h> 2: 3: int main() { 4: int n = 5; 5: int *tab = malloc(n*sizeof *tab); 6: for(int i = 0; i <= n; ++i) 7: tab[i] = i; 8: 9: free(tab); 10: }
Une analyse par valgrind, sans l'option -g à la compilation, fournit le rapport :
==3845342== Invalid write of size 4 ==3845342== at 0x109189: main (in /tmp/tmp.1622971724.30Oq/a.out) ==3845342== Address 0x4a3a054 is 0 bytes after a block of size 20 alloc'd ==3845342== at 0x483877F: malloc (vg_replace_malloc.c:307) ==3845342== by 0x109164: main (in /tmp/tmp.1622971724.30Oq/a.out)
Avec l'option -g à la compilation on obtient :
==3846517== Invalid write of size 4 ==3846517== at 0x109189: main (main.c:7) ==3846517== Address 0x4a3a054 is 0 bytes after a block of size 20 alloc'd ==3846517== at 0x483877F: malloc (vg_replace_malloc.c:307) ==3846517== by 0x109164: main (main.c:5)
Cela permet de détecter une erreur dite « off-by-one ». En effet, il y a une
écriture invalide de taille 4 (Invalid write of size 4) à la ligne 7 du
programme, en accédant à un espace mémoire alloué à la ligne 5 du programme.
Lorsque l'on connaît la machine sur laquelle on exécute le programme, on peut
savoir qu'un int y possède une taille de 4 octets (le standard oblige un
minimum de 2 octets). Il s'agit donc d'une affectation d'un entier hors des
limites allouées pour le tableau. On corrige la boucle qui va jusqu'à n
inclus pour s'arrêter avant : le test devient i < n.
7.4 Valgrind et la SDL
Lorsque le programme analysé par Valgrind utilise des bibliothèques, il peut arriver que le rapport comporte des éléments indésirables. CE sont des erreurs dont l'origine n'est pas notre programme, mais qui proviennent de la bibliothèque. Par exemple, utiliser la SDL, selon sa version, et les différents éléments du système peut ainsi faire apparaître des « fuites mémoire » qui ne nous intéressent pas (la SDL n'étant pas même nécessairement à l'origine de ces fuites, leur origine est peut-être une bibliothèque utilisée par la SDL, X11???).
Pour remédier à ce problème, Valgrind permet de supprimer certain des résultats dans ses rapports. Un ensemble de règles de suppression peut être écrit dans un fichier que l'on nomme fichier de suppressions.
Ce fichier de suppressions peut être généré à partir d'un log d'une session d'analyse avec l'option `–gen-suppressions=all`. Le principe est simple : on détecte des erreurs sur un programme qui n'a pas d'erreur, et on va indiquer à Valgrind que par la suite, ces erreurs ne doivent plus être notifiées dans les rapports.
- Attention
- tout problème détecté durant cette session sera ensuite ignoré, il faut donc s'assurer de le faire avec un programme dont on est certain de la validité !
Exécution de Valgrind avec génération des informations de suppression :
valgrind --leak-check=full --show-reachable=yes --error-limit=no --gen-suppressions=all --log-file <log> <executable>
Où :
<log>doit être remplacé par un chemin vers un fichier à écrire,<executable>doit être remplacé par le chemin vers l'exécutable à exécuter.
Un script accessible ici (qu'il ne pas oublier le rendre exécutable après l'avoir téléchargé), permet de traduire ce log en un fichier de suppressions :
cat <log>|./gen_valgrind_suppressions > sdl.sup
Ensuite, à chaque appel de Valgrind, on ajoute (en plus des options souhaitées)
--suppressions=./sdl.sup :
valgrind --suppressions=./sdl.sup <executable>
Ces explications sont extraites d'un wiki.
7.5 Bonnes pratiques
Pour conclure sur l'utilisation basique de Valgrind (ou plus précisément, a propos de l'outil par défaut de Valgrind : Memcheck), quelques bonnes pratiques.
7.5.1 Options de compilation
Pendant la phase de développement, l'option -g (pour GCC et Clang au moins)
permet d'intégrer dans l'exécutable de nombreuses informations utiles aux
outils comme gdb et Valgrind.
7.5.2 Allocations
Un seul appel à malloc (ou apparentés) par ligne permet d'identifier facilement l'allocation
qui pose problème lorsqu'une fuite de mémoire ou une erreur de lecture/écriture
est détectée.
7.5.3 Définitions
Une seule définition de variable par ligne permet d'identifier facilement quelle variable pose problème lorsqu'une variable non initialisée est utilisée en lecture.
8 Astuces
8.1 Comparer les temps d'exécution
On dispose de plusieurs façons pour mesurer les temps d'exécution d'un programme.
8.1.1 Méthodes rudimentaires
- La commande Linux
timepermet de mesurer le temps d'exécution d'une commande en ligne de commande.
time ./a.out time ls -al
- à l'intérieur du code C, insérer des affichages du temps passé. On peut s'inspirer du code suivant (src : koor.fr)
#include <stdio.h> #include <time.h> int main( int argc, char * argv[] ) { clock_t begin = clock(); // Do something // sleep( 2 ); // Wait 2 seconds, but no ticks are consumed int i; for( i=0; i<1000000000; i++ ) { } clock_t end = clock(); unsigned long millis = (end - begin) * 1000 / CLOCKS_PER_SEC; printf( "Finished in %ld ms\n", millis ); return 0; }
8.1.2 Méthodes évoluées : les profileurs
Les profileurs permettent de mesurer le temps passé dans chaque fonction du programme. Ils ont en général pour vocation de permettre de détecter, sans faire d'étude théorique, les portions du programme qui nécessiteraient des optimisations (mémoire ou temps). Ainsi, une fonction déjà optimisée peut mériter des optimisations plus avancées, voire une remise en cause de son principe, parce qu'elle est fréquemment appelée, alors qu'une autre fonction, peu appelée pourra être laissée un peu « bâclée ».
Il est à noter que la qualité des informations apportées par les profileurs est fortement liée à la qualité et au « réalisme » des instances sur lesquelles le programme est exécuté. Le but d'une étude de profilage est souvent de se placer soit dans le pire des cas (de façon à se rapprocher expérimentalement d'un temps garanti, très important en particulier dans le 'temps réel'), soit dans les cas qui seront les plus fréquents en production (ou un subtil mélange de ces deux situations).
Il existe deux grandes sortes de profileurs :
- ceux qui mesurent le temps mis en secondes sur une certaine machine, avec toutes ses caractéristiques particulières (son processeur, sa mémoire, sa carte graphique, …, les tâches qui sont lancées en même temps, etc),
- ceux qui s’exécutent sur une machine virtuelle, et où les unités de mesure sont plutôt, le nombre d'opérations effectuées, chaque opération possédant un coût. Le défaut majeur de ce type de profileur est la lenteur (de assez lent à … très très lent), son avantage est, par construction, sa quasi indépendance au matériel (quasi, car si le coûts réels des opérations sont relatifs au matériel).
Sous Linux, la première famille est représentée par gprof et la seconde par
callgrind qui est un module de valgrind (dont vous n'avez pour l'instant
utilisé que le module par défaut memcheck), que l'on utilise conjointement avec
le visualiseur kcachegrind.
gprof (tutoriel gprof) est d'accès beaucoup plus aisé que kcachegrind
(documentation cachegrind et documentation kcachegring, je ne connais pas de
tutoriel particulièrement pertinent, vous pouvez en choisir un 'au hasard', il
vous permettra à tout le moins de commencer à travailler si c'est l'outil que
vous choisissez).
8.2 clang-format
clang-format est un formateur automatique de code, il va présenter automatiquement le code, en choisissant là où il y a des espaces, combien, la position des accolades… Cela va permettre d'avoir une unité dans la façon de présenter le code, et donc aider à sa lecture et sa maintenance. Avant son utilisation, il est nécessaire de créer un ficher de configuration qui va définir le style de la présentation.
clang-format -style=LLMV -dump-config > ~/.clang-format
Le style par défaut est LLMV, mais il existe d'autres styles directement
accessibles :
- Chromium
- Mozilla
- WebKit
- Microsoft
- GNU
En plus de ces styles, il est possible de créer son propre style ex nihilo, ou en modifiant un style déjà existant.