Présentation de notre 2ème semaine !

Qu'allez-vous pouvoir lire dans cette page ?

Nous allons vous présenter dans cette page des implémentations possibles pour des nouvelles structures de données : des partitions et des tas notamment. Ensuite nous nous attaquerons à des algorithmes de parcours et de création de graphes qui vont nous permettre à terme de générer un labyrinthe et de simuler de manière artificielle la vie dedans... Bonne lecture !

Retour vers la semaine dernière...

Un chef-d'oeuvre restauré ?

En effet, il fallait bien vous présenter une deuxième version de notre jeu qui... fonctionne cette fois !

Des structures plus avancées



Structure de partitions

 
1
2
3
4
5
6
7
8
9
Au début :
Indices : 0  1  2  3  4  5  6  7  8
Tableau : 0  1  2  3  4  5  6  7  8
Hauteur : 1  1  1  1  1  1  1  1  1
 
Après les opérations :
Indices : 0  1  2  3  4  5  6  7  8
Tableau : 0  0  6  6  4  7  0  7  8
Hauteur : 3  0  0  0  1  0  0  2  1
 
  
                Au début :
                Indices : 0  1  2  3  4  5  6  7  8
                Tableau : 0  1  2  3  4  5  6  7  8
                Hauteur : 1  1  1  1  1  1  1  1  1
                
                Après les opérations :
                Indices : 0  1  2  3  4  5  6  7  8
                Tableau : 0  0  6  6  4  7  0  7  8
                Hauteur : 3  0  0  0  1  0  0  2  1

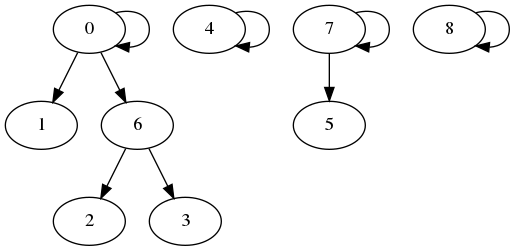
Implémentation par marqueurs

Premier type d'implémentation : avec un tableau. Exemple ci-contre avec les opérations :

 
1
2
3
4
5
fusion(parttition, hauteur, 0, 1);
fusion(parttition, hauteur, 6, 3);
fusion(parttition, hauteur, 6, 2);
fusion(parttition, hauteur, 0, 3);
fusion(parttition, hauteur, 7, 5);
 
  
fusion(parttition, hauteur, 0, 1);
fusion(parttition, hauteur, 6, 3);
fusion(parttition, hauteur, 6, 2);
fusion(parttition, hauteur, 0, 3);
fusion(parttition, hauteur, 7, 5);

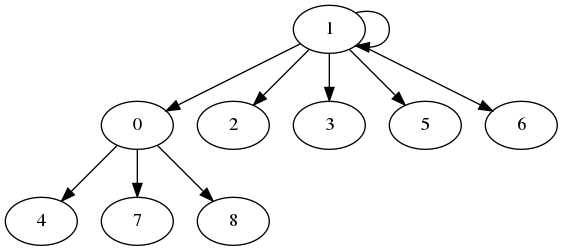
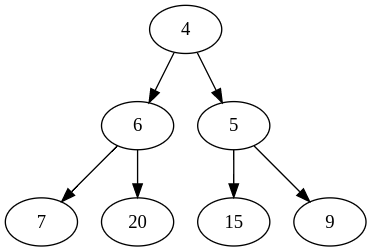
Implémentation arborescente

Ici, on reprend les mêmes données que précédemment, et chaque arbre représente une classe de la partition. Pour rappel, au début nous avons :

Arbre début

On obtient ce résultat :

Arbre fin

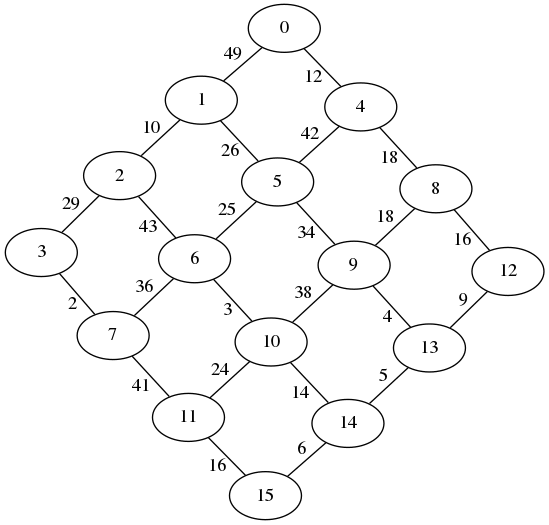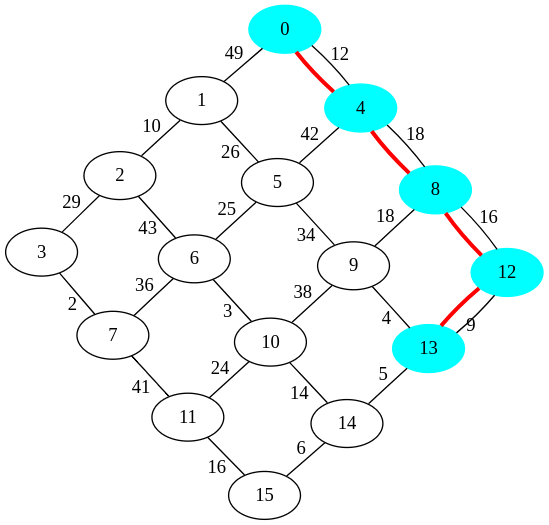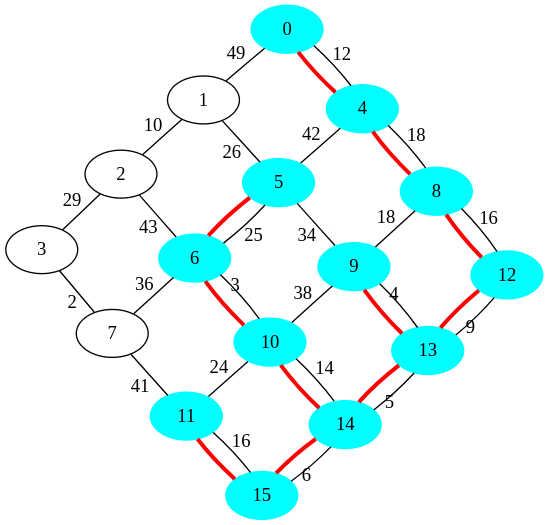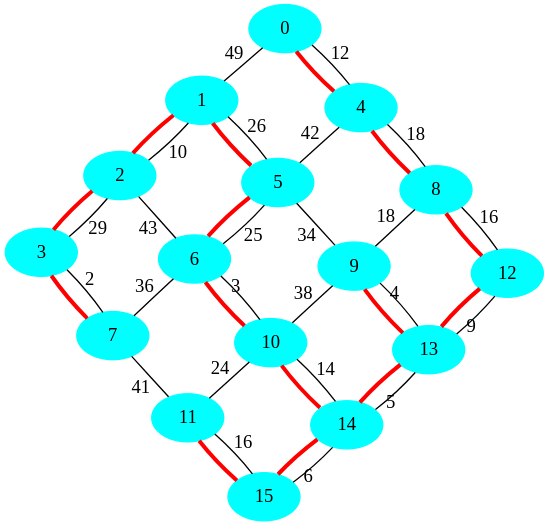
Graphe généré grâce à la matrice d'adjacence :

Matrice d'adjacence

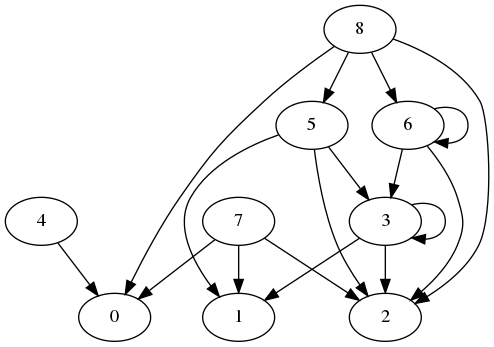
Composantes connexes de graphes aléatoires

Dans un premier temps, on génère de manière aléatoire une matrice d'adjacence. Cette matrice permet de générer le graphe ci-contre.
Ensuite, les composantes connexes sont extraites et on obtient le résultat ci-dessous :

Matrice d'adjacence

Algorithmes de parcours de graphes et génération de labyrinthes



Vers la simulation d'une vie artificielle dans un labyrinthes

Arbre couvrant de poids minimal

On va se servir de l'algorithme de Kruskal pour calculer cet arbre. On se sert également de la structure partition décrite précédemment. Vous pouvez voir ci-contre une animation générée avec Graphviz de cet algorithme. Cette forêt va nous servir par la suite à générer le labyrinthe.

Animation Kruskal

Un tas min

Tas min

Brève présentation des tas binaires

Un tas max (resp. tas min) T est un arbre binaire quasi-parfait étiquetté par des objets comparables (ie : il existe un ordre total) tel que tout noeud a une étiquette plus grande (resp. plus petite) que ces fils.
Nous avons utilisé les fonctions suivantes :

 
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
min_heapify(distances tab[], int i, int *taille)
// Complexité : log N
 
build_min_heap(distances tab[], int *taille, int taille_max)
// Complexité : N
 
heapsort(distances tab[], int taille, int taille_max)
// Complexite : N log N
 
heap_extract_min(distances tab[], int *taille)
// Complexité : log N
 
heap_increase_key(distances tab[], int i, int key)
// Complexité : log N
 
min_heap_insert(distances tab[], int key, int *taille)
// Complexité : log N
 
  
min_heapify(distances tab[], int i, int *taille)
// Complexité : log N

build_min_heap(distances tab[], int *taille, int taille_max)
// Complexité : N

heapsort(distances tab[], int taille, int taille_max)
// Complexite : N log N

heap_extract_min(distances tab[], int *taille)
// Complexité : log N

heap_increase_key(distances tab[], int i, int key)
// Complexité : log N

min_heap_insert(distances tab[], int key, int *taille)
// Complexité : log N

Algorithmes de parcours de graphe

Algorithme de Dijkstra

Cet algorithme nous permet de trouver le plus court chemin dans un graphe en utilisant une file de priorité. On connait le point de départ et le point d'arrivée.

Algorithme A* (ou A star)

C'est une variation de l'algorithme de Dijkstra, il va ordonner différemment les noeuds à explorer dans la file de priorité.
On va se servir de 3 types de distances :

  1. La distance Euclidienne
  2. La distance de Tchebychev
  3. La distance de Manhattan

Petite comparaison sur l'exécution

Résultat sur 10 essais

1 2 3 4 5 6 7 8 9 10
Dijkstra 98 56 74 52 73 81 77 84 74 97
A* Euclidienne 87 47 73 52 63 74 46 70 63 81
A* Tchebychev 87 47 73 52 66 75 49 67 63 80
A* Manhattan 91 45 71 51 52 71 47 74 64 81

Evolution du nombre de noeuds parcourus

Exploration d'un graphe en profondeur d'abord (DFS)

Contrairement aux deux algorithmes présentés précédemment, le DFS ne permet pas de trouver le plus court chemin dans un graphe (resp. dans un labyrinthe), il permet de connaitre le graphe sur lequel on est quand on commence sur le seul noeud qu'on nous a donné.

Simulation d'évolution d'une population



Élaboration d'un modèle pour étudier une population

Présentation de notre simulation

Dans cette simulation, nous étudions une population de singes avec des individus qui doivent se déplacer de points d'intérêt en points d'intérêt pour chercher leurs nourritures. L'utilisateur saisit initialement les données suivantes :

  1. La taille de leurs zones d'évolution (1 case correspond à un Ha)
  2. Le nombre de groupes d'individus au départ
  3. Leurs espérances de vie (par pas de 2 ans)

Et d'autres paramètres

Suivant les paramètres saisis, il peut y avoir plusieurs issues. Parmi toutes les possibilités, on distingue deux cas extrêmes, soit la population meurt trop rapidement, soit il y a surpopulation.

Exemple suivi de données dans le cas d'une extinction

Nous allons simuler une extinction d'espèce avec les paramètres suivants :

  1. Taille de leurs zones d'évolution : 12 Ha
  2. Nombre de groupes d'individus au départ : 7 groupes
  3. Espérance de vie (par pas de 2 ans) : 15 (soit 30 ans)

Vous pouvez voir cette simulation sur la vidéo ci-contre. Les données extraites sont disponible dans la partie suivante.

Extinction

Résultats

On constate que vers la 35ème génération il y a eu un pic de mortalité et de natalité et le nombre total de singe a commencé à décroitre. On constate également que vers la 65ème génération la courbe du nombre total de singe née est passée sous la courbe du nombre total de singes, on dit qu'à ce moment-là, la population est en déclin.

Exemple suivi de données dans un cas stable

Nous allons simuler un cas de stabilité avec les paramètres suivants :

  1. Taille de leurs zones d'évolution : 12 Ha
  2. Nombre de groupes d'individus au départ : 9 groupes
  3. Espérance de vie (par pas de 2 ans) : 17 (soit 34 ans)

Vous pouvez voir cette simulation sur la vidéo ci-contre. Les données extraites sont disponible dans la partie suivante.

Extinction

Résultats

On constate que jusqu'à la 60ème génération les courbes sont relativement proches les unes des autres et que le nombre de naissances et de morts et équivalent. La dynamique de la population est stable à ce moment. Cependant on remarque qu'à partir de la 80ème génération, la distribution du nombre de morts et de naissances devient plus chaotique et le nombre total de singes nés augmente de façon exponentielle. Si la simulation avait continué plus longtemps, il est probable que nous aurions obtenu une surpopulation.
L'introduction d'un prédateur aurait pu provoquer un effet de contrôle de cette population voire même une dynamique cyclique.