Itinéraire pour piéton sur android

Itinéraire pour piéton sur android |
 |
| Présentation | Principe général | Installation | Utilisation | Itinéraire | Principe de l'algorithme | A propos de |
| GPS Piéton est une application de navigation pour piéton en zone urbaine gratuite qui a pour avantage d’être reliée en permanence à un système de cartographie libre. Cette cartographie a été réalisée par plus d’un million d’utilisateurs volontaires et elle est donc très complète et à jour .... (OpenStreetMap). |
|
Cette application est utilisable
dans n’importe quelle ville du monde et permet, par ailleurs, en
cas de coupure de réseau durant plusieurs minutes de continuer à
guider l’utilisateur. Une
des innovations apportées par cette application est que le calcul
de l’itinéraire se fait par nos algorithmes de façon itérative
afin de rendre l’application plus dynamique et réactive.
Ce n’est donc pas une feuille de route mais un itinéraire évolutif que propose cette application. |
 |
Notons toutefois qu'il s'agit d'un outil de démonstration réalisé pendant le stage de 3ème année d'école d'ingénieur de Benjamin Vincent (financé dans le cadre du Labex IMOBS3) et des bugs résiduels peuvent subsister. Remarquons aussi que des problèmes de disponibilités des serveurs de calcul peuvent occasionnellement se produire.
|
|
Une architecture client-serveur a pour principale fonction de décharger une partie du travail de l’application sur un serveur distant afin de rendre l'application de l'utilisateur moins couteuse en espace mémoire et en CPU. Une telle architecture nécessite une connexion réseau importante et donc les problèmes de connexion réseau entre l'application et le serveur peuvent altérer son bon fonctionnement. Afin de palier, autant que faire se peut à ce problème, notre architecture comprend une gestion de cette perte de connexion pour peu qu'elle soit temporaire.
|
|
A cette architecture nous avons rajouté quelques éléments afin de palier aux coupures de réseau comme l'illustre la figure ci-dessous:
|
|
L'API utilisée par le téléphone pour le dialogue avec le serveur est une API ouverte. Les programmeurs peuvent consulter : http://www.isima.fr/~lacomme/ORWebServices/GPS4pedestrian/index.php
|
|
Nota Bene : Cette
application nécessite une version android 3.0 ou plus. (api niveau
11+)
|
| Il suffit ensuite d’installer sur votre mobile l’application à partir du fichier téléchargé : | 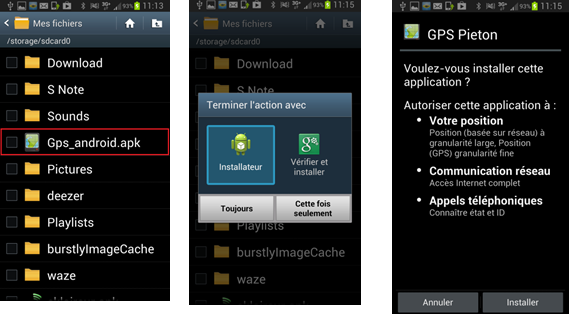 |
| L’application nécessite d’activer le gps et les données mobiles du téléphone : | 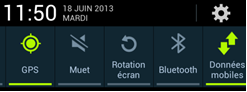 |
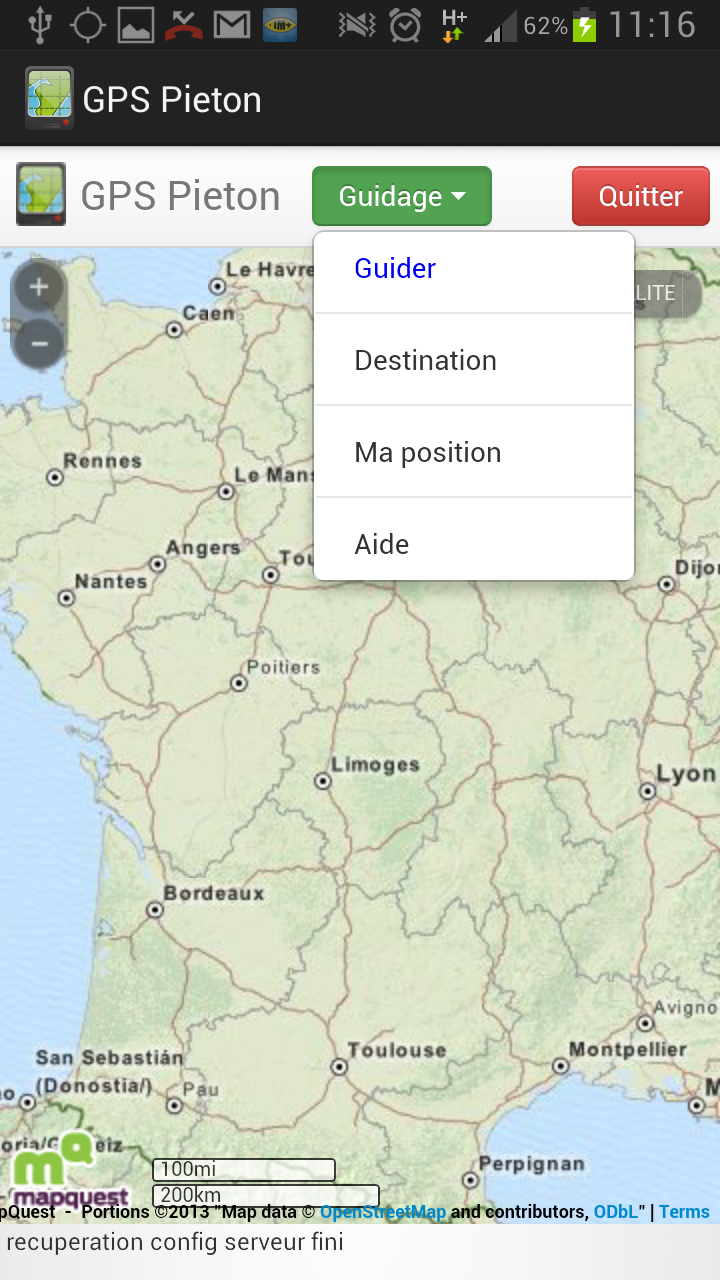
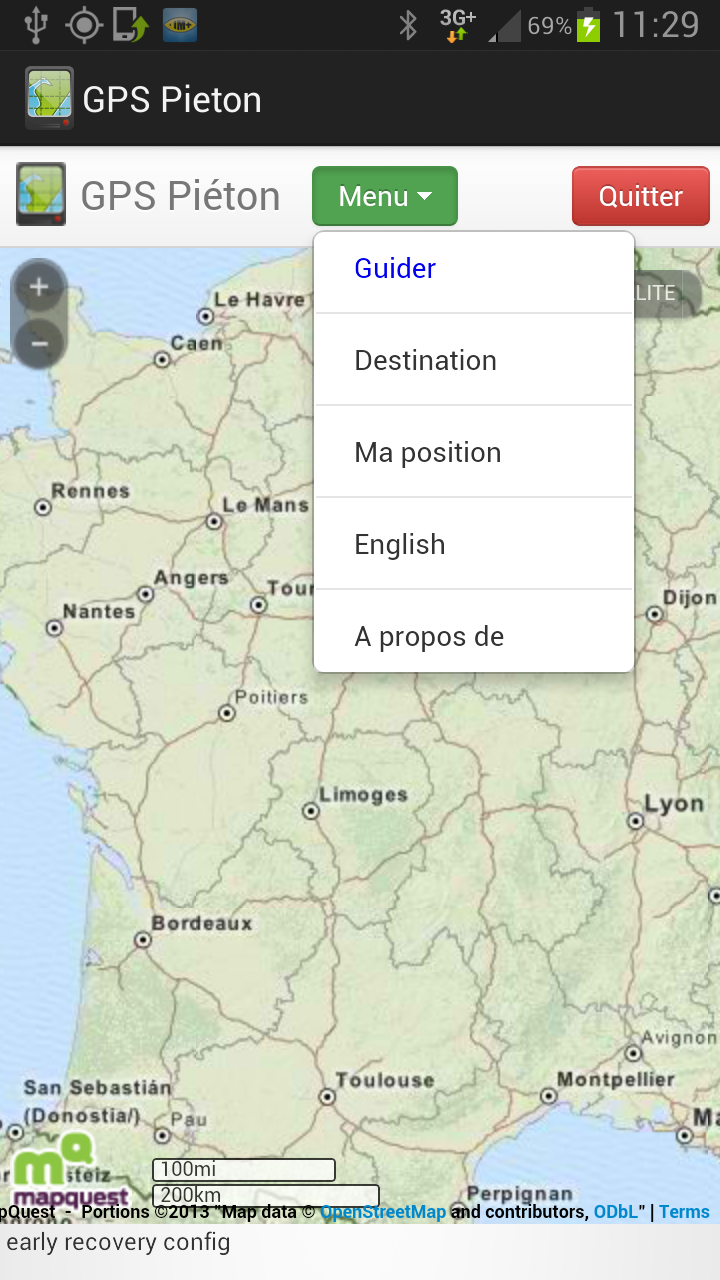
Les différentes fonctionnalités de l’application sont disponibles à partir du menu. |
 |
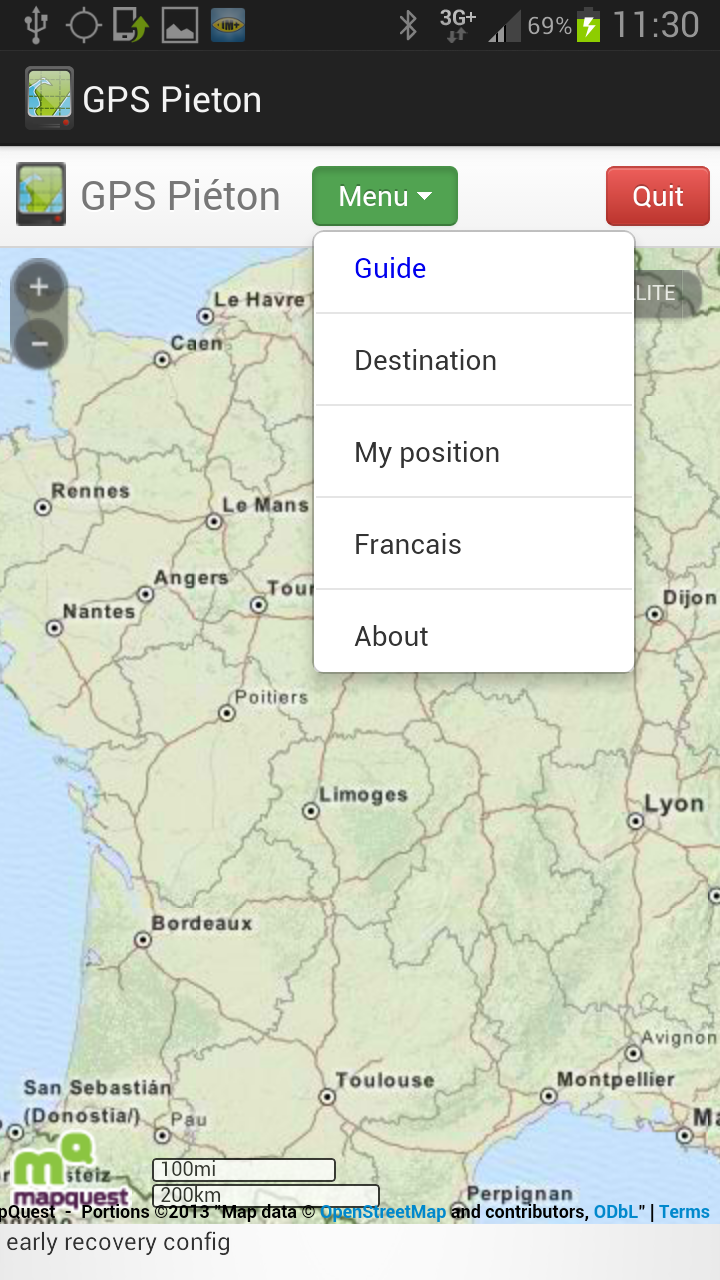
| Ma position : Centre la
carte sur la position GPS actuelle
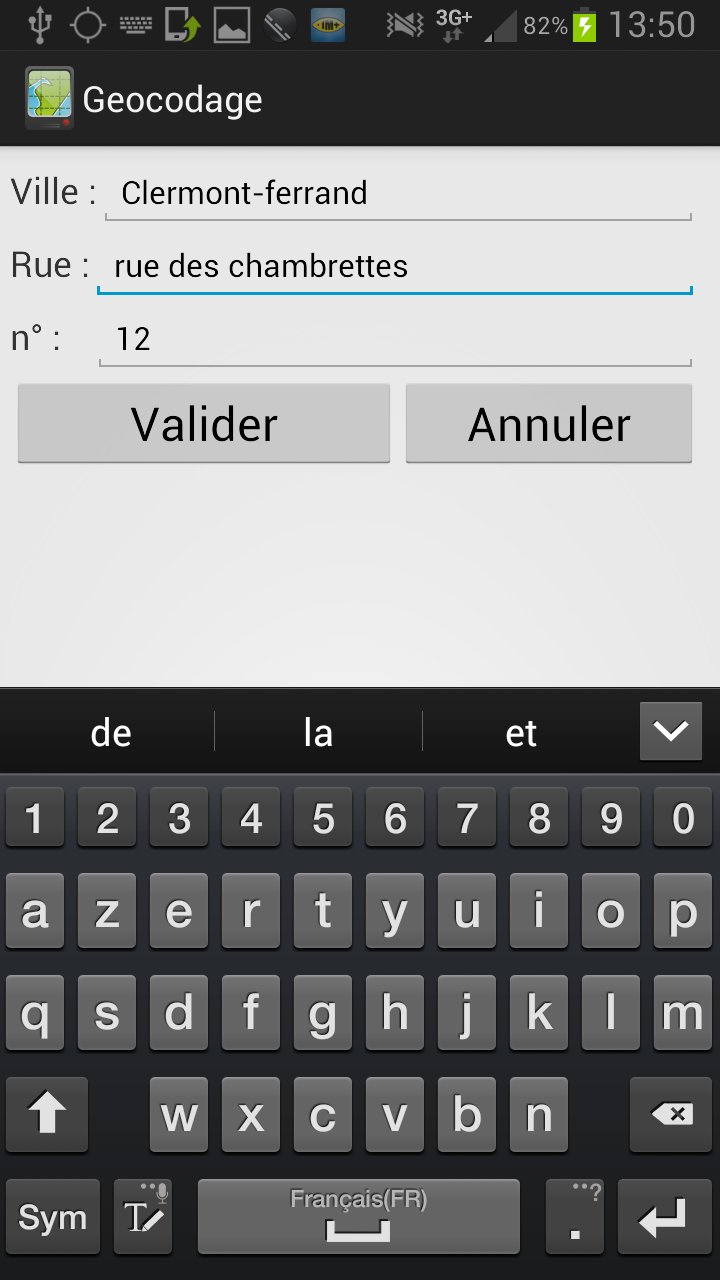
Destination : Permet de saisir l’adresse postale de la destination souhaitée |
 |
 |
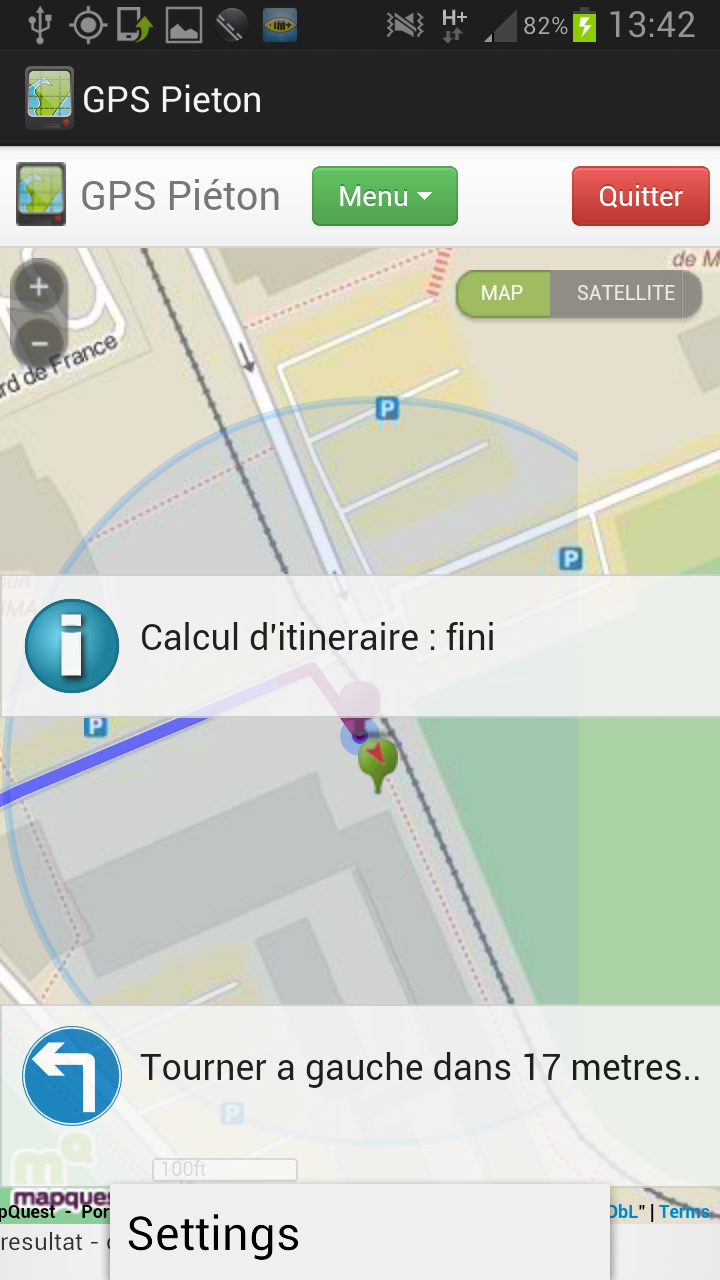
| Guider : permet de lancer le calcul d’itinéraire une fois que la destination souhaitée a été rentrée | |
 |
| La langue : qui permet de passer
l’application en anglais ou en français. (la langue par défaut
correspond à la langue du téléphone. A propos de : Quelques informations sur la conception de l’application |
 |
 |
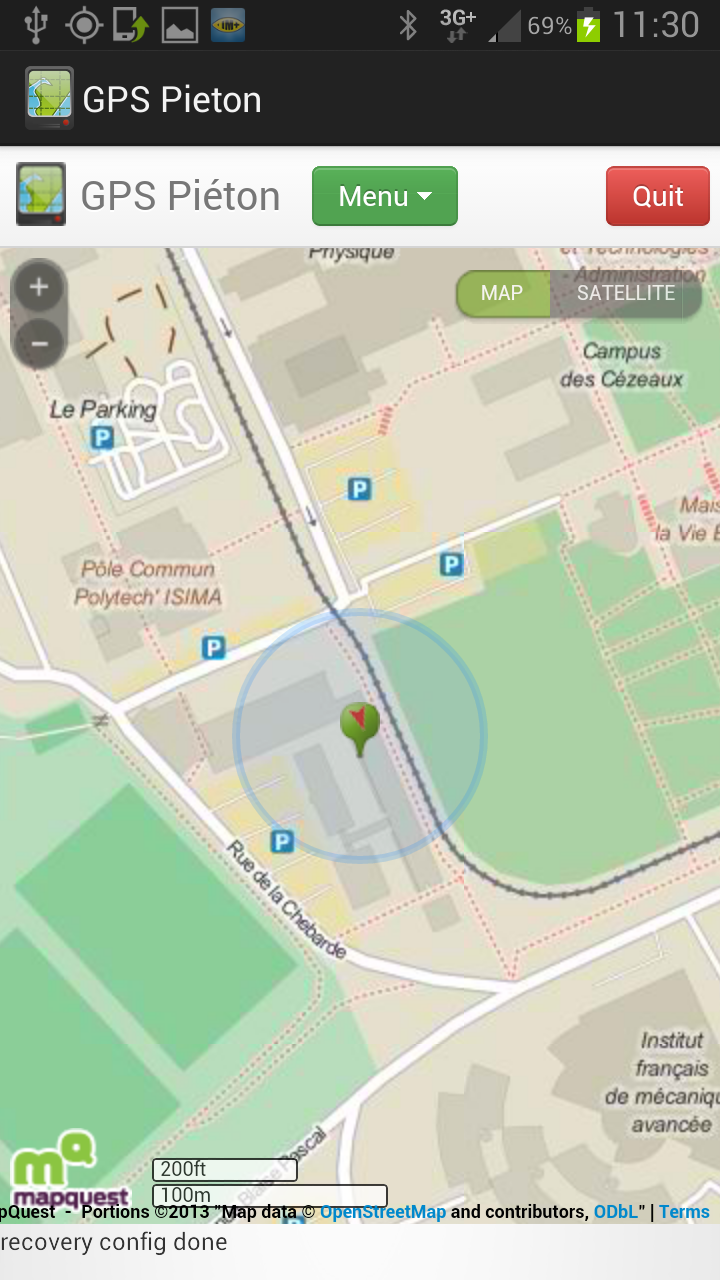
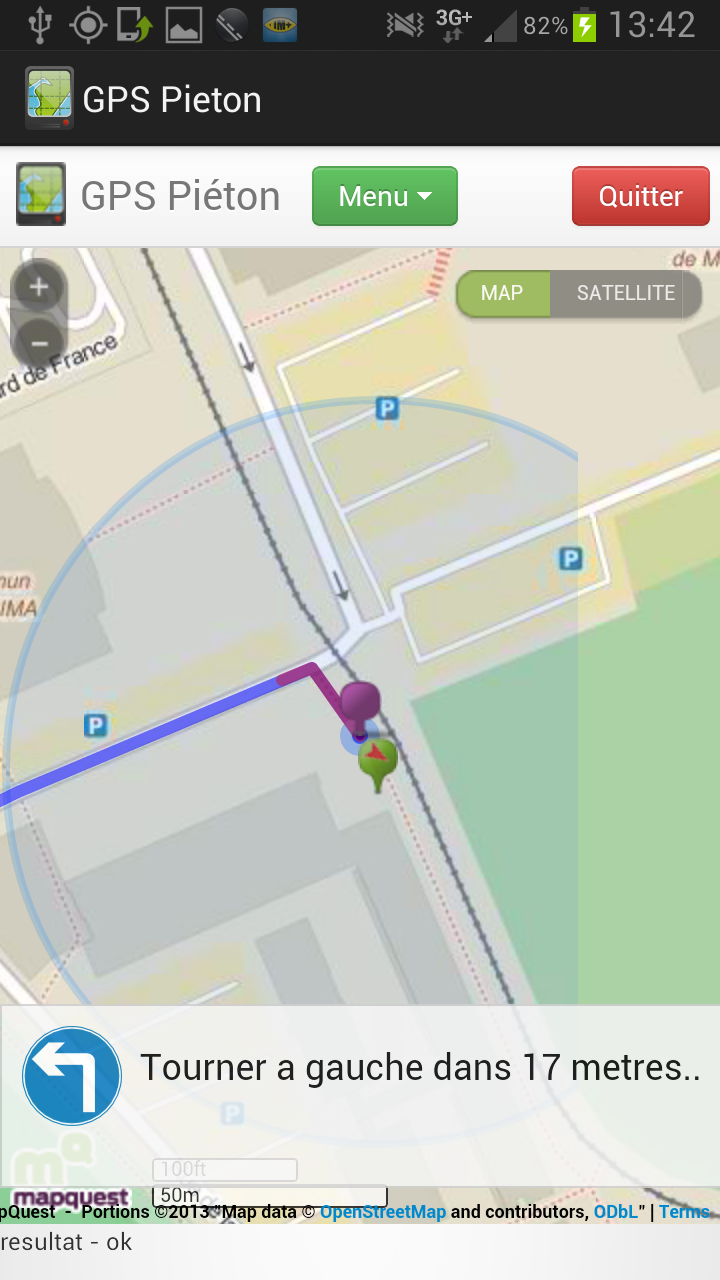
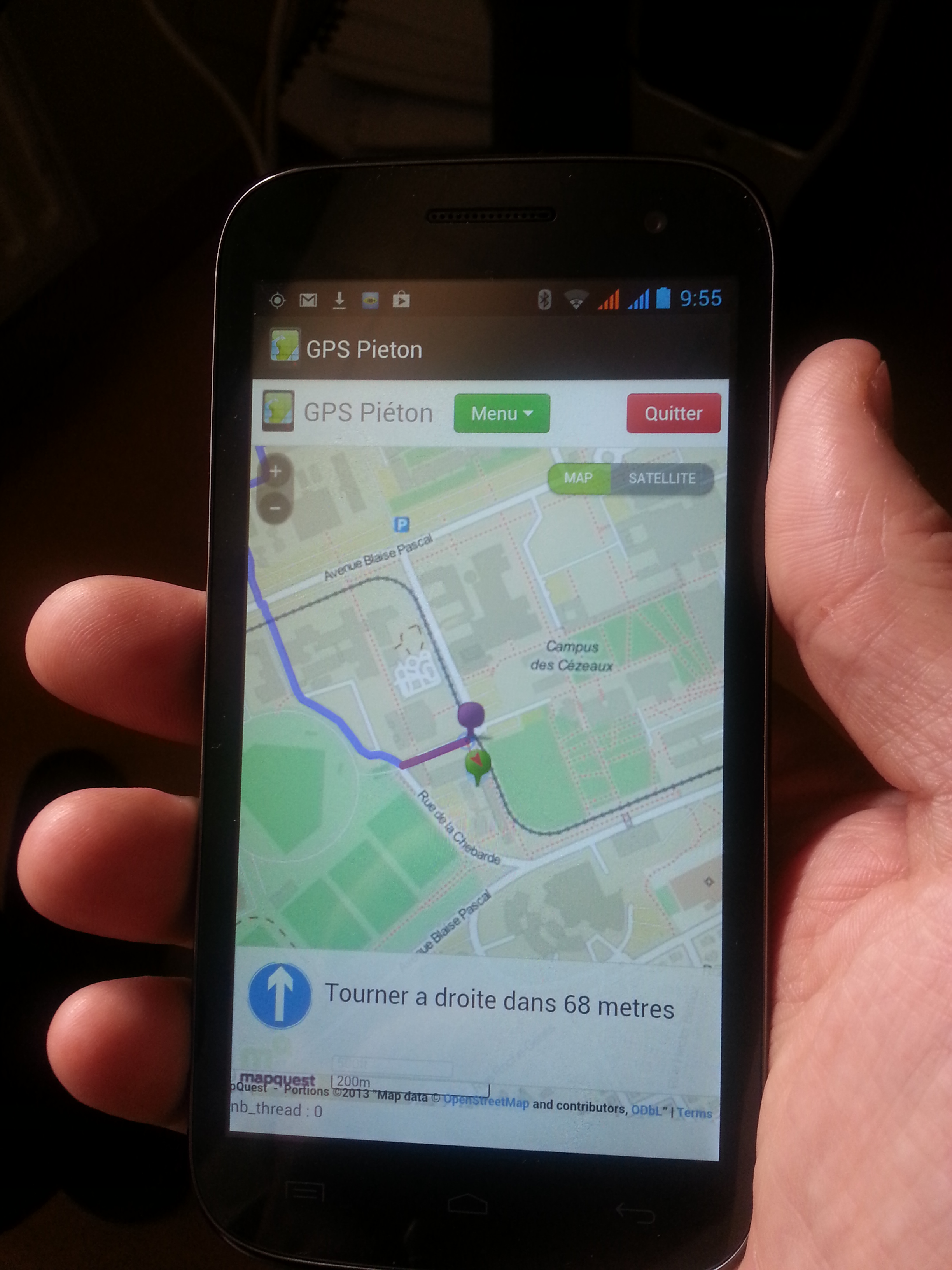
| Le calcul de l’itinéraire se fait de façon itérative. C’est-à-dire qu’il se construit au fur à mesure qu’on le parcourt. Sur l’exemple ci-joint, en dé-zoomant la carte suffisamment, on remarque que l’itinéraire n’est pas complet (le point vert, en haut à gauche, représente la destination), il se finira lorsque l’utilisateur aura parcouru une partie du premier itinéraire proposé. | 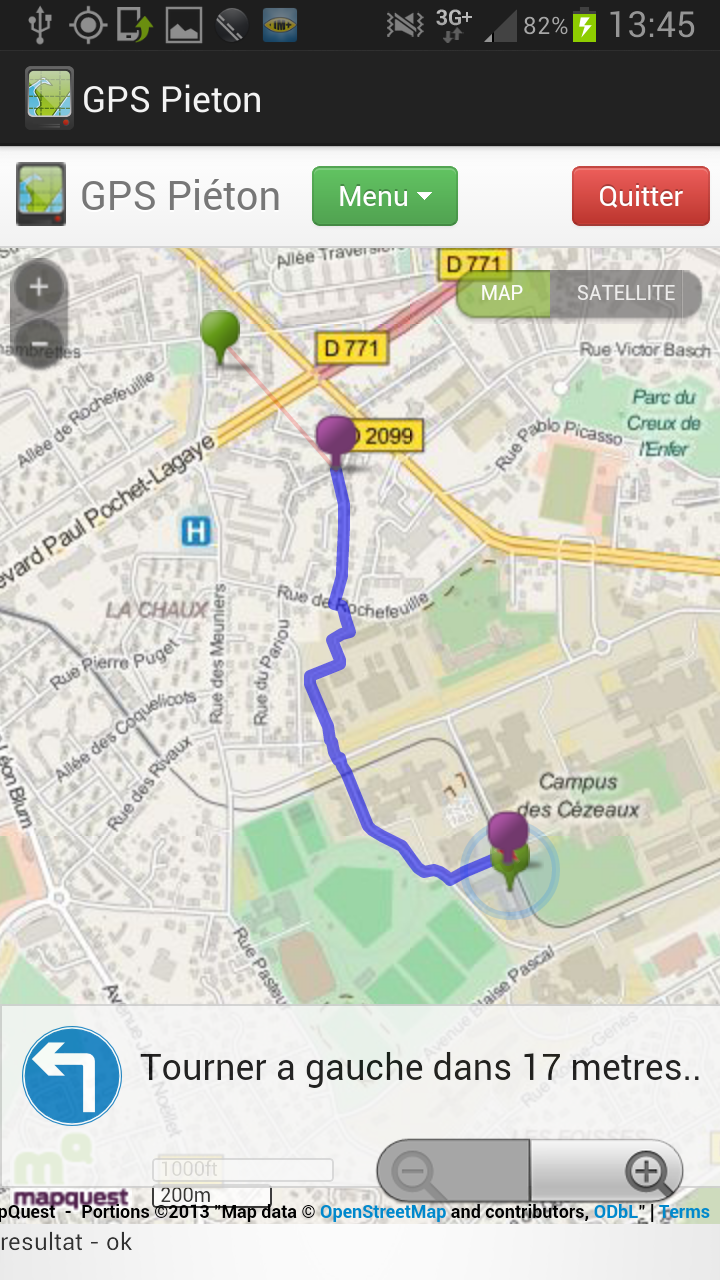 |
|
On peut assimiler un réseau routier
à un graphe connexe et acyclique où les noeuds représentent
les points d'intérêts du réseau (comme les intersections de
plusieurs rues par exemple) et où les arrêtes représentent les
routes liants ces points d'intérêts.Le nombre d'arrêtes dans
un tel graphe est alors de même ordre que son nombre de
noeuds(en moyenne 2 à 3 fois supérieur en zone urbaine).
Parmi les algorithmes de plus cours chemin, on peut citer par exemple l'algorithme de Disjkstra (Dijkstra, 1959) dédié aux graphes acycliques à valeurs positives ou l'algorithme de Bellman qui lui permet de traiter des graphes à valeurs quelconques. De nombreux algorithmes ont été comparés sur des critères variés dont en particulier leur efficacité en temps de calcul. On peut consulter par exemple, l'article, un peu ancien mais très intéressant de Bruce Golden (Golden , 1976). Pour des informations liées à la complexité des différents algorithmes, on peut se reporter à (Pallottino, 1984). Des dernières années, de nombreux auteurs se sont intéressés à l'extention de ces algorihtmes afin de traiter (dans des temps raisonnables) des graphes de très grandes tailles. Par exemple, on peut citer (Gerhard, 1998). On peut trouver dans (Wagner and Willahalm, 2003) (Wagner and Willahalm, 2005) une description très précise de nombreuses techniques tirant profit de l'aspect géométrique. On peut trouver la description d'autres techniques, par exemple de décomposition dans (Jung and Pramanik, 2012). |
|
Afin d'illuster notre propos, nous
rappelonsici les principes de l'algorithmes de Dijstra.
C’est un algorithme itératif dans lequel l’information sur la distance parcourue depuis le point de départ est propagée de voisin en voisin jusqu’au point d’arrivée. Le temps d'éxécution de cet algorithme dépend donc fortement du nombre de sommets sur lesquels sont propagés les libélés. Dans la mise en oeuvre de cet algorithme, on peut remarquer : 1) qu'il est possible de stopper la propagation des libels lorsque le nœud du graphe avec le plus petit label non traité correspond au nœud final. 2) qu'on peut limitater du nombre de sommets, étape de prétraitement du graphe : telle astuce consiste à limiter la taille du graphe avant de lancer l’algorithme. Le principe de cette étape repose sur le fait que le graphe routier en zone urbaine est suffisamment dense pour estimer que le trajet effectué par un piéton se rapproche de la ligne droite. On délimite alors une zone ellipsoïdale de taille raisonnable (c’est-à-dire de façon à garder la connexité entre le point de départ et d’arrivée) autour de cette ligne droite afin de limité la taille de notre graphe initial. 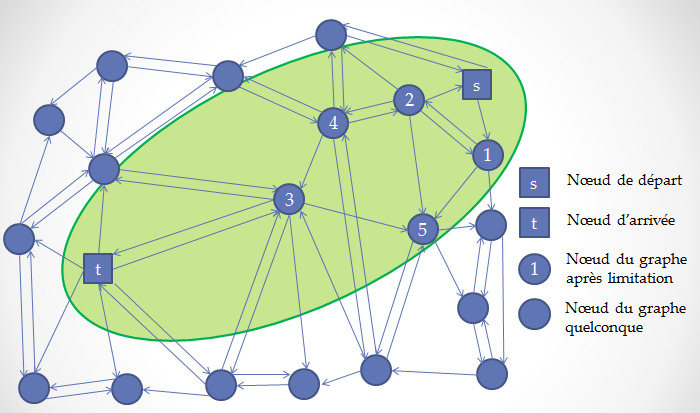 |
|
Notons
que les astuces de limitation du nombre de sommets et de
contraction du graphe ne garantissent pas l'optention de la
solution optimale mais que les cas où l'on diverge de l'optimal
par ce procédé sont extrèmements rares en milieu urbain. De
plus, on s'assure de garder la connexité entre le point de
départ et d'arrivée afin de donner dans tous les cas un
itinéraire valide.
Calcul itératif du chemin : Cette dernière astuce sert principalement à pallier au problème de la gestion de l'éloignement de l'utilisateur de l'itinéraire (pour cause d'imprévus du réseau routier non-référencés sur notre graphe, comme les accidents et les travaux par exemple, ou par erreur de l'utilisateur). Nous avons, pour ce faire, calculer le chemin de façon plus dynamique afin de faciliter le recalcul dans le cas où le piéton dévie de sa trajectoire. Le principe réside dans le fait que l’on n’a pas besoin pour se diriger sur une route de l’ensemble de l’itinéraire mais seulement des quelques prochaines instructions. La méthode consiste donc à ne calculer qu’une partie de l’itinéraire (environ 1km et demi) afin de rendre le calcul plus rapide et donc plus réactif aux changements imprévus. Le calcul consiste, comme pour la technique de la limitation du graphe, à tracer une droite entre le point de départ et d’arrivée afin d’obtenir la direction que l’on doit suivre et donc d’établir un premier point de passage. Le calcul est alors réitéré dans deux cas, le cas où l’utilisateur s’éloigne du chemin pré-calculé et le cas où l’on est à une distance raisonnable de la fin du premier morceau d’itinéraire afin d’éviter le cas du "cul de sac". 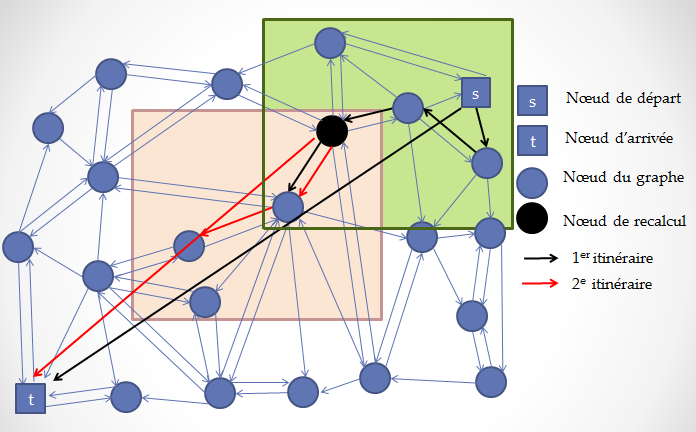 Notons qu’en se servant de cette
méthode, on perd en moyenne 5% d’optimalité sur le plus court
chemin dû à l'effet escalier qu'elle peut engendrer. Cette erreur
représente un rajout d'une centaine de mettres sur un itinéraire
de deux kilomètres de long, ce qui est négligeable dans un cas
concret d'utilisation.
|
|
Dijkstra E.W. A note on two problems in Connexion with graph. Numerische Mathematik, Vol. 1, pp. 269-271. 1959. Golden B. Shortest Path Algorithms: A comparison. Operations Research, Vol. 24(6), 1976. Pallottino S. Shortest-Path methods: complexity, interrelations and new propositions. Networks. Vol 14(2). 1984. Gerhard Ert. Shortest Path calculation in large road networks. OR Spektrum. Vol 20. pp. 15-20. 1998. Wagner F. and T. Willahalm. Geometric Speed-Up Techniques for Finding Shortest Paths in Large Sparce Graphs. Konstanzer Scheriften in Mathematik. N. 183. ISSN: 1430-3558. 2003. Willahalm T. Engineering Shortest Paths and Layout Algorithms for Large Graphs. Dissertation. Doktors der Naturwissenschaften der Fakultat fur Informatik der Universitat Fridericiana zu Karlsruhe. 2005. Jung S. and Pramanik S. An Efficient Path Computation Model for Hierarchical Structured Topographical Road Maps. IEEE Transactions onKnowledge and Data Engineering. Vol. 14(5), October 2012. Wagner D. and Willahalm T. Geometric Containers for Efficient Shortest-Path Computation. ACM Journal of Experimental Algorithmics. Vol 10 (1.3.). pp. 1-30. 2005. |
Téléphone Samsung Galaxy Note II
|
 |
Téléphone WIKO Cink Five
|
 |
Téléphone ACER V360
|
 |
AuteursBenjamin VINCENTbenjamin.vincent023@gmail.com Encadrement du stage :Libo REN Remerciements :Merci aux ingénieurs de l'ISIMA pour leur aide pendant ce projetFinancements :Le stage de Benjamin Vincent a été financé dans le cadre du LABEX IMOB S3
Encadrement du stage :Site accès développeur sur lequel est présenté le web service de calcul d'itinéraire est sur le lien : lien du site(Ce site contient, entre autre, le code source de notre application android et de notre web service de calcul d'itinéraire.) InformationsCartographie : Mapquest et OpenStreetMapCalcul du plus court chemin : LIMOS Hébergement : LIMOS Serveur JEE : Glassfish |