Minimax exercice
Table of Contents

1. Doxygene
2. Sujet
2.1. Introduction Minimax exercice
On nous propose un jeu à somme nulle à 2 joueurs, où les joueurs alternent leurs tours. Le jeu dure toujours D tours, et lors de son déplacement, chaque joueur doit choisir parmi B choix. Ainsi, D est la profondeur de l’arbre du jeu, B son facteur de branchement, et selon les choix des joueurs, le jeu a B ^ D résultats possibles.
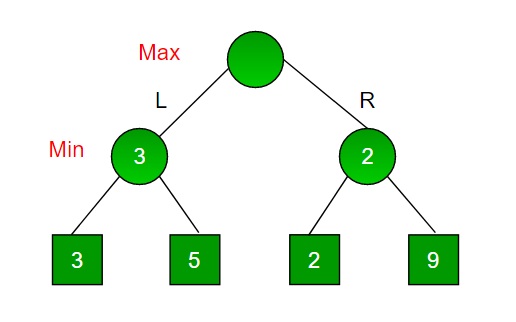
2.2. Introduction Minimax simple example
Au début les 2 joueurs voient une pile de lettres toutes différentes. À tour de rôle, ils peuvent choisir d’obtenir la première ou la deuxième lettre de la pile. Au dernier tour, le dernier joueur n’a d’autre choix que de récupérer la dernière lettre. Ensuite, les joueurs marquent des points en fonction des mots qu’ils peuvent construire avec leurs lettres collectées. Un dictionnaire donne les mots possibles avec leurs gains associés. Les lettres peuvent être utilisées plusieurs fois pour former plusieurs mots.
Vous devez conseiller le premier joueur pour son premier tour : quelle lettre est la meilleure à choisir et quels scores sont attendus pour chaque joueur, lorsque les deux joueurs jouent leur meilleur choix à chaque tour.
3. Solution expliquée
3.1. Minimax exercice
Je crée une structure noeud comprenant la valeur du noeud son nombre d’enfants ainsi que un tableau de pointeur sur d’autres structure noeud qui representent les enfants du noeud actuel
typedef struct node{ int valeur; int nbenfant; struct node *enfant[5]; } node;
Je crée deux fonction min et max qui me permet de renvoyer la valeur min ou max entre deux valeurs
int max(int a, int b) { if(a>b) { return a; } return b; } int min(int a, int b) { if(a>b) { return b; } return a; }
Ici je code une fonction createNode() qui va me permetre de crée un arbre avec ma structure node selon la profondeur et le nombre de branches souhaite. Les noeuds de cette structure seront alors alouer dynamiquement grace aux malloc. Puis elle va venir inserer les valeurs des feuilles dans les nodes les plus profonde.
void createNode(node *nodeMaman,int profondeur,int nbBranches,int liste[],int nbFeuilles) { if(profondeur>1) { for(int i =0;i<nbBranches;++i) { node *PnewNode=malloc(sizeof(*PnewNode)); PnewNode->valeur=0; PnewNode->enfant[0]=NULL; PnewNode->enfant[1]=NULL; PnewNode->enfant[2]=NULL; PnewNode->enfant[3]=NULL; PnewNode->enfant[4]=NULL; nodeMaman->enfant[i] = PnewNode; createNode(PnewNode,profondeur-1,nbBranches,liste,nbFeuilles); } } else if(profondeur==1) { for(int i =0;i<nbBranches;++i) { for(int y=0;y<nbFeuilles;++y) { if(liste[y]!=2000) { node *PnewNode=malloc(sizeof(*PnewNode)); PnewNode->valeur=liste[y]; nodeMaman->enfant[i] = PnewNode; PnewNode->nbenfant=nbFeuilles; PnewNode->enfant[0]=NULL; PnewNode->enfant[1]=NULL; PnewNode->enfant[2]=NULL; PnewNode->enfant[3]=NULL; PnewNode->enfant[4]=NULL; liste[y]=2000; break; } } } } }
Je crée ensuite une fonction recursive alphabeta qui va faire remonter la valeur la plus haute que le joueur alpha est garanti d’avoir peut importe ce que le joueur beta joue. Cette fonction va donc parcourir les noeuds precedement cree de fa9on inteligente puisque elle va eviter de passer dans toutes les feuilles si la feuille voisine est deja une borne min ou max selon le alpha ou beta actuel. J’ai aussi ajouter un compteur qui va modifier de par un pointeur la valeur d’une variable afin de compter le nombre de noeuds parcouru.
int alphabeta(node *node,int depth,int alpha,int beta, bool maximizingPlayer,int nbBranches,int *Compteur) { *Compteur=*Compteur+1; if(depth == 0 || node->enfant[0]==NULL) { return node->valeur; } if( maximizingPlayer) { int value = -999999; for(int i=0;i<nbBranches; ++i) { value = max(value, alphabeta( node->enfant[i], depth - 1, alpha, beta, false,nbBranches,Compteur)); if( value >= beta ) { break; } alpha = max(alpha, value); } return value; } else { int value = 999999; for(int i=0;i<nbBranches; ++i) { value = min(value, alphabeta(node->enfant[i], depth - 1, alpha, beta, true,nbBranches,Compteur)); if (value <= alpha ) { break; } beta = min(beta, value); } return value; } }
Enfin je crée une fonction freeNode() recursive afin de liberer correctement chaques noeuds du malloc a la fin de mon programme.
void freeNode(node* root) { if (root == NULL) { return; } // Libérer récursivement chaque enfant for (int i = 0; i < root->nbenfant; ++i) { freeNode(root->enfant[i]); } // Libérer le nœud lui-même free(root); }
Et voici le main qui va venir convertir les input dans des variables plus facile a utiliser, elle va aussi créer la premiere node mere de notre arbre et faire apelle aux fonction vu au dessus
int main() { int D; int B; int ListeDeFeuille[40001]; int CompteurDeNoeuds =0; int *PCompteurDeNoeud=&CompteurDeNoeuds; int min=0; scanf("%d%d", &D, &B); fgetc(stdin); char LEAFS[40001]; scanf("%[^\n]", LEAFS); int index = 0; // Tokenizer pour séparer les valeurs char *token = strtok(LEAFS, " "); // Convertir chaque token en entier et les stocker dans la liste while (token != NULL) { ListeDeFeuille[index++] = atoi(token); token = strtok(NULL, " "); } node node0 ={0,B,{NULL,NULL,NULL,NULL,NULL}}; node *Pnode0=&node0; createNode(Pnode0,D,B,ListeDeFeuille,index); min = alphabeta(Pnode0,D,-1000,1000,true,B,PCompteurDeNoeud); printf("%d %d\n",min,CompteurDeNoeuds); for(int z;z<B;++z) { freeNode(node0.enfant[z]); } return 0; }
Le code en entier:
#include <stdlib.h> #include <stdio.h> #include <string.h> #include <stdbool.h> /** * Auto-generated code below aims at helping you parse * the standard input according to the problem statement. **/ typedef struct node{ int valeur; int nbenfant; struct node *enfant[5]; } node; int max(int a, int b) { if(a>b) { return a; } return b; } int min(int a, int b) { if(a>b) { return b; } return a; } int alphabeta(node *node,int depth,int alpha,int beta, bool maximizingPlayer,int nbBranches,int *Compteur) { *Compteur=*Compteur+1; if(depth == 0 || node->enfant[0]==NULL) { return node->valeur; } if( maximizingPlayer) { int value = -999999; for(int i=0;i<nbBranches; ++i) { value = max(value, alphabeta( node->enfant[i], depth - 1, alpha, beta, false,nbBranches,Compteur)); if( value >= beta ) { break; } alpha = max(alpha, value); } return value; } else { int value = 999999; for(int i=0;i<nbBranches; ++i) { value = min(value, alphabeta(node->enfant[i], depth - 1, alpha, beta, true,nbBranches,Compteur)); if (value <= alpha ) { break; } beta = min(beta, value); } return value; } } void createNode(node *nodeMaman,int profondeur,int nbBranches,int liste[],int nbFeuilles) { if(profondeur>1) { for(int i =0;i<nbBranches;++i) { node *PnewNode=malloc(sizeof(*PnewNode)); PnewNode->valeur=0; PnewNode->enfant[0]=NULL; PnewNode->enfant[1]=NULL; PnewNode->enfant[2]=NULL; PnewNode->enfant[3]=NULL; PnewNode->enfant[4]=NULL; nodeMaman->enfant[i] = PnewNode; createNode(PnewNode,profondeur-1,nbBranches,liste,nbFeuilles); } } else if(profondeur==1) { for(int i =0;i<nbBranches;++i) { for(int y=0;y<nbFeuilles;++y) { if(liste[y]!=2000) { node *PnewNode=malloc(sizeof(*PnewNode)); PnewNode->valeur=liste[y]; nodeMaman->enfant[i] = PnewNode; PnewNode->nbenfant=nbFeuilles; PnewNode->enfant[0]=NULL; PnewNode->enfant[1]=NULL; PnewNode->enfant[2]=NULL; PnewNode->enfant[3]=NULL; PnewNode->enfant[4]=NULL; liste[y]=2000; break; } } } } } void freeNode(node* root) { if (root == NULL) { return; } // Libérer récursivement chaque enfant for (int i = 0; i < root->nbenfant; ++i) { freeNode(root->enfant[i]); } // Libérer le nœud lui-même free(root); } int main() { int D; int B; int ListeDeFeuille[40001]; int CompteurDeNoeuds =0; int *PCompteurDeNoeud=&CompteurDeNoeuds; int min=0; scanf("%d%d", &D, &B); fgetc(stdin); char LEAFS[40001]; scanf("%[^\n]", LEAFS); int index = 0; // Tokenizer pour séparer les valeurs char *token = strtok(LEAFS, " "); // Convertir chaque token en entier et les stocker dans la liste while (token != NULL) { ListeDeFeuille[index++] = atoi(token); token = strtok(NULL, " "); } node node0 ={0,B,{NULL,NULL,NULL,NULL,NULL}}; node *Pnode0=&node0; createNode(Pnode0,D,B,ListeDeFeuille,index); min = alphabeta(Pnode0,D,-1000,1000,true,B,PCompteurDeNoeud); printf("%d %d\n",min,CompteurDeNoeuds); for(int z=0;z<B;++z) { freeNode(node0.enfant[z]); } return 0; }
3.2. Minimax Simple Example
Je ne suis malheuresement pas arriver à résoudre ce problème.
4. Tests et exécutions
4.1. MiniMax exercice
4.1.1. exemple de Test
Test avec comme entrées
gcc -Wextra -Wall -Werror minmax.c ./a.out 1 4 2 -1 3 0
voici le résultat:
3 5
5. Solutions de la communauté
5.1. MiniMax exercice
Dans la solution de MJZ, l’auteur reprends le principe de Alpha Beta mais il a optimisere le code a fond en prenant les inputs directement dans sa fonction ab (alpha beta), ce qui lui permet d’avoir une seule fonction au total. Il utilise aussi des variables global afin de ne pas s’embeter avec des pointeur.
#include <stdio.h> int D, B, nodes = 0; int ab(int depth, int cut, int alpha, int beta) { int value, x = depth % 2 ? 10000 : -10000; if(!cut) nodes++; if(depth == D) scanf("%d", &x); else for(int i = 0; i < B; i++) { value = ab(depth + 1, cut, alpha, beta); if(depth % 2 == 0) { if(value > x) x = value; if(x > alpha) alpha = x; } else { if(value < x) x = value; if(x < beta) beta = x; } if(alpha >= beta) cut = 1; } return x; } int main() { scanf("%d%d", &D, &B); fgetc(stdin); int best = ab(0, 0, -10000, 10000); printf("%d %d\n", best, nodes); return 0; }