X-Fenêtré

---

Principe

Cet exercice avait pour but de nous faire créer des fenêtres, de les déplacer et de les fermer, en manipulant la SDL2.

Démarche

Ici on explique notre démarche sur l'approche de cet exercice

Explications

Ici on explique notre démarche sur l'approche de cet exercice

Code

Ici on explique notre démarche sur l'approche de cet exercice

Détail par personne

Ici on explique notre démarche sur l'approche de cet exercice

---

Pavé de serpents

---

Principe

Cet exercice avait pour but de nous faire manipuler les fonctions de bases au niveau des rendus dans une fenêtre, en manipulant des formes, des couleurs ...

Démarche

Ici on explique notre démarche sur l'approche de cet exercice

Explications

Ici on explique notre démarche sur l'approche de cet exercice

Code

Ici on explique notre démarche sur l'approche de cet exercice

Détail par personne

Ici on explique notre démarche sur l'approche de cet exercice

---

Jeu de la vie

Automate cellulaire dont les règles ont été définies par J. Conway en 1970.

---

Principe

L'état de l'automate à l'étape n se crée en fonction de l'état à l'étape n-1.
L'évolution de l'état d'une cellule dépend de ses huit états voisins les plus proches.
Les règles:
* A l'étape suivante, l'étape n-1 occupera une cellule vide avec seulement 3 cellules adjacentes. (Naissance liée à l'environnement optimal)
* Les cellules qui sont occupées au niveau n-1 et qui ont deux ou trois cellules adjacentes sont conservées au niveau n. Sinon, il sera vide. (Mort due à la désertification ou à la surpopulation)

Démarche algorithmique

Mort et naissance des cellules :
On utilise un tableau de booléens SURVIE, en fonction du nombre de voisins cellulaires, pour mettre en forme les règles de survie d'une cellule et un tableau NAISSANCE similaire pour mettre en forme les règles de naissance d'une cellule.

D'un point de vue algorithmique cette fois-ci on va donc utiliser des 0 ou des 1 en contenu du tableau pour représenter nos booléens.
A chaque nouveau tour, le nombre calculé de voisins est en réalite l'indice-1 de la case du tableau à regarder pour obtenir la règle.

Sauvegarde et chargement :
Sauvegarde sous forme matricielle de la grille dans un fichier texte en appuyant en jeu sur la touche s.
Chargement durant la phase de choix des premières cellules en appuyant sur la touche l pour réutiliser le fichier texte et charger la configuration de jeu.

Comment jouer ?

1. Vous êtes au menu, choisissez entre les deux modes : Monde délimité Monde thorique
2. Vous arrivez maintenant sur une page blanche. Vous pouvez soit placer les premières cellules à votre guise à l'aide de la souris ou alors appuyer sur la touche l pour charger une configuration fichier texte existante.
3. Si vous avez choisi de placer les cellules par vous-même, appuyez sur espace pour lancer le jeu de la vie.
4. Vous voyez maintenant le jeu se dérouler sous vos yeux et vous ralentir le processus en appuyant sur la flèche du bas ou alors l'accelérer avec flèche du haut.
5. Cas possibles :
* Si le monde devient vide alors le message "cycle" sera écrit.
* Si le monde devient stable et ne bouge plus alors le message "monde stable" sera écrit. Dans les deux cas quittez le jeu en appuyant sur la croix pour fermer la fenêtre.

Code

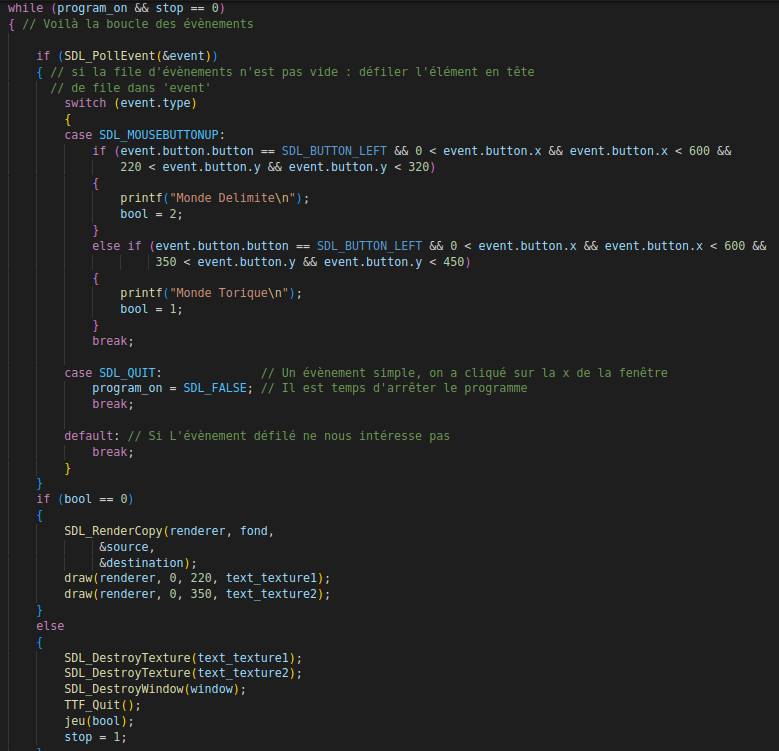
Boucle de menu

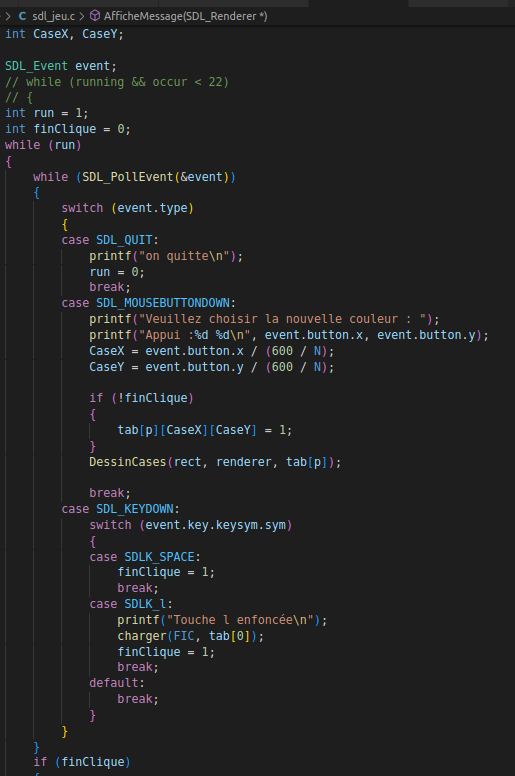
Algo Clique 1

Algo Clique 2

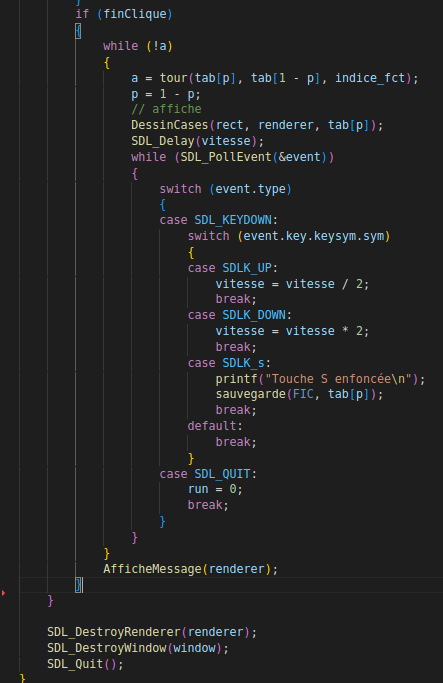
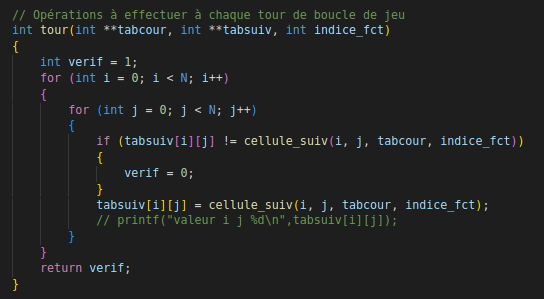
Fonction tour

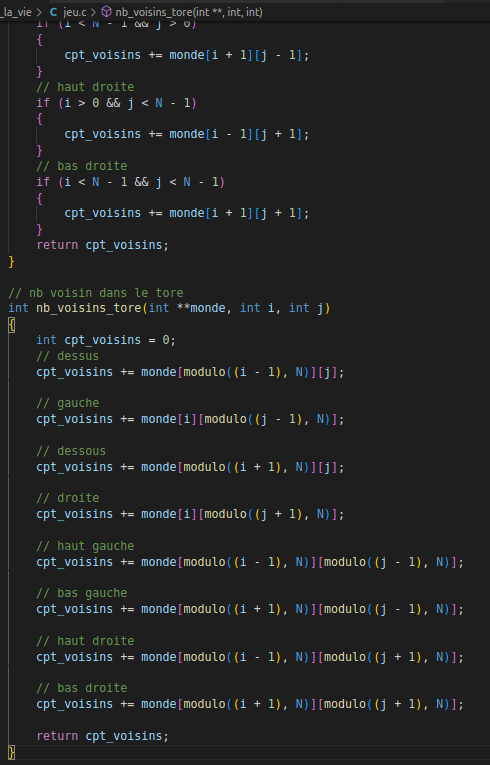
Fonctions calcul nombres de voisins

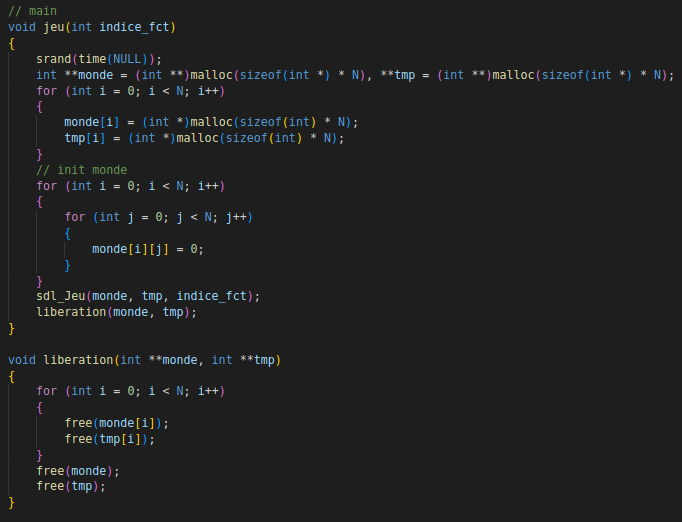
Fonctions jeu avec allocation et libération

---

Animation de Sprites

---

Principe

Cet exercice avait pour but de apprendre le manipulation de sprite et donc d'images avec SDL2, SDL2_TTF et SDL2_IMAGE, notamment en affichant un fond de fenêtre ou en animant une image de personnage.

Démarche

Ici on explique notre démarche sur l'approche de cet exercice

Explications

Ici on explique notre démarche sur l'approche de cet exercice

Code

Ici on explique notre démarche sur l'approche de cet exercice

Détail par personne

Ici on explique notre démarche sur l'approche de cet exercice

---

Chef d'oeuvre

ATTENTION TRAVAUX !

---

Principe

Nous avons donc décidé de proposer un jeu mettant en scène une voiture et des portions de route qui se ferment et se rouvrent selon une chaine de markov se basant sur l'état précédent de la route. L’objectif du jeu étant de ne rouler que sur les routes ouvertes.

Démarche

Dans le cas de notre jeu, nous avons donc la présence de la chaîne de Markov sur les probabilité de fermeture d’une route en connaissant son état à l’instant précédent.
La route est une grille de 3 unités de large et chaque travaux occupe 1 unité. Cependant afin que le joueur ne puisse que perdre à cause de lui-même, nous avons décidé de n'occuper au maximum que 2 des 3 cases et, si 2 cases obstruées il y a, la prochaine vague sera soit la même soit vide.
Les probabilités des états sont donc rangées dans ce tableau double :

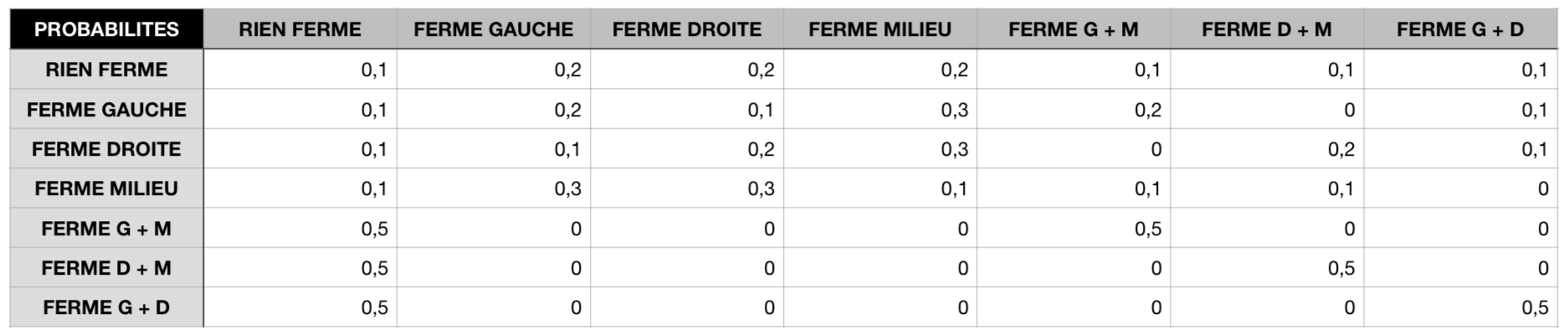
Démarche algorithmique

La chaîne de Markov se base sur tous les états possibles pour les trois routes en même temps. Pour celà, on considère une matrice de 1 (pour l’état fermé) et de 0 (état ouvert) qui permet de déterminer l’aspect de la route sur plusieurs portions. On utilise un entier dans lequel on stocke la ligne de début afin de pouvoir ne remplacer que la dernière ligne (d’un point de vue affichage) par la nouvelle calculée grâce à Markov. Cela évite de devoir modifier toute la matrice à chaque fois.

Pour obtenir ce nouvel état, on demande un nombre entre 1 et 10 puis on détermine à quel état cela correspond. (Les probabilités sont donnée par des entiers entre 1 et 10)

On peut noter ici qu’on pourrait améliorer la lisibilité du programme en associant chaque état (ensemble de 0 et de 1) au nombre binaire associé pour les indices de ligne et de colonne de la matrice de Markov.

Code de l'affichage (SDL2)

Nous avons créé 3 fenêtres :
1. Menu du jeu inspiré du Jeu de la vie avec le bouton JOUER et les Règles.
2. Passage à la fenêtre en cliquant sur jouer puis affichage d’un fond Sprite à 2 images qui s’alternent pour donner une impression de la voiture en mouvement.
Affichage également de la consigne “Appuyez sur ESPACE pour commencer” afin de préparer le joueur à l’exécution de la partie jouable. Le joueur peut d’hors et déjà placer son véhicule sur la voie qu’il souhaite.
Après appuie sur ESPACE les obstacles (travaux) arrivent par ligne (total de 5 lignes) et agissent comme une file lors de leur disparition, FIFO. Ils arrivent grâce aux chaînes de Markov (nouveau comportement influencé par les probabilités sachant le comportement du précédent).
Un compteur est mis en place en haut à droite qui fait +1 à chaque ligne passée.
BUT: esquiver les travaux.
3. Passage à la 3ème fenêtre par collision entre le véhicule et un espace de travaux. Entraîne un affichage du même fond que celui du menu avec notamment le score du joueur.

Potentielles améliorations

- Permettre au mouvements des éléments du jeu d’être plus fluides (gestion du jeu non pas par grille mais selon la position des obstacles)
- Sauvegarder le score maximal et le nom du joueur puis les écraser si celui du nouveau joueur est meilleur. Donc avoir chargé la sauvegarde du score maximal et son joueur au préalable dans le jeu.
- Ajout d'une explosion au niveau de la collision avant passage à la 3ème fenêtre. Ou bien ne pas afficher de 3ème fenêtre et mettre son contenu à la fin de la 2ème au moment de l’explosion de la voiture et donc de la collision.

Code

Traduction état markov

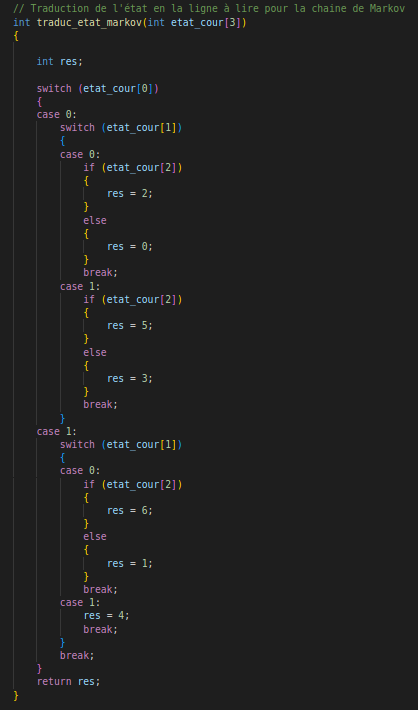
Traduction markov état

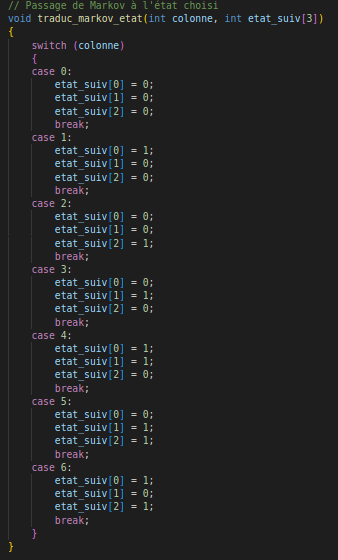
Calcul nouvel état

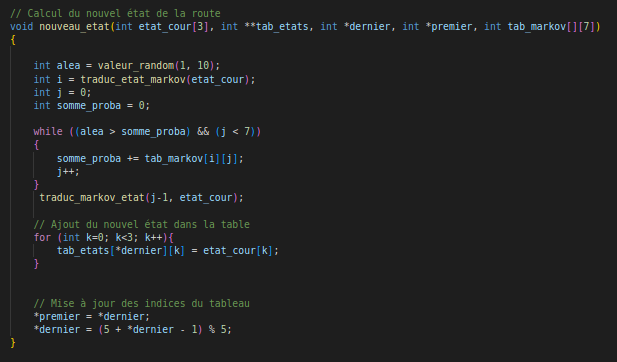
Fonction score

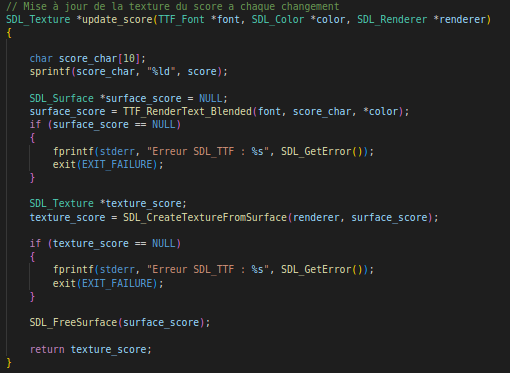
Vidéos

---

Apprentissage par renforcement

⛸ ICE SLIDER ⛸

---

Principe

C'est le projet final que nous avions à réaliser ! Un petit jeu dans lequel une intelligence artificielle joue et apprend via un mécanisme par renforcement.

L'apprentissage par renforcement consiste pour une intelligence artificielle à apprendre les actions à prendre à partir d'expériences et de perceptions, afin d'optimiser les récompenses au cours du temps.
En effet, l'agent intelligent prend une décision en fonction de son état courant et de la perception de son environnement à cet état. En retour, cet environnement lui donne des récompenses, qui peuvent être positives ou négatives.

Au cours de nombreuses tentatives, l'agent va développer un comportement stratégique optimal, qui essaiera de maximiser la somme des récompenses au cours du temps.

Conception

Nous avons décidé pour se faire, de réaliser un jeu sur principe du labyrinthe. Cependant, celui-ci ne sera pas un labyrinthe traditionnel puisque les chemins ne seront pas délimités. Se trouveront seulement sur la zone de jeu, des rochers ou des murs servant de points d'appuis.
En effet le sol sera de glace et le personnage devra, pour atteindre la sortie, bouger dans une des quatres directions de sorte qu'il puisse atteindre un rocher ou un mur et s'appuyer dessus pour aller dans une autre direction. Autrement, il continuera de glisser sur la glace jusqu'à rencontrer un obstacle, même si ce n'est pas le bon chemin.

Le but de l'agent intelligent sera donc d'apprendre à trouver le chemin optimal permettant d'atteindre la sortie. Car oui, plusieurs combinaisons amenent à la même sortie.

Démarche algorithmique

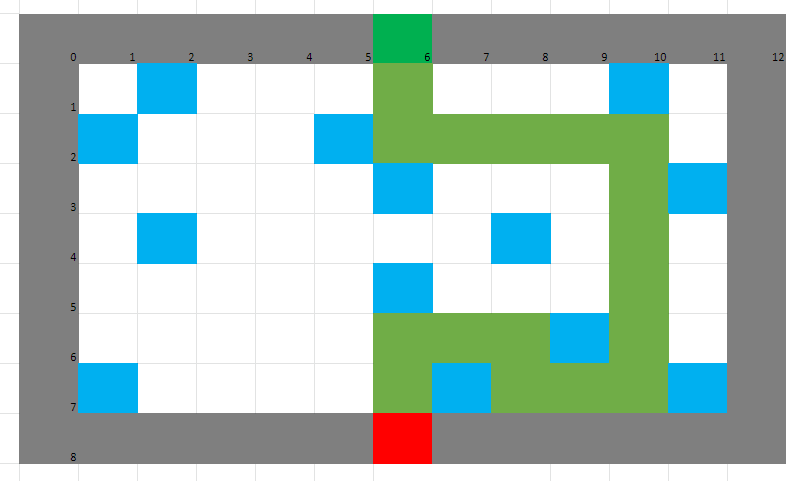
La grille de jeu

Comme vous pouvez le voir sur les images de conception ci-dessus, nous avons décidé de réaliser notre grille de jeu sous ce modèle-ci.
Sur ce schèma sont annotées les coordonnées réelles des cases de la grille dans la fenêtre du jeu mais aussi les indices des cases de la grille dans la matrice algorithmique servant à la gestion des éléments et des collisions avec eux.

- Les murs sont représentés par des cellules grises.
- Les rochers sont représentés par des cellules bleues.
- L'entrée est représentée par une cellule rouge.
- La sortie est représentée par une cellule verte.

Représentés par des cellules beiges sur l'image, nous avons repertorié tous les états possibles dans lequel peut être le joueur en glissant sur la glace et en se réorientant grâce aux obstacles qui sont soit des murs soit des rochers. A ceux-là s'ajoutent l'état de départ ainsi que celui d'arrivée.
Cela nous sera particulièrement utile pour l'apprentissage par renforcement.

Grille de jeu dans le code

Voici à quoi correspondent les chiffres dans la matrice :
- 0 : Cases du labyrinthe sur lequel le personnnage peut aller (glisser dessus ou rester dessus)
- 1 : Murs ou rochers (impossible de se déplacer dessus)
- 2 : Sortie du labyrinthe (objectif à atteindre)

Déplacement du personnage

Le déplacement graphique du personnage est dissocié de la partie matricielle. Pour une expérience plus fluide et plus agréable, on a choisi de gérer le déplacement entre deux cases dans une boucle; entre l'ancienne et la nouvelle calculée.
D'un point de vue plus technique, nous utilisons les coordonées de la texture du personnage dans la fenêtre de jeu pour retrouver les coordonées logiques de cases, grâces à des calculs assez simples.

Exemple de chemin réalisable

Chemin optimal

Collisions avec les murs et les obstacles

Les collisions avec les rochers et les murs sont gérées par le calcul du nouvel état à atteindre.
On détermine la case d'arrivée comme étant la dernière case avant l'obstacle (qu'il soit un mur ou un rocher).
Cela se fait grâce à cette fonction de recherche de 1 dans la matrice de jeu en fonction de la direction choisie :

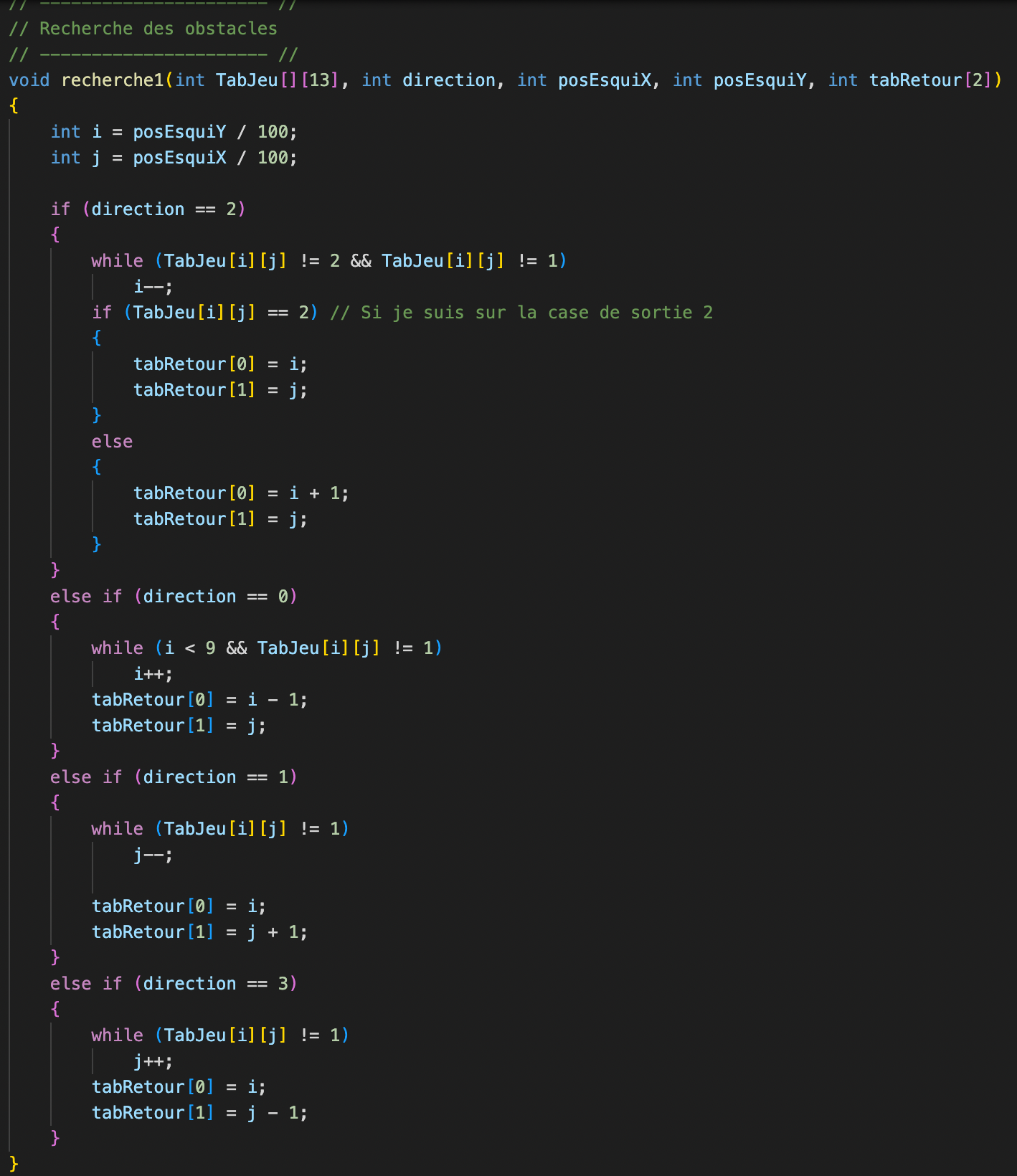
Apprentissage du joueur par renforcement

Choix de l'algorithme

Dans le cadre de notre jeu, reposant sur un labyrinthe, nous voulions que l'intelligence artificielle commence par explorer le plus possible et au fur et à mesure exploiter les résultats des chemins qu'il a déjà emprunté dans le but de prendre les bonnes décisions.
Nous avons donc choisi pour cela d'utiliser l'algorithme e-greedy.

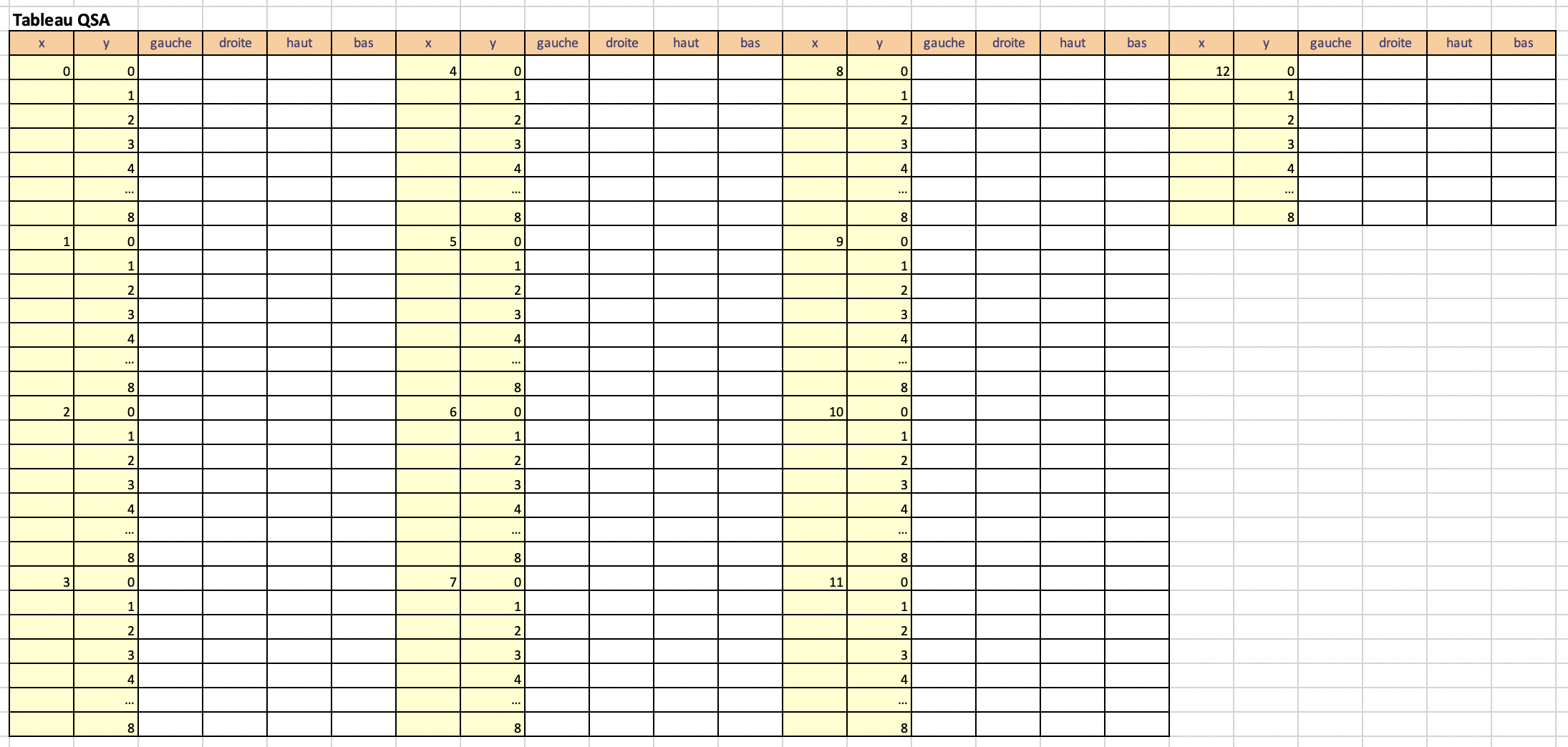
Q Table

Par volonté de simplifier la création de la table QSA, celle-ci contient les coordonnées de toutes les cases du plateau de jeu et, pour chaque couple, nous avons 4 autres cases supplémentaires nous permettant de stocker la valeur des actions possibles, qui sont en réalité les 4 directions: haut, gauche, bas et droite.

Représentation réelle de la matrice QSA

Création de la tablea QSA

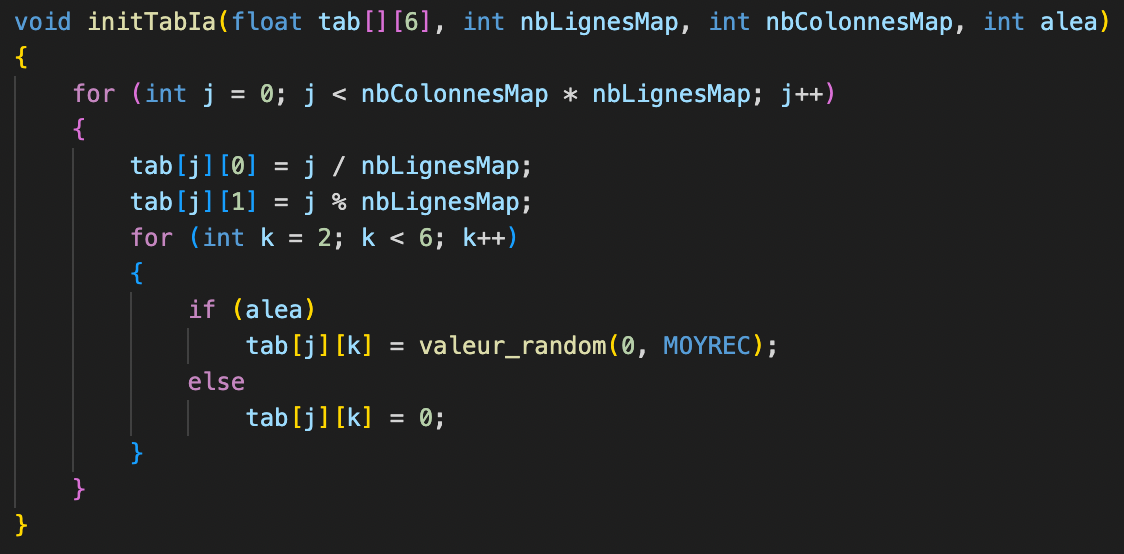
Concernant la création algorithmique de cette table, nous avons créé la fonction ci-dessus.
En utilisant la division euclidienne de notre indice de ligne divisé par le nombre de lignes de la grille de jeu, nous sommes capables de remplir la colonne des x par le nombre possibles de couples de coordonnées pour chaque valeur de x.
Pour cette fois-ci remplir la colonne des y, nous avons replacé la division par le modulo, ce qui nous donne toutes les valeurs de y possibles.

Enfin, pour les cases des actions, nous avons laissé le choix à l'utilisateur entre les initialiser avec des 0 ou alors les initialiser avec des valeurs aléatoires entre 0 et une moyenne de récompenses définie.

Récompenses

Dans notre modèle de jeu, l'environnement renvoie des recompenses à l'intelligence artificielle avec un principe très simple :
Le personnage obtient une récompense de 1 seulement si il se trouve sur la case d'arrivée.
Dans tous les autres cas et donc tous les autres états possibles, il obtient une récompense de 0.
Du point de vue algorithmique, on effectue simplement une vérification des coordonnées du joueur.

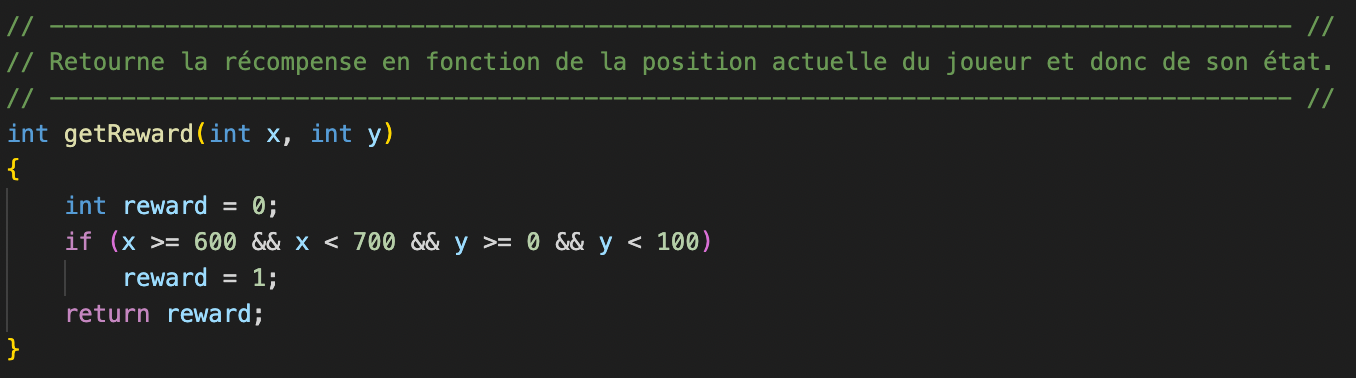
Comment jouer ?

1. Vous êtes au menu, choisissez entre les deux modes :
- Mode manuel : "JOUER"
- Mode automatique : apprentissage par renforcement
2. Si vous avez choisi le mode manuel alors déplacez le personnage avec les flèches directionnelles.
3. En revanche si vous avez choisi le mode automatique, laissez l'intelligence artificielle apprendre et regardez là !
4. Dans les deux modes, dès que vous avez trouvé le sortie, un message apparait, vous pouvez fermer la fenêtre en appuyant sur la croix.

Aperçu

Jeu en manuel depuis le menu

Jeu en apprentissage par renforcement depuis le menu

On voit bien que au bout d'un certain nombre d'époques, il prend désormais le chemin optimal pour rejoindre la sortie.

Complexification du jeu

Dans les derniers instants du développement, nous avons décidé de complexifier l'apprentissage de notre intelligence artificielle.
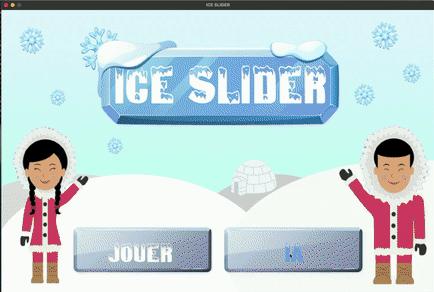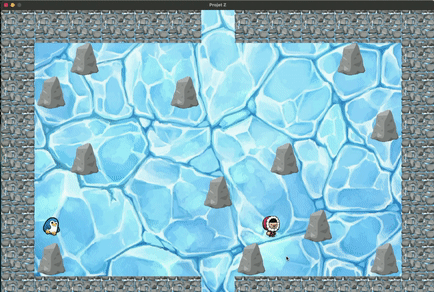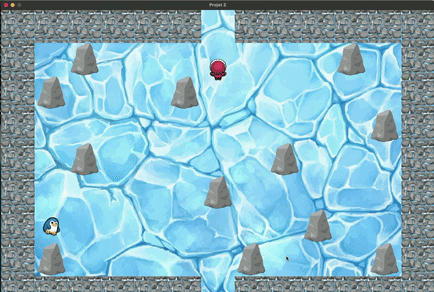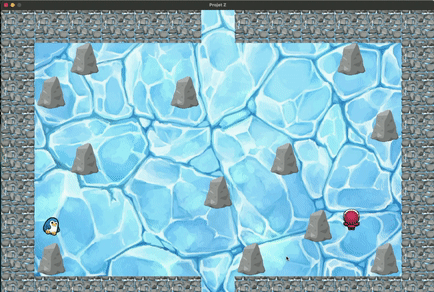
Pour cela nous avons rajouté au jeu un pinguin, que le joueur doit obligatoirement aller chercher avant de trouver la sortie, sinon celle-ci sera bloquée.
(Toute ressemblance du pinguin avec un autre pinguin connu est bien entendu fortuite.)

Pour le mode manuel, le pinguin suit bien le joueur dès que celui-ci vient sur la même case et ce jusqu'à la sortie.

En revanche concernant le mode apprentissage, nous avons encore du mal à le faire fonctionner parfaitement.
En enlevant certains rochers et en plaçant le penguin à un autre endroit, nous arrivons à obtenir un résultat convenable mais pas sur la durée.
Nous cherchons encore une solution et nous travaillerons dessus encore aujourd'hui.

Exemple de fonctionnement correct mais avec concessions

Exemple de fonctionnement incorrect (cyclage)

Améliorations possibles

- Ajouter de nouvelles grilles de jeu.
- Bouton permettant de revenir au menu une fois le jeu terminé.
- Ajouter une bande son au jeu.
- Faire briller le sol en glace.

---