Le triangle de Pascal tire son nom du mathématicien français Blaise Pascal qui l’a étudié au XVe siècle afin d’analyser les combisaisons dans un jeu de hasard. Il montrera par ailleurs plusieurs propriétés sur ce triangle dans le Traité du triangle arithmétique.
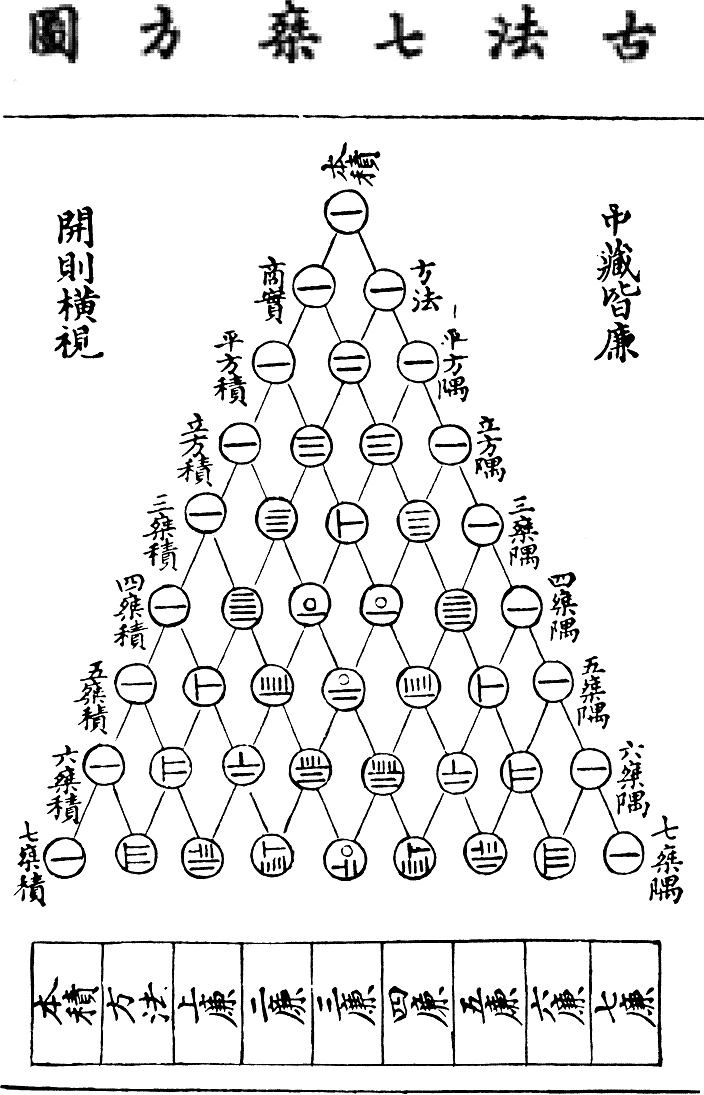
Pourtant, il n’est pas le premier à étudier ce triangle. En effet, plusieurs mathématiens ont déjà étudié ce triangle. On peut, par exemple, le Persan Omar Khayyam au XIe siècle ou le Chinois Zhu Shijie. L’objectif était de développer les expressions mathématiques de la forme \((a+b)^n\).

Le triangle de Pascal s’obtient grâce aux propriétés des coefficients binomiaux.
Pour commencer, nous allons définir la factorielle d’un nombre \(n \in \mathbb{N}^*\). Il s’agit du nombre noté \(n!\) qui est égal au produit de tous les entiers naturels compris entre 1 et n. Autrement dit, on a : \[n! = \prod_{i=1}^n i\]
Ensuite, nous pouvons définir les coefficients binomiaux. Soient \(n\) et \(k\), deux entiers tels que \(0 \leq k \leq n\). On définit le coefficient binomial de “k parmi n” : \[\binom{n}{k} = \frac{n!}{k!(n-k)!}\]
Ce nombre correspond au nombre de combinaisons de \(k\) élements parmi \(n\).
Ce programme en C permet de calculer un coefficient binomial :
#include <stdio.h>
int factorielle (int n) {
int resultat = 1;
int i;
for (i=1; i<=n; i++) {
resultat = resultat * i;
}
return resultat;
}
int coeff_binom(int n, int k) {
return factorielle(n) / (factorielle(k) * factorielle(n-k));
}
int main () {
int n = 5;
int k = 2;
int facto = factorielle(n);
printf("%d\n", facto); // Cela renvoie 120.
int coeff_bin = coeff_binom(n,k);
printf("%d\n", coeff_bin); // Cela renvoie 10.
return 0;
}Les coefficients binomiaux ont plusieurs propriétés :
\(\binom{n}{0} = \binom{n}{n} = 1\)
\(\binom{n}{1} = n\)
\(\binom{n}{k} = \binom{n}{n-k}\)
Mais celle qui nous intéresse le plus est la suivante : \[\binom{n}{k} + \binom{n}{n+1} = \binom{n+1}{k+1}\]
Cette propriété est fondamentale pour construire le triangle de Pascal.
On se place dans un tableau comportant \(n\) lignes et \(k\) colonnes. On note \(i\) et \(j\) les indices respectivement des lignes et des colonnes tels que \(0 \leq j \leq i\).
Chaque case de coordonnées (i,j) correspondra au coefficient binomial \(\binom{i}{j}\).
Voici les différentes étapes de construction : 1. On place 1 dans la case (0,0). 2. Chaque case sur la colonne 0, donc de coordonnées (a,0), prend la valeur 1. 3. Chaque case sur la diagonale, donc de coordonnées (a,a), prend la valeur 1. 4. En additionnant deux coefficients adjacents d’une ligne, on obtient celui situé en dessous du coefficient de droite.
Voici ci-dessous un extrait du triangle de Pascal de taille 7 par 7 :
| n / k | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||
| 1 | 1 | 1 | |||||
| 2 | 1 | 2 | 1 | ||||
| 3 | 1 | 3 | 3 | 1 | |||
| 4 | 1 | 4 | 6 | 4 | 1 | ||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 |
Ce programme en Python permet d’obtenir un triangle de Pascal :
def triangle_pascal(n):
# Création du triangle
t = []
for i in range(n):
ligne = []
for j in range(i+1):
ligne.append(0)
t.append(ligne)
# Remplissage avec les valeurs
for i in range(n):
for j in range(i+1):
if j == 0 or i == j: # Si on est sur la colonne 0 ou sur la diagonale
t[i][j] = 1
else:
t[i][j] = t[i-1][j-1] + t[i-1][j] # Formule de Pascal
print(t[i][j], end="\t")
print("")
print(t)On peut observer plusieurs propriétés avec le triangle de Pascal. En voici quelques unes :
La somme des nombres d’une ligne n est égale à \(2^n\). Par exemple, pour la ligne 4, on a : \(1 + 4 + 6 + 4 + 1 = 16 = 2^4\)
Les sommes des termes des “diagonales ascendantes” forment la suite de Fibonacci : \(1, 1, 2, 3, 5, 8, 13, 21...\) (voir image ci-dessous).
Si on colorie les cases du tableau contenant des valeurs impaires, on obtient une figure similaire au triangle de Sierpinski.
Pour plus d’informations, consulter la page Wikipédia sur le sujet en cliquant ici.
Pour voir la version HTML du document, cliquer ici.
La commande pandoc utilisée pour générer le document HTML est : pandoc -o pascal.html pascal.md -s --mathjax="https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML" --metadata title="Le triangle de Pascal"