Suguru Solver

Page web ISIMA
Fichier .org source
Défi de programmation - Suguru Solver

1. Introduction

Le but de ce problème est de résoudre une variante du sudoku.
Dans cette variante, on se place dans une grille de taille donnée, avec des cages données.
Chaque cage contient chaque chiffre de 1 jusqu’à la taille de la cage.
De plus, les cellules adjacentes, même en diagonale ne peuvent contenir le même chiffre.

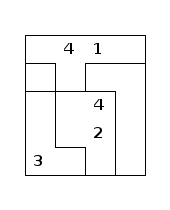
Exemple de suguru :

2. Approche utilisée

Je présente ici ma tentative, mais cette dernière n’a pas aboutit.

2.1. Description synoptique

Le principe de mon algorithme est de tester les cases une par une, si il y a déjà un chiffre on peut passer à la suivante, mais si la case est vide (si elle contient un 0), on test chaque chiffres de 1 à n (où n est le nombre de cellules dans la cage actuelle) si il est possible sur cette case (si le même chiffre n’est pas présent dans les cases adjacentes). Ensuite on passe à la case suivante.

2.2. Algorithme

3. Resolution

#include <stdio.h>
#define M 400

typedef struct ELEM_T {
    int value;
    int cage;
} elem;

void display(elem grid[M], int w, int h) {
    for (int y=0; y<h; ++y) {
        for (int x=0; x<w; ++x) {
            printf("%d", grid[w*y+x].value);
        }
        printf("\n");
    }
}

int isValidPosition(int x, int y, int w, int h) {
    return x >= 0 && x < w && y >= 0 && y < h;
}

// Vérifie si k n'est pas déjà préset dans les cases adjacentes
int possibleNum(elem grid[M], int k, int w, int h, int pos) {
    int x = pos % w;
    int y = pos / w;
    int offsets[][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1},
                        {-1, 1}, {-1, -1}, {1, 1}, {1, -1}};

    for (int i = 0; i < 8; i++) {
        int newX = x + offsets[i][0];
        int newY = y + offsets[i][1];

        if (isValidPosition(newX, newY, w, h)) {
            int newPos = newY * w + newX;
            if (grid[newPos].value == k)
                return 0;
        }
    }
    return 1;
}

int possibleCage(elem grid[M], elem *k, int w, int h) {
    int count = 0;
    for (int i=0; i<w*h; ++i) {
        count += grid[i].cage == k->cage && grid[i].value == k->value;
    }
    return count <= 1;
}

int sizeOfCage(elem grid[400], char c, int w, int h) {
    int count = 0;
    for (int i=0; i<w*h; ++i) {
        count += grid[i].cage == c;
    }
    return count;
}

int possible(elem grid[M], int pos, elem *k, int w, int h) {
    return possibleNum(grid, k->value, w, h, pos) && possibleCage(grid, k, w, h);
}

int solve(elem grid[400], int pos, int w, int h) {
    if (pos >= w*h)
        return 1;

    if (grid[pos].value != 0)
        return solve(grid, pos+1, w, h);

    int num = sizeOfCage(grid, grid[pos].cage, w, h);

    for (int k=1; k <= num; k++) {
        if (possible(grid, pos, &grid[pos], w, h)) {
            grid[pos].value = k;

            if (solve(grid, pos, w, h))
                return 1;
        }
    }
    grid[pos].value = 0;
    return 0;
}

int main() {
    int w;
    int h;
    elem grid[M]; // La grille est stockée dans un tableau 1D

    scanf("%d%d", &w, &h); fgetc(stdin);
    for (int i = 0; i < h; i++) {
        char line[60];
        scanf("%[^\n]", line); fgetc(stdin);

        for (int j=0; j<w; ++j) {
            char numChar = line[3*j + 1];
            int value = (numChar == '.') ? 0 : numChar-'0';
            grid[w * i + j] = (elem) {value, line[3 * j]};
        }
    }

    solve(grid, 0, w, h);
    display(grid, w, h);

    return 0;
}

4. Bilan

J’ai trouvé cet exercice plus compliqué à résoudre que les autres sudoku, ma solution n’a pas aboutit.