Sudoku Solver

Page web ISIMA
Fichier .org source
Défi de programmation - Sudoku Solver

1. Introduction

Le but de ce problème est de simplement résoudre un sudoku.
Un sudoku est une grille de 9x9, divisée en grille de 3x3. Chaque case doit être remplie avec un numéro entre 1 et 9, chaque numéro doit être présent une unique fois sur sa ligne, colonne et sous-grille.
Dans cet exercice, une case vide est représentée par un 0.

Exemple de sudoku :

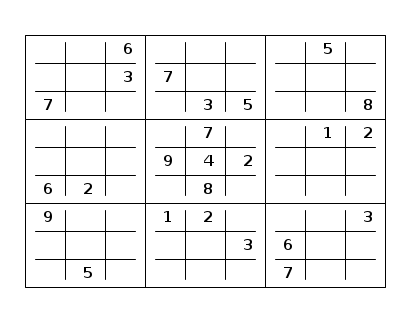
2. Approche utilisée

2.1. Description synoptique

Le principe de mon algorithme est de tester les cases une par une, si il y a déjà un chiffre on peut passer à la suivante, mais si la case est vide (si elle contient un 0), on test chaque chiffres de 1 à 9 si il est possible sur cette case (si il n’est ni présent de la ligne, colonne, ou sous-grille). Ensuite on passe à la case suivante.

2.2. Algorithme

Fonction isValid :
Prend en entrée une grille et une position.
Si position = 9*9:

Renvoyer 1

Si la case d’indice position de la grille différente de 0:

Renvoyer isValid(grille, position+1)

Boucle sur k de 1 à 9 (inclus) :

Si k n’est ni sur la ligne, colonne et sous-grille de la case =position=m
- Case d’indice position = k
- Si isValid(grille, position+1):
  - Renvoyer 1

Case d’indice position = 0
Renvoyer 0

Programme principal :
grille = entrée utilisateur
isValid(grille, 0)
afficher grille

3. Resolution

3.1. Programme

#include <stdio.h>

void display(int grille[9][9]) {
    for (int i=0; i<9; ++i) {
        for (int j=0; j<9; ++j) {
            printf("%d", grille[i][j]);
        }
        printf("\n");
    }
}

int missingOnLine(int k, int grille[9][9], int i) {
    for (int j=0; j < 9; j++)
        if (grille[i][j] == k)
            return 0;
    return 1;
}

int missingOnCol(int k, int grille[9][9], int j) {
    for (int i=0; i < 9; i++)
        if (grille[i][j] == k)
            return 0;
    return 1;
}

int missingOnBlock(int k, int grille[9][9], int i, int j) {
    int i2 = i-(i%3), j2 = j-(j%3);
    for (i=i2; i < i2+3; i++)
        for (j=j2; j < j2+3; j++)
            if (grille[i][j] == k)
                return 0;
    return 1;
}

int isValid(int grille[9][9], int position) {
    // Si on a parcouru tout le sudoku, on sort de la fonction
    if (position == 9*9)
        return 1;

    int i = position/9, j = position%9;

    if (grille[i][j] != 0)
        return isValid(grille, position+1);

    for (int k=1; k <= 9; k++) {
        if (missingOnLine(k,grille,i) && missingOnCol(k,grille,j) && missingOnBlock(k,grille,i,j)) {
            grille[i][j] = k;

            if (isValid(grille, position+1))
                return 1;
        }
    }
    grille[i][j] = 0;
    return 0;
}

int main() {
    int grille[9][9];

    for (int i = 0; i < 9; i++) {
        char line[10];
        scanf("%[^\n]", line); fgetc(stdin);

        for (int j=0; j<9; ++j) {
            grille[i][j] = line[j] - '0';
        }
    }
    isValid(grille, 0);
    display(grille);

    return 0;
}

3.2. Test

A partir de la grille incomplète suivante (sudoku.txt) :

Le programme complète la grille et l’affiche :

4. Comparaison avec une autre solution

A partir de cette solution externe :

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <stdbool.h>

#define N (3)   // Square root of the edge length

char board  [ N*N ][ N*N+1 ];
char board_t[ N*N ][ N*N+1 ]; // Transposed board

bool good( int x, int y, char n );  // Test if number fits
bool solve();

int main()
{
    for (int y = 0; y < N*N; y++) {
        fgets(board[y], N*N+1, stdin);
        fgetc(stdin);
        board[y][N*N] = board_t[y][N*N] = 0;
        for(int x = 0; x < N*N; x++)
            board_t[x][y] = board[y][x];
    }
    solve();
    for (int i = 0; i < N*N; i++ )
        puts( board[i] );

    return 0;
}

bool good( int x, int y, char n ) {
    int xs = x / N * N;
    int ys = y / N * N;
    for( int i = 0; i < N; i++ )
        for( int j = 0; j < N; j++ )
            if( board[ys+i][xs+j] == n )
                return false;
    if( strchr( board[y], n ) || strchr( board_t[x], n ) )
        return false;
    return true;
}

bool solve() {
    for( int y = 0; y < N*N; y++ ) {
        for( int x = 0; x < N*N; x++ ) {
            if( board[y][x] > '0' )
                continue;
            for( char n = '1'; n <= '9'; n++ ) {
                if( good( x, y, n ) ) {
                    board[y][x] = board_t[x][y] = n;
                    if( solve() )
                        return true;
                    board[y][x] = board_t[x][y] = '0';
                }
            }
            return false;
        }
    }
    return true;
}

Cette solution utilise une approche de brute forcing, elle propose de parcourir une par une chaque case du sudoku, et de tester pour chaque case, chaque nombre de 1 à 9, et recommence jusqu’à avoir trouvé une grille correcte.

5. Bilan

Le problème du sudoku est un problème que j’avais déjà résolu dans le passé (en python), il a été plutôt simple à reproduire en C.