Minimax exercise

Page web ISIMA
Documentation
Fichier .org source
Défi de programmation - Minimax exercise

1. Introduction

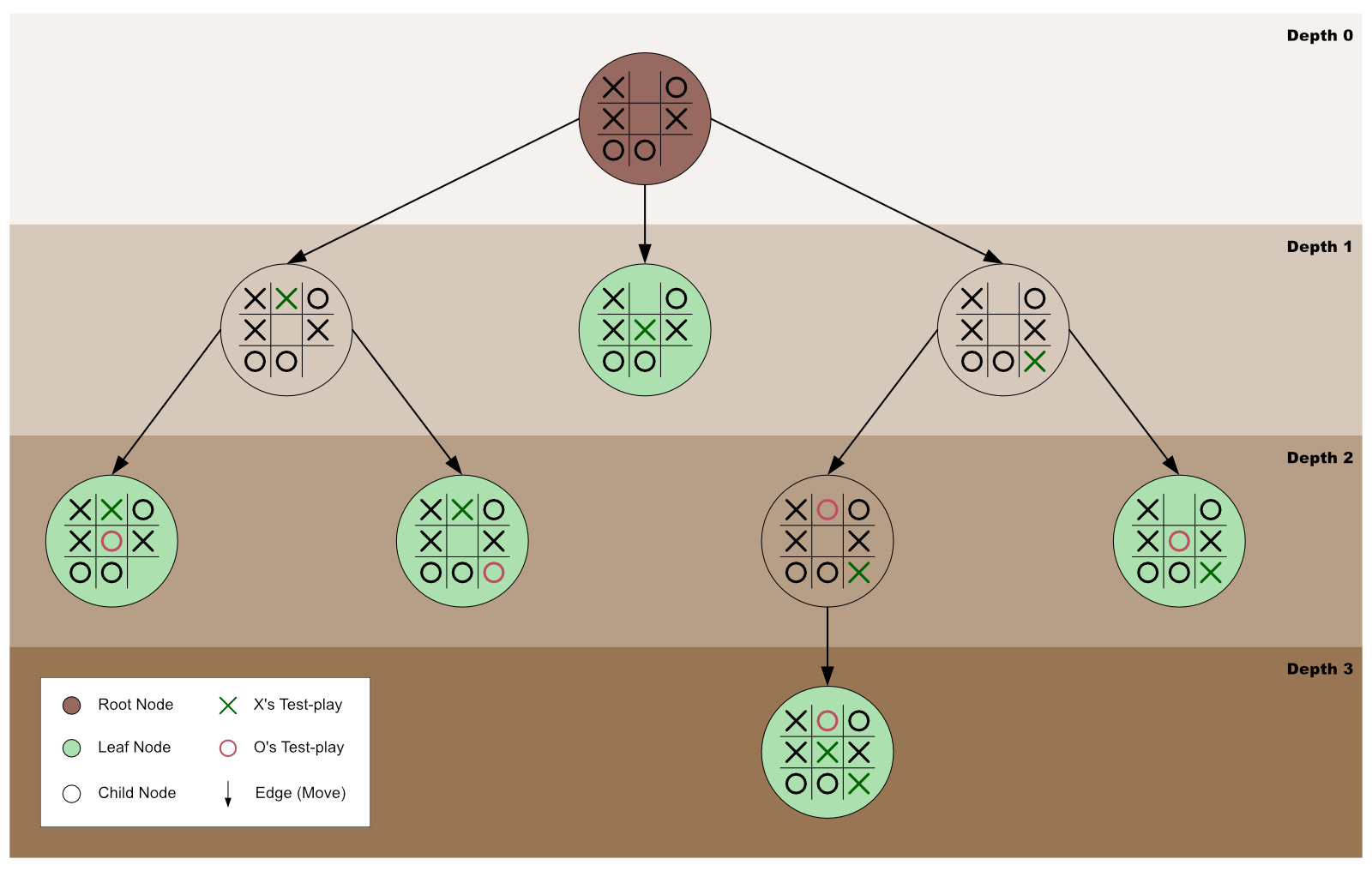
A partir d’un arbre de jeu donné, dans lequel on nous donne les résultats possibles, le but de l’exercice est de calculer le gain minimum pour le 1er joueur, en utilisant un algorithme de Minimax.

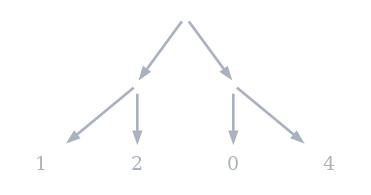
Exemple de partie représentée par un arbre :

2. Approche utilisée

2.1. Description synoptique

Pour résoudre ce problème, j’ai simplement utilisé un algorithme de minimax. A partir de l’arbre donné on choisi une fois sur deux le minimum des scores possible ou le maximum.

Sachant que l’exercice nous donne uniquement les résultats possible et non l’arbre, j’ai pu en déduire qu’en fonction de la partie : elle dure D tours et le joueur peux choisir entre B choix, avec les résultats possible donnés dans l’ordre, au tour numéro n, on a B choix qui se situent tout les B^(D-n) + position choix, dans la liste des résultats.

Pour cet example (D=2) :

Au 1^er tour on a B=2 solutions, qui se situent tout les B^(D-1) = 2¹ = 2 choix, donc aux indices 0 et 2.
Au 2^e tour, pour la 1ère branche, les résultats se situent tout les B^(D-2) = 2⁰ = 1 choix, donc aux indices 0 et 1, pour la 2e branche aux indices 2 et 3.

Sachant désormais comment résupérer les valeurs des feuilles, on applique la logique de minimax et on prend une fois sur 2 le maximum ou le minimum.

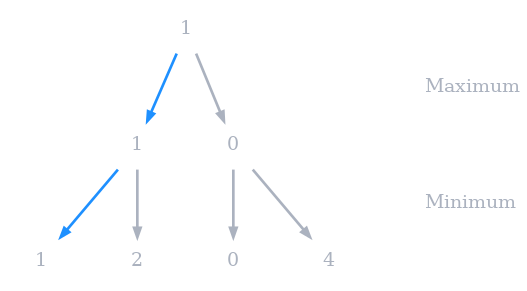
2.2. Algorithme

Fonction minimax :
Prend en entrée une depth, un booléen maxPlayer si on doit maximiser le joueur ou non, alpha et beta des variables d’optimisation, pos la position actuelle dans l’arbre, leafs les feuilles de l’arbre, visitedNodes le compteur de noeuds visités.
Incrémenter visitedNodes
Si depth = 0 :

renvoyer la pos^ième valeur de leafs

stepSize = B^depth-1
Si maxPlayer :

maxEval = -9999
Boucle sur i de 0 à B-1 :
- eval = minimax(depth-1, 0, …, pos + i * stepSize)
- maxEval = max(eval, maxEval)
- alpha = max(alpha, maxEval)
- Si beta <= alpha:
  - Fin boucle
Renvoyer maxEval

Sinon :

minEval = 9999
Boucle sur i de 0 à B-1 :
- eval = minimax(depth-1, 1, …, pos + i * stepSize)
- minEval = min(eval, minEval)
- beta = min(beta, minEval)
- Si beta <= alpha :
  - Fin boucle
Renvoyer minEval

Fonction principale :
D, B, LEAFS : paramètres donnés par l’exercice
visitedNodes = 0
bestScore = minimax(D, 1, -9999, 9999, B, 0, LEAFS, visitedNodes)
Afficher bestScore et visitedNodes

3. Resolution

3.1. Programme

/**
 * @file minimax.c
 * @brief Résolution de Minimax Exercice
 * @author Rémi SCHIRRA
 * @version 1.0
 * @date 7 avril 2024
 */
#include <stdio.h>
#include <stdlib.h>
#define MAX(x, y) (((x) > (y)) ? (x) : (y))
#define MIN(x, y) (((x) < (y)) ? (x) : (y))

/**
 * @brief fonction puissance
 * @param a
 * @param b
 * @return a^b
 */
int power(int a, int b) {
    int result = 1;
    for (int i = 0; i < b; ++i) {
        result *= a;
    }
    return result;
}

/**
 * @brief Trouve la nième valeur présente dans le string donné.
 * @param leafs Le string contenant les valeurs
 * @param index L'emplacement de la valeur à récupérer
 * @return La valeur trouvée, -666 sinon
 */
int leaf(char leafs[], int index) {
    char num[8];
    int j = 0;
    int count = 0;

    for (int i = 0; leafs[i] != '\0'; ++i) {
        if (leafs[i] == ' ' || leafs[i + 1] == '\0') {
            num[j] = '\0';
            j = 0;
            count++;

            if (count == index + 1)
                return atoi(num);
        } else {
            num[j++] = leafs[i];
        }
    }
    return -666;
}

/**
 * @brief La fonction minimax
 * @param depth La profondeur de l'arbre à explorer
 * @param maxPlayer Doit-on maximiser le joueur
 * @param alpha, beta variables d'optimisation
 * @param B Le branching factor donné
 * @param pos La position actuelle dans l'arbre
 * @param leafs Les valeurs tout en bas de l'arbre
 * @param visitedNodes Le compteur de noeuds visités
 */
int minimax(int depth, int maxPlayer, int alpha, int beta, int B,
    int pos, char *leafs, int *visitedNodes) {
    (*visitedNodes)++;

    if (!depth) {
        return leaf(leafs, pos);
    }

    int stepSize = power(B, depth-1);
    int eval;

    if (maxPlayer) {
        int maxEval = -9999;
        for (int i = 0; i < B; ++i) {
            eval = minimax(depth-1, 0, alpha, beta, B, pos+i*stepSize, leafs, visitedNodes);
            maxEval = MAX(eval, maxEval);
            alpha = MAX(alpha, maxEval);
            if (beta <= alpha)
                break;
        }
        return maxEval;
    } else {
        int minEval = 9999;
        for (int i = 0; i < B; ++i) {
            eval = minimax(depth-1, 1, alpha, beta, B, pos+i*stepSize, leafs, visitedNodes);
            minEval = MIN(eval, minEval);
            beta = MIN(beta, minEval);
            if (beta <= alpha)
                break;
        }
        return minEval;
    }
}

/**
 * @brief Programme principal
 * Le programme principal, récupérant les entrées de la profondeur, le branching factor et les feuilles.
 * Détermine le meilleur score et compte le nombre de noeuds de l'arbre visité puis affiche ces valeurs.
 */
int main() {
    int D, B;
    scanf("%d%d", &D, &B);
    fgetc(stdin);
    char LEAFS[40001];
    scanf("%[^\n]", LEAFS);

    int visitedNodes = 0;
    int bestScore = minimax(D, 1, -9999, 9999, B, 0, LEAFS, &visitedNodes);

    printf("%d %d\n", bestScore, visitedNodes);

    return 0;
}

3.2. Test

A partir du test suivant (minimax.txt) :

3 2
-1 0 2 666 -3 -2 666 666

Le programme affiche le score et le nombre de nœuds visités :

0 11

4. Comparaison avec une autre solution

A partir de cette solution externe :

#include <stdlib.h>
#include <stdio.h>
// --------------------------------------------------------------------------
int D,B, visited;
// --------------------------------------------------------------------------
int
eval(void){
    int v;
    scanf("%d",&v);
    return v;
}
// --------------------------------------------------------------------------
void
skip(int depth, int left) {
    int v;
    while (left--) {
        if (depth==0) scanf("%d",&v);
        else          skip(depth-1,B);
    }
}
// --------------------------------------------------------------------------
int
maximize(int depth, int alpha, int beta) {
    visited++;
    if (depth==0) return eval();
    depth--;

    int i = B;
    int maximum = -1000;
    while (i--) {
        int v = minimize( depth, alpha, beta);
        if ( v > maximum) maximum = v;
        if ( v > alpha  ) alpha   = v;
        if ( beta <= alpha ) { // cut-off
            skip(depth, i); // need to skip some input
            break;
        }
    }
    return maximum;
}
// --------------------------------------------------------------------------
int
minimize(int depth, int alpha, int beta) {
    visited++;
    if (depth==0) return eval();
    depth--;

    int i = B;
    int minimum = +1000;
    while (i--) {
        int v = maximize( depth, alpha, beta);
        if ( v < minimum) minimum = v;
        if ( v < beta   ) beta    = v;
        if ( beta <= alpha ) { // cut-off
            skip(depth, i);
            break;
        }
    }
    return minimum;
}
// --------------------------------------------------------------------------
main() {
    scanf("%d%d", &D, &B);
    int m = maximize( D, -1000, +1000);
    printf("%d %d\n", m, visited);
}

Cette solution propose une manière de faire différente : la fonction minimax est séparée en 2 fonctions : maximize et minimize, qui s’appellent l’une l’autre. La gestion des entrées est elle aussi différente, les feuilles ne sont pas stockées dans un tableau au début du programme mais sont récupérée au fur et à mesure.

5. Bilan

Après avoir implémenté l’algorithme de minimax et rencontré quelques problèmes, l’exercice a été tout de même plutôt simple à résoudre.