Killer Sudoku Solver

Page web ISIMA
Fichier .org source
Défi de programmation - Killer Sudoku Solver

1. Introduction

Le but de ce problème est de résoudre une variante du sudoku.
Cette variante hérite des règles de base du sudoku, à savoir qu’un chiffre se trouve une unique fois dans chaque ligne colonne, et sous-grille.
Mais cette variante fournie également des « cages », dans laquelle la somme de ses chiffres doit être égale à un nombre donné (chaque case ne doit pas forcément atteindre toute la même somme).

Exemple de Killer Sudoku :

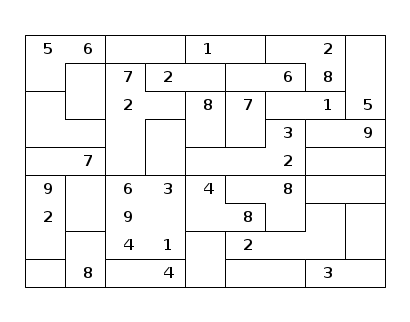
2. Approche utilisée

2.1. Description synoptique

Le principe de mon algorithme est de tester les cases une par une, si il y a déjà un chiffre on peut passer à la suivante, mais si la case est vide (si elle contient un 0), on test chaque chiffres de 1 à 9 si il est possible sur cette case (si il n’est ni présent de la ligne, colonne, ou sous-grille et que la somme dans la cage est correcte). Ensuite on passe à la case suivante.

2.2. Algorithme

3. Resolution

3.1. Programme

#include <stdio.h>
#include <stdlib.h>

void display(int grille[9][9]) {
    for (int i=0; i<9; ++i) {
        for (int j=0; j<9; ++j) {
            printf("%d", grille[j][i]);
        }
        printf("\n");
    }
}

int missingOnLine(int k, int grille[9][9], int i) {
    for (int j=0; j < 9; j++)
        if (grille[i][j] == k)
            return 0;
    return 1;
}

int missingOnCol(int k, int grille[9][9], int j) {
    for (int i=0; i < 9; i++)
        if (grille[i][j] == k)
            return 0;
    return 1;
}

int missingOnBlock(int k, int grille[9][9], int i, int j) {
    int i2 = i-(i%3), j2 = j-(j%3);
    for (i=i2; i < i2+3; i++)
        for (j=j2; j < j2+3; j++)
            if (grille[i][j] == k)
                return 0;
    return 1;
}

int valueOf(char cage[], char cible) {
    int i=0;
    char temp[3];
    while(cage[i]!=cible && i<251){
        ++i;
    }
    ++i;
    temp[0] = cage[i+1];
    temp[1] = cage[i+2];
    int rep = atoi(temp);
    return rep;
}

int possibleCage(int tab[][9],int ligne, int colonne, int entier, char tab_cages[][9], char cages[]){
    char loc = tab_cages[ligne][colonne];
    int valeur_max = valueOf(cages,loc);
    int somme = 0;
    int rec = 0;
    int i,j;
    for(i=0;i<9;++i){
        for(j=0;j<9;++j){
            if(tab_cages[i][j]==loc){
                somme += tab[i][j];
                if (somme+entier > valeur_max) return 0;
                if (tab[i][j] == entier) {
                    return 0;
                }
                if(tab[i][j] == 0){
                    ++rec;
                }
            }
        }
    }
    int test = somme+entier == valeur_max;
    if (rec){
        test = somme+entier <= valeur_max;
    }
    return test;
}

int possible(int grille[9][9], char cages[9][9], char keys[251], int pos, int k) {
    int i = pos/9, j = pos%9;
    int col = missingOnCol(k,grille,j);
    int line = missingOnLine(k,grille,i);
    int block = missingOnBlock(k,grille,i,j);
    int sum = possibleCage(grille, i, j, k, cages, keys);
    return col && line && block && sum;
}

int isValid(int grille[9][9], int position, char cages[9][9], char keys[251]) {
    if (position >= 9*9)
        return 1;

    int i = position/9, j = position%9;

    if (grille[i][j] != 0)
        return isValid(grille, position+1, cages, keys);

    for (int k=1; k < 10; ++k) {
        if (possible(grille, cages, keys, position, k)) {
            grille[i][j] = k;

            if (isValid(grille, position+1, cages, keys))
                return 1;

            grille[i][j] = 0;
        }
    }
    grille[i][j] = 0;
    return 0;
}

int main()
{
    int grille[9][9];
    char cages[9][9];

    for (int i = 0; i < 9; i++) {
        char grid_line[10];
        char grid_cages[10];
        scanf("%s%s", grid_line, grid_cages); fgetc(stdin);

        for (int j=0; j<9; ++j) {
            grille[j][i] = (grid_line[j] == '.') ? 0 : grid_line[j] - '0';
            cages[j][i] = grid_cages[j];
        }
    }
    char keys[251];
    scanf("%[^\n]", keys);

    isValid(grille, 0, cages, keys);
    display(grille);

    return 0;
}

3.2. Test

A partir du test suivant (killerSudoku.txt):

.1..65..7 abcccdeee
6.7....15 fbbgddhie
.54..1..3 fjggdkhil
......... fjmgkknil
16..3.5.. ooppqqnrr
..8..2... sotuvqnnw
3......7. xxtuyyzzA
...3..... BCDDEFzAA
.2.1..349 BBDGGGzzz
a=9 b=16 c=17 d=21 e=18 f=12 g=18 h=15 i=12 j=12 k=15 l=5 m=9 n=19 o=10 p=6 q=12 r=17 s=5 t=13 u=15 v=1 w=4 x=7 y=11 z=33 A=12 B=17 C=9 D=10 E=7 F=4 G=14

Le programme complète la grille en fonction des cages et l’affiche :

4. Bilan

Le problème a été plus dur à résoudre que le sudoku classique, surtout d’un point de vue rapidité de l’algorithme.
Mon algorithme fonctionne mais dépasse le temps maximum sur certains tests de Codingame.