Dwarfs standing on the shoulders of giants

Page web ISIMA
Fichier .org source
Défi de programmation - Dwarfs standing on the shoulders of giants

standing-on-the-shoulders-of-giants-6311c8ce-31e4-427b-b657-5d58abaab21-resize-750.jpeg

1. Introduction

Dans cet exerecice, on nous donne une chaîne de relation, avec une personne qui en influence une autre etc. Le but est de déterminer la longueur de la plus grande chaîne.

Exemple de chaîne de relation :

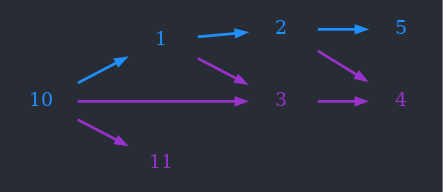
La chaîne la plus longue est la bleu, de longueur 4.

2. Approche utilisée

2.1. Description synoptique

Mon approche a été de d’abord stocker les relations sous forme de chaîne d’élements individuels, chaque éléments possède une valeur et les valeurs des éléments qu’il influence.
Il suffit ensuite de parcourir chaque chaîne et en garder la plus longue.

2.2. Algorithme

maillon : structure contenant :

current : la valeur du maillon
nexts : la liste des maillons engendrés
size le nombre d’éléments dans nexts

elems : liste de maillon

Fonction len :
Renvoie la taille de la plus grande chaîne à partir du paramètre e (un maillon) donné.
Si e->size = 0:

Renvoyer 1

max = 0
Pour chaque éléments k de e->nexts:

max = maximum entre max et len(k)

Renvoyer max + 1

Fonction explore :
Renvoie le maximum de longueur de toutes les chaînes.
max = 0
Pour chaque maillon k de elems:

max = maximum entre max et len(k)

Renvoyer max

Programme principal :
Pour chaque relations x –> y entrées par l’utilisateur:

Ajouter la relation à elems

Afficher explore(elems)

3. Resolution

3.1. Programme

#include <stdlib.h>
#include <stdio.h>
#define MAX(a,b) (((a)>(b))?(a):(b))

typedef struct maillon_T {
    int current;
    struct maillon_T **nexts;
    int size;
} maillon;

maillon *newMaillon(int x) {
    maillon *new = malloc(sizeof(maillon));
    new->nexts = 0;
    new->current = x;
    new->size = 0;
    return new;
}

maillon *findMaillon(maillon **elems, int *n, int x) {
    for (int i=0; i<*n; ++i) {
        maillon *e = elems[i];
        if (e->current == x) {
            return e;
        }
    }
    *n+=1;
    maillon *new = newMaillon(x);
    elems[*n-1] = new;
    return new;
}

void add(maillon **elems, int *n, int x, int y) {
    maillon *a = findMaillon(elems, n, x);
    maillon *b = findMaillon(elems, n, y);
    a->nexts = realloc(a->nexts, sizeof a->size+1);
    a->nexts[a->size] = b;
    a->size++;
}

int len(maillon *e) {
    if (e->size == 0) return 1;
    int max = 0;
    int i;
    for (i=0; i<e->size; ++i) {
        max = MAX(max, len(e->nexts[i]));
    }
    return 1+max;
}

int explore(maillon **elems, int n) {
    int max = 0;
    int i;
    for (i=0; i<n; ++i) {
        max = MAX(max, len(elems[i]));
    }
    return max;
}

int main()
{
    int n;
    maillon **elems;
    int num = 0;

    scanf("%d", &n);
    elems = malloc((n+1) * sizeof elems);

    for (int i = 0; i < n; i++) {
        int x;
        int y;
        scanf("%d%d", &x, &y);

        add(elems, &num, x, y);
    }

    printf("%d\n", explore(elems, num));
    return 0;
}

3.2. Test

A partir du test suivant (dwarf.txt) :

Le programme reconstitue l’arbre correspondant :

En détermine la longueur de la plus grande chaîne et l’affiche :

4. Comparaison avec une autre solution

A partir de cette solution externe :

#include <stdlib.h>
#include <stdio.h>
#include <string.h>

// -------------------------------------------------------------------------
typedef struct {
    int person;
    int next;
} list;

int persons[10000];
int depth[10000];
int freeIndex = 1;
list L[10000];
// -------------------------------------------------------------------------
int max(int a, int b) { return a>b?a:b; }
// -------------------------------------------------------------------------
int deep(int x) {
    if (depth[x] == 0) {
        int maxDepth = 0;
        for (int i = persons[x] ; i ; i = L[i].next)
            maxDepth = max( maxDepth, deep(L[i].person));
        depth[x] = maxDepth+1;
    }
    return depth[x];
}
// -------------------------------------------------------------------------
int main() {
    int N=0; // biggest person number

    int n; // the number of relationships of influence
    scanf("%d", &n);

    for (int i = 0; i < n; i++) {
        int x,y; // a relationship of influence between two people (x influences y)
        scanf("%d%d", &x, &y);

        N = max(N,x);

        // add a relation 'y' to  person 'x'
        int next            = persons[x];
        persons[x]          = freeIndex;
        L[freeIndex].person = y;
        L[freeIndex++].next = next;
    }

    int answer = 0;
    for (int x = 0 ; x <= N ; x++)
        answer = max(answer,deep(x));

    printf("%d\n",answer); // The number of people involved in the longest succession of influences
}

Cette solution propose elle aussi une fonction récursive pour trouver la chaîne la plus grande, mais stocke les données différemment. Le principe reste similaire.

5. Bilan

J’ai compris rapidement comment résoudre le problème et en ai trouvé une solution qui fonctionne. Je suis néanmoins conscient que cette dernière peut être améliorée.