La conjecture de Syracuse

1 Introduction

La conjecture de Syracuse, aussi appelée algorithme ou suite de Syracuse, est un problème mathématique à l’énoncé élémentaire qui défie les chercheurs depuis plus de 80 ans. Cette page est donc consacrée à la présentation de cette conjecture. Mais tout au long de cette présentation on va également se demander si il est possible de démontrer la conjecture de Syracuse.

Dans un premier temps, vous pourrez retrouver une présentation de la conjecture de Syracuse. Puis, vous trouverez une étude simplifiée de certaines propriétés qui pourraient permettre de démontrer cette conjecture, et enfin il vous sera présenté différentes tentatives de démonstration de cette conjecture qui se sont rapprochés de la résolution sans jamais vraiment l’atteindre.

2 Présentation

2.1 Approche historique

Contrairement à ce que l’on pourrait penser, n’a pas été créé par Archimède de Syracuse. En effet elle a été émise en 1937 par un mathématicien allemand Lothar Collatz. Elle porte le nom de Syracuse en référence à une université aux États Unis qui a longtemps essayé de la démontrer. Cette conjecture a fait beaucoup parlé d’elle, elle a fait tellement parler d’elle que durant la guerre froide, une plaisanterie selon laquelle cette conjecture était au coeur d’un complot soviétique, afin de ralentir la recherche américaine courrait dans le milieu de la recherche. Le livre La conjecture des hirondelles s’est d’ailleurs inspiré de cette légende urbaine.

2.2 Présentation de la suite

2.2.1 Définition

Cette conjecture est défini sous la forme d’une suite qui est une liste de nombres reliés par une relation mathématiques. Pour trouver les termes de la suite de Syracuse, c’est à dire les différents éléments de la liste, on choisit un nombre entier différent de 0, si il est pair on le divise par 2, sinon on le multiplie par trois puis on ajoute 1. Ensuite on réitère le processus avec le résultat du calcul précédent.
Après avoir atteint le nombre 1, les valeurs 4, 2, 1 se répète indéfiniment, en un cycle de longueur 3 appelé cycle trivial. A priori, il serait possible que la suite de Syracuse de certaines valeurs de départ n’atteigne jamais la valeur 1, soit qu’elle aboutisse à un cycle différent du cycle trivial, soit qu’elle diverge vers l’infini. Mais, on n’a jamais trouvé d’exemple de suite obtenue suivant les règles données qui n’aboutisse pas à 1 et, par la suite, au cycle trivial.

On peut définir la suite de Syracuse de la manière suivante :

$\left\{\begin{array}{rcl} U_0&=&n \\ U_{n+1}&=&\frac{U_n}{2},~si~U_n~est~pair \\ U_{n+1}&=&U_n\times 3+1,~si~U_n~est~impair \end{array}$

$\forall n\in \mathbb{N}$

2.2.2 Exemple

Prenons l’exemple de la suite de Syracuse pour $U_0=13$:

• $13\times 3+1=40$

• $\frac{40}{2}=20$

• $\frac{20}{2}=10$

• $\frac{10}{2}=5$

• $5\times 3+1=16$

• $\frac{16}{2}=8$

• $\frac{8}{2}=4$

• $\frac{4}{2}=2$

• $\frac{2}{2}=1$

Si l’on traduit ces calculs sous forme de tableau on obtient :

3 Informations notables

3.1 Propriétés particulières

3.1.1 Etude graphique

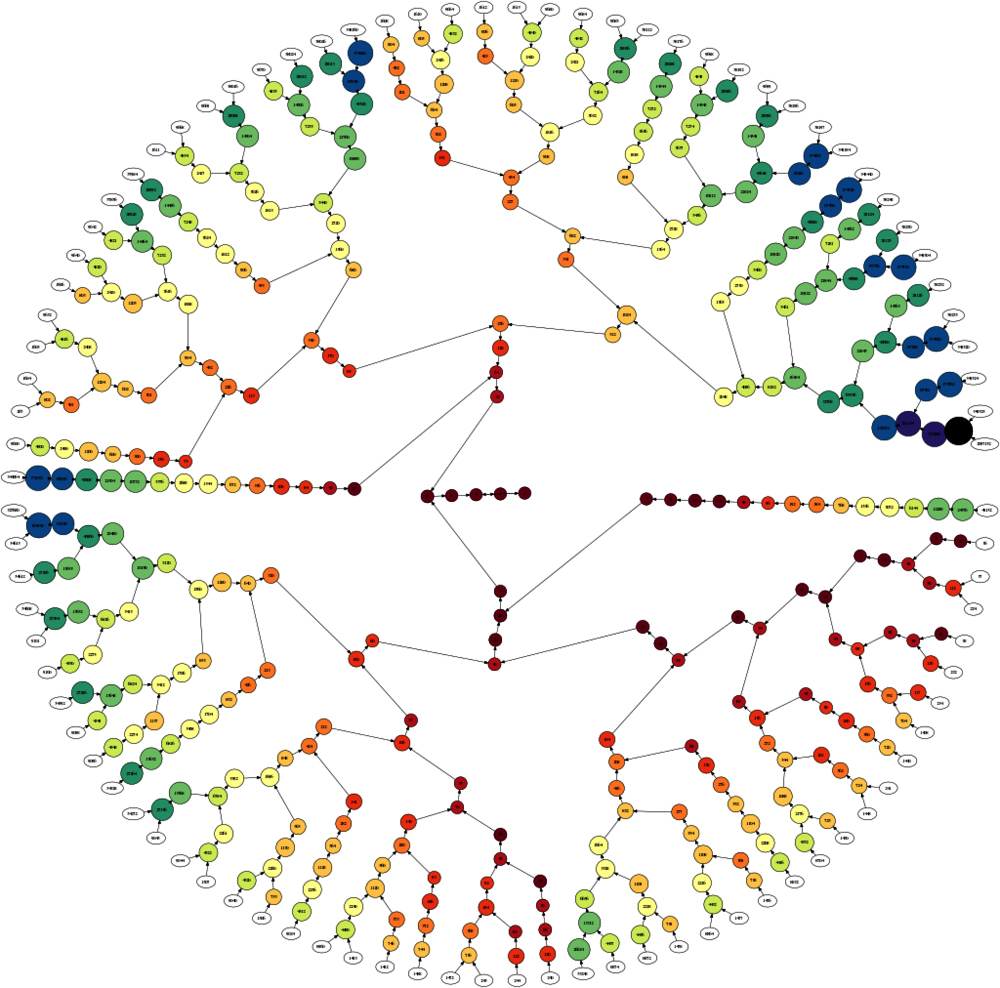
Cette conjecture est intéressante car elle présente certaines propriétés particulières. En effet l’observation graphique de la suite montre qu’elle peut atteindre des valeurs très grandes avant d’atteindre 1. Ces graphiques font penser à la trajectoire d’une feuille emportée par le vent (voir figure 1). De cette observation est né tout un vocabulaire imagé : on parlera du vol de la suite. On définit alors :

• le temps de vol : c’est le nombre de fois où l’on doit appliquer l’algorithme avant de trouver le nombre 1.
  C’est plus petit indice n tel que $U_n=1$

• le temps de vol en altitude : c’est le nombre de fois où l’on doit appliquer l’algorithme pour trouver une valeur inférieure au nombre choisi au départ. C’est le plus petit indice n tel que $U_n+1 < U_0$

• l’altitude maximale : c’est la valeur la plus grande de la suite.

L’étude graphique permet d’aider à la recherche d’un contre exemple à cette conjecture. En effet on s’est rendu compte qu’il n’est pas nécessaire de calculer toutes les valeurs de la suite jusqu’à obtenir 1 pour trouver un contre exemple. Il suffit de calculer les valeurs tant qu’elles ne deviennent pas inférieur au nombre choisi au départ. On peut dès lors éliminer certains nombres lorsque l’on recherche un contre exemple, comme les nombres pairs (on les divisent par deux donc le nombre obtenu est inférieur au nombre de départ), ou les nombres pouvant s’écrire sous la forme 4k+1, comme le nombre 13 ($4\times 3+1$).

3.1.1.1 Démonstration

On applique l’algorithme de Syracuse au nombre $4k+1, k>0$ :

$4k+1$ est un nombre impair, donc on le multipli par 3 et on ajoute 1 :

$(4k+1)\times 3+1=2\times (6k+2)$

$2\times (6k+2)$ est un nombre paire, donc on le divise par 2 :

$\frac{2\times (6k+2)}{2}=6k+2$

$6k+2$ est pair, donc on le divise par 2 :

$\frac{6k+2}{2}=3k+1$

Or $3k+1 < 4k+1$, donc d’après la propriété vu précedemment, on en concu que la suite va forcemment retombre sur 1. Les nombres sous la forme $4k+1$ ne peuvent pas être un contre exemple à la conjecture.

3.1.2 Approche algorithmique

Il est possible de programmer la suite de Syracuse dans différents langages de programmation. Voici alors deux exemples de programmes réalisés dans deux langages différents.

1. Suite de Syracuse programmée avec Python 3 :

def suite_syracuse(n):
    suite = [n]             # Définition et initialisation de la suite
    
    while suite[-1] != 1:           # On execute le programme tant que l'on a pas atteint la valeur 1
        if suite[-1] % 2 == 0:              # Test si le dernier terme de la suite est pair
            suite.append(suite[-1] // 2)        # Si oui, on divise par deux
        else:
            suite.append(suite[-1] * 3 + 1)      # Sinon, on multipli par 3 et on ajoute 1

    return suite              # On retourne la suite de Syracuse obtenue

2. Suite de Syracuse programmée en C:

#include<stdio.h>

int main(){

// Initialisation des variables

  int n;
  int n1;
  n1 = 0;

// Choix de la valeur de départ de la suite par l'utilisateur

  printf("Choisissez un entier");
  scanf("%d",&n);

// Tant que la suite n'a pas atteint la valeur 1

  while(n!=1){

// Si n est pair, alors on le divise par 2

    if(n%2 == 0){
      n1 = n / 2;

// Si n est impair, alors on le multipli par 3 et on ajoute 1

    }else{
      n1 = n*3+1;

// Changement de variable et affichage du terme suivant de la suite

    }n = n1;
     printf("%d\n",n);
}}

4 Tentatives de démonstration

Interessons nous maintenant aux tentatives de démonstration les plus intéressantes liées à cette conjecture.

En septembre 2019, Terence Tao mathématicien de l’Université de Californie à Los Angeles, a démontré que la conjecture est “presque” vraie pour “presque” tous les entiers. C’est l’avancée la plus significative du problème depuis de nombreuses années. Sa démonstration ne conclut pas que l’aboutissement est le nombre 1, mais que la suite passe toujours par un minimum.
Mais Tao a lui même dit qu’il y a peu d’espoir d’utiliser ses méthodes pour trouver une preuve complète. Dans son article, il dit que c’est «bien au-delà des méthodes actuelles».

De plus depuis 2009, Tomás Oliveira e Silva, de l’université d’Aveiro, au Portugal, détient le record de vérification de la conjecture de Syracuse par ordinateur. Il a vérifié qu’effectivement, la trajectoire de tout nombre entier positif inférieur à $1,003\times 10^20$ retombe bel et bien sur 1. Mais, même avec ces connaissances très poussées, personne n’a jamais réussi à démontrer ce résultat, car même des miliers d’exemples vrais ne remplacent pas une preuve.

Alors pour prouver la conjecture il faudrait prouver que :

• la suite tourne en rond dans le cycle trivial 4,2,1

• l’affirmation “pour certaines valeurs de n, $n_k$ ne prend jamais les même valeu, et donc quand k tend vers l’infini, $n_k$ tend vers l’infini” est fausse

• l’affirmation “pour certains n, $n_k$ prend deux fois une même valeur, autre que 4,2, et 1 ce qui aboutirai à un nouveau cycle” est fausse

Se pose alors la question de l’indécidabilité. Cette théorie a été exposée par le mathématicien anglais Jhon Horton Conway. Alors, le problème de Syracuse ne serait ni vrai, ni faux. L’idée serait de trouver un nombre de départ qu’on serait incapable de faire atterrir sur 1. Mais en même temps on ne saurait pas prouver qu’il n’atterrira jamais sur 1, ce qui est assez paradoxal.

5 Conclusion

Cet algorithme a donc mobilisé de nombreux mathématiciens, permis beaucoup d’hypothèse et possède certaines propriétés très particulières. Mais comme de nombreuses pistes ont déjà été exploré, la seule solution de preuve qui semble s’offrir a cet algorithme est l’avancée technique des mathématiques actuelles. On peut alors s’interroger sur l’importance de cet algorithme pour les mathématiques modernes.

NB : Afin de transformer mon code .md en une page en .html, j’ai utilisé la commande suivante :

pandoc suitedesyracuse.md -o suitedesyracuse.html -s -N --mathml_