Rapport sur Suguru Solver
Table of Contents
Présentation du problème
Suguru Solver est un problème du site Codingame. Il consiste en la création d’un programme permettant de résoudre les grilles de jeu de Suguru. Le jeu du Suguru est un problème de type casse-tête et logique, où le but est des remplir une grille de nombre en respectant certains critères. Voici les informations essentielles à connaitre sur ce jeu:
- La grille de Suguru est de dimension variable.
- La grille de Suguru est découpée en cages, ce sont des zones contenant une ou plusieurs cases.
- Chaque case doit être remplie de la façon suivante:
- Les cages doivent contenir les nombres de 1 à la taille de la cage (une cage de 3 cases doit contenir les nombres 1,2 et 3).
- Chaque case ne doit pas contenir la même valeur que ses cases adjacentes (diagonales comprises).
- Il y a une unique solution pour chaque grille.
Afin de pouvoir résoudre ce problème, le site Codingame nous fourni un certain nombre d’entrée. Tout d’abord, le site nous donnes les dimensions de la grille de Suguru donnée en entrée. Puis, le site nous donne ligne par ligne la grille de Suguru sous la forme suivante. Chaque case est composée d’une lettre majuscule, et d’un nombre ou d’un point. Si la case possède un nombre, cela correspond à sa valeur. Si elle possède un point, cela signifit qu’il faut déterminer sa valeur. Les lettres quant à elles représentent les cages, il peut y avoir une même lettre qui représente plusieurs cages, puisque les cases de même cages doivent être adjacentes (diagonales non incluses).
Prenons un exemple:
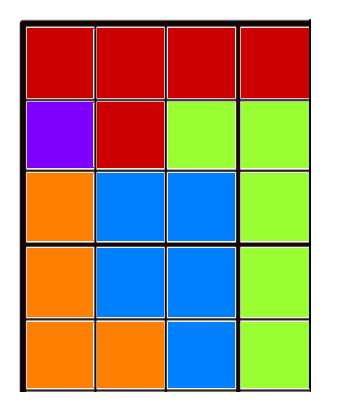
4 5 G. G4 G1 G. R. G. B. B. G. R. R4 B. G. R. R2 B. G3 G. R. B.
Voici un des test proposé par Codingame, les cages représentées seront donc les suivantes:
Métode de résolution
Description de la stratégie
Afin de résoudre ce problème, il me fallait reprendre le principe des anciens puzzle sudoku, et le modifier pour qu’il prenne en compte les spécificitées de ce problème. Ainsi, j’ai pu découper mon code en plusieurs parties afin de pouvoir décrire au mieux ma démarche de résolution.
Partie 1: Instanciation des variables
typedef struct st_case{ // Définition d'une structure représentant une case int valeur; char cage; }st_case; st_case tab[20][20]; // Grille de suguru char cages[20][20]; // Grille avec les cages uniquement st_case occ[100]; int w; int h;
Dans cette première partie, on défini une structure permettant d’avoir à la fois la valeur de la case, et la cage à laquelle elle appartient. Cela permet de concentrer l’information et de pouvoir y accéder plus facilement. On défini également plusieurs variables qui nous seront utiles par la suite.
Partie 2: Fonction test
int test(int i, int j, int n, int occ){ // Fonction qui test la validité du nombre int y=0; int x=0; int count=0; // Test les nombres adjacent à la case que l'on souhaite remplir if((i!=0)&&(j!=0)&&(tab[i-1][j-1].valeur==n)){ // haut-gauche return 0; } if((i!=0)&&(tab[i-1][j].valeur==n)){ // haut return 0; } if((i!=0)&&(j!=w-1)&&(tab[i-1][j+1].valeur==n)){ // haut-droite return 0; } if((j!=0)&&(tab[i][j-1].valeur==n)){ // gauche return 0; } if((j!=w-1)&&(tab[i][j+1].valeur==n)){ // droite return 0; } if((i!=h-1)&&(j!=0)&&(tab[i+1][j-1].valeur==n)){ // bas-gauche return 0; } if((i!=h-1)&&(tab[i+1][j].valeur==n)){ // bas return 0; } if((i!=h-1)&&(j!=w-1)&&(tab[i+1][j+1].valeur==n)){ // bas-droite return 0; } int verif[10]; // Creation d'un tableau rempli de 1 for(int k=0;k<occ;k++){ verif[k]=1; } verif[n-1]=0; // Parcour de la grille while((y<h)&&(occ!=count)){ while((x<w)&&(occ!=count)){ if((tab[i][j].cage==tab[y][x].cage)&&(tab[y][x].valeur!=0)){ // Si le nombre appartient à la même cage que la case traitée et si le nombre n'est pas 0 if(verif[tab[y][x].valeur-1]==1){ // Si le nombre n'est pas déja présent dans la cage verif[tab[y][x].valeur-1]=0; // On l'ajoute à la liste des nombres présents count++; }else{ return -1; } } x++; } x=0; y++; } return 1; }
Cette fonction permet de tester si une case de coordonnées x,y peut prendre la valeur d’un certain nombre. Pour cela, la fonction vérifie si le nombre respecte toutes les propriétées du suguru. On reviendra plus en détail sur cette fonction lors du détail algorithmique.
Partie 3: Fonction getocc
int getocc(int y, int x){ // Permet de connaitre le nombre d'élement de chaque cage int c=0; for(c=0;c<100;c++){ if(tab[y][x].cage==occ[c].cage){ // Si on trouve dans la liste occ le nom de la cage dans laquelle se trouve la case x,y return occ[c].valeur; // On renvoi le nombre d'élement de la cage } } return 0; }
Cette fonction permet de connaitre le nombre d’élement d’une cage. Elle utilise simplement une boucle for qui parcoure un tableau où sont stockées le nombre d’élements de chaque cage.
Partie 4: Fonction solve
void solve() { // Fonction récursive qui permet la résolution de la grille int y, x,n; for (y = 0; y < h; y++) { for (x = 0; x < w; x++) { if (tab[y][x].valeur == 0) { // Si la case que l'on regarde n'est pas remplie int occ=getocc(y,x); // On récupère le nombre d'élement de sa cage for(n = 1; n <= occ ; n++){ // On test tout les nombres possibles if (test(y, x, n, occ)==1){ // Si le test est positif tab[y][x].valeur = n; // On rempli la case avec la valeur solve(); // On rappel la fonction pour finir de compléter la grille tab[y][x].valeur = 0; // Remise à 0 de la case si mauvais choix } } return; } } } // Affichage du résultat for (int i = 0; i < h; i++) { for (int j = 0; j < w; j++) { printf("%d", tab[i][j].valeur); } printf("\n"); } exit(0); }
Dans cette partie, on retrouve la fonction solve, utilisant le mécanisme de récursion, qui va nous permettre de trouver la solution à la grille. Si le nombre que l’on souhaite ajouter respecte les conditions du Suguru, on va ré-appeler la fonction solve pour continuer à compléter la grille. Si ce n’est pas le cas, on va revenir en arrière en testant de remplir la grille avec d’autres nombres.
Partie 5: Fonction voisin
int voisin(int i, int j, char name, int count,int teste[21][21],char new_name,int h,int w){ if ((cages[i][j]!=name)&&(cages[i][j]!=new_name)){ // Si l'élement testé n'appartient pas à la cage return count; } count++; // Ajoute 1 au compteur teste[i][j]=1; // Marque la case comme déja explorée tab[i][j].cage=new_name; // Renome la cage avec un nom unique cages[i][j]=new_name; // Renome la cage avec un nom unique if((i!=0)&&(teste[i-1][j]!=1)){ // Si on est pas sur le bord supérieur de la grille count=voisin(i-1 , j, name, count, teste, new_name,h,w) ; // On test la case du dessus } if((j!=0)&&(teste[i][j-1]!=1)){ // Si on est pas sur le bord gauche de la grille count=voisin(i , j-1, name, count, teste, new_name,h,w) ; // On test la case de gauche } if((j!=w-1)&&(teste[i][j+1]!=1)){ // Si on est pas sur le bord droit de la grille count=voisin(i , j+1, name, count, teste, new_name,h,w) ; // On test la case de droite } if((i!=h-1)&&(teste[i+1][j]!=1)){ // Si on est pas sur le bord inférieur de la grille count=voisin(i+1 , j, name, count, teste, new_name,h,w) ; // On test la case du dessous } return count; }
Dans cette partie, on définit la fonction voisin, qui a pour but de calculer le nombre d’élement de chaque cage. Ainsi, on pourra se servir de cette donnée afin de créer les nouvelles conditions vu au dessus. Cela diminuera donc la complexité de notre code, et donc son temps d’execution. La fonction va regarder les cases adjacentes à la case appelée. Si ces cases font également parti de la même cage, on incrémentera de 1 le compteur, et on rappelera la fonction avec pour coordonnées les cases détectées comme appartenant à la même cage que la case d’origine. Et ainsi de suite. Cela nous permettra d’obtenir toutes les cases d’une cage sans avoir à parcourir toute la grille.
Remarque: On peut retrouver des détails et des schéma sur le fonctionnement de cette fonction dans le rapport killer sudoku solver dans la section Codingame de ma page web.
Partie 6: Récupération des entrées
// Définition de compteurs int j,count,count2; int c=0; int c2=0; scanf("%d%d", &w, &h); fgetc(stdin); // Récupération des dimensions // Récupération des entrées for (int i = 0; i < h; i++) { char line[60]; scanf("%[^\n]", line); fgetc(stdin); j=0; count=0; count2=0; while(line[j]!='\0'){ if((line[j]>='1')&&(line[j]<='9')){ tab[i][count].valeur=line[j]-'0'; tab[i][count].cage='!'; count++; }else if(line[j]=='.'){ tab[i][count].valeur=0; tab[i][count].cage='!'; count++; }else if((line[j]<='Z')&&(line[j]>='A')){ cages[i][count2]=line[j]; count2++; } j++; } }
Dans cette partie se trouvant au début du programme principal, on va définir des compteurs utiles pour la suite, puis on va récupérer les entrées fourni par Codingame. Ces entrées sont données sous la forme d’une chaine de caractère. Alors, on va regarder pour chaque ligne, chaque élement de la ligne. Lorsque l’on trouve une lettre, on l’ajoute à la grille qui permet de stocker les cages temporairement. La grille finale correspond à un tableau composées d’élements ayant pour structure stcase. Si on trouve un point, on assigne la valeur 0 à la case correspondante (dans la grille finale cette fois ci). Si on trouve un nombre, on assigne sa valeur à la case correspondante (toujours dans la grille finale). Au même moment, on initialise par défaut tout les noms de cage à ! dans la grille finale, ce qui va nous permettre de les renommer plus facilement par la suite.
Partie 7: Formatage des entrées
// Formatage des entrées et renommage des cages for (int i = 0; i < h; i++) { // Parcour du tableau for (int j = 0; j < w; j++) { if(tab[i][j].cage=='!'){ // Si la cage à laquelle cette case appartient n'est pas encore renommée int teste[21][21]={0}; occ[c2].valeur=voisin(i,j,cages[i][j],0,teste,'#'+c,h,w); // On renomme toutes les cases de cette cage et on stock leur nombre occ[c2].cage='#'+c; // On met à jour le prochain nom disponible c++; c2++; if(c+'#'=='B'){ // Pour éviter les problèmes vis-à-vis des noms c+=25; } } } }
Dans cette dernière partie, on va parcourir la grille afin de renommer les cages, pour que chaque cage ai un nom différent, ce qui permet de faciliter le code d’autres fonctions. On va pour chaque case du tableau vérifier si la cage à laquelle elle appartient n’est pas renommée. Si elle n’est pas renommée, on va appeler la fonction voisin vue plus haut. Elle va permettre de renommer la cage concernée, et cela va appliquer le changement pour toutes les élement de la cage. C’est-à-dire que chaque case de la grille appartenant à la cage renommée sera bien mise à jour avec le nouveau nom. Ensuite, on va actualiser le nouveau nom que l’on peut donner à une cage, contenu dans la variable c. On rajoutera également une condition, car lorsque le nombre de cage est important, il est possible que l’on veuille donner un nom en lettre majuscule à une cage. Or, les anciens noms des cages sont également écrit en lettre majuscule. Il peut donc y avoir des conflits, car le programme va considérer les nouveaux noms en majuscule comme des anciens noms. Ainsi il ne renommera pas correctement les cages et la suite du programme ne pourra pas correctement fonctionner. C’est donc pour cela que l’on empêche le programme de renommer des cages avec des lettres majuscules.
Détail algorithmique de la méthode
Ce programme se base sur le principe de récursion, et appelle un certain nombre d’autres fonctions auxiliaires. Je vais tout d’abord présenter le principe générale de la récursion, puis je reviendrai plus en détail sur l’une des fonctions de mon code.
Principe général et fonction solve
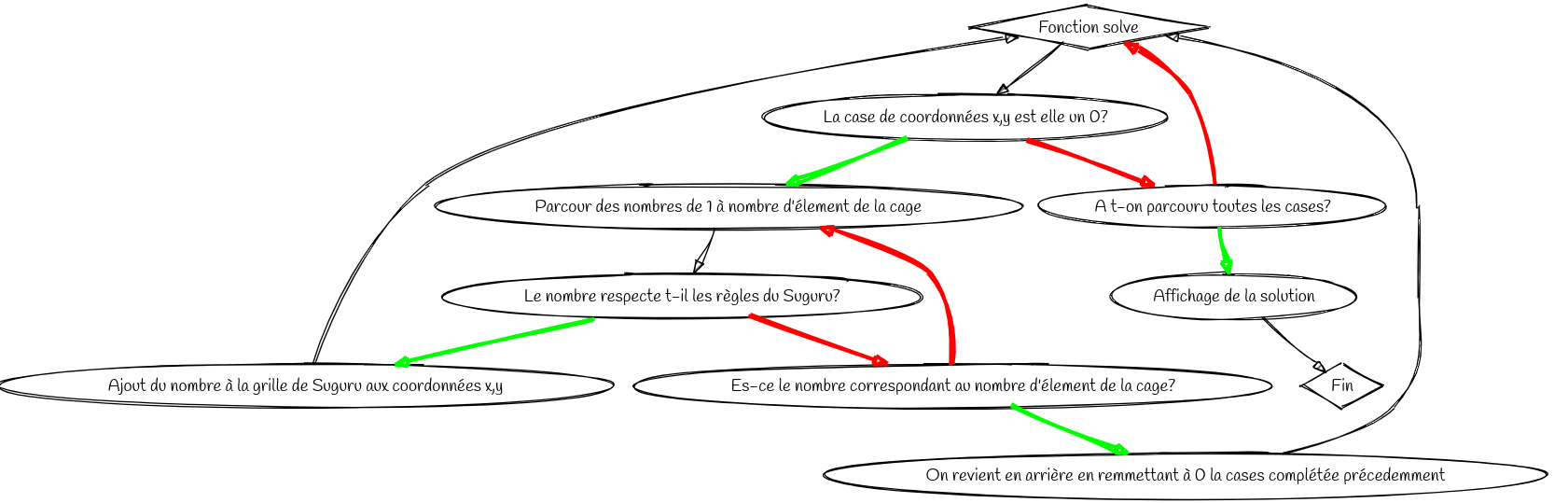
Cliquez ici pour agrandir
Dans le schéma ci dessus, les flèches rouges représentent un test négatif, et les vertes un test positif.
Tout d’abord revenons sur ce qu’est un mécanisme de récursion. Ce mécanisme consiste en l’appel d’une fonction à l’intérieur d’elle même. Une fonction récursive mal définie/codée peut donc engendrer un nombre infini d’appel. Mais ce mécanisme bien utilisé peut être très puissant et extrémement utile.
C’est le cas de cette fonction qui l’utilise afin de trouver la solution au Suguru de manière brute. C’est-à-dire qu’elle teste toutes les solutions possibles jusqu’à trouver la bonne. Dans cette fonction (solve()), on parcour le tableau, et dès que l’on trouve un 0, on essaye de remplir la case. Alors, on test tout les nombres de 1 au nombre d’élement d’une case. Pour que le test soit validé il faut que la fonction test renvoie 1. Dès que l’on trouve un nombre qui fonctionne, on le place dans la grille, puis on appelle à nouveau la fonction, jusqu’à ce que la grille soit remplie. Alors, si les nombres déjà placés bloquent la grille, les cases précedement remplies seront remises à 0, et les test seront fait avec d’autres nombres. Ainsi, suivant ce processus, la fonction ne s’arrétera que lorsque toute la grille sera remplie.
Fonction test
Nous allons maintenant nous intéresser à la fonction test et à son fonctionnement. Afin d’illustrer mes propos, voici ci dessous un schéma explicatif du fonctionnement de la fonction.
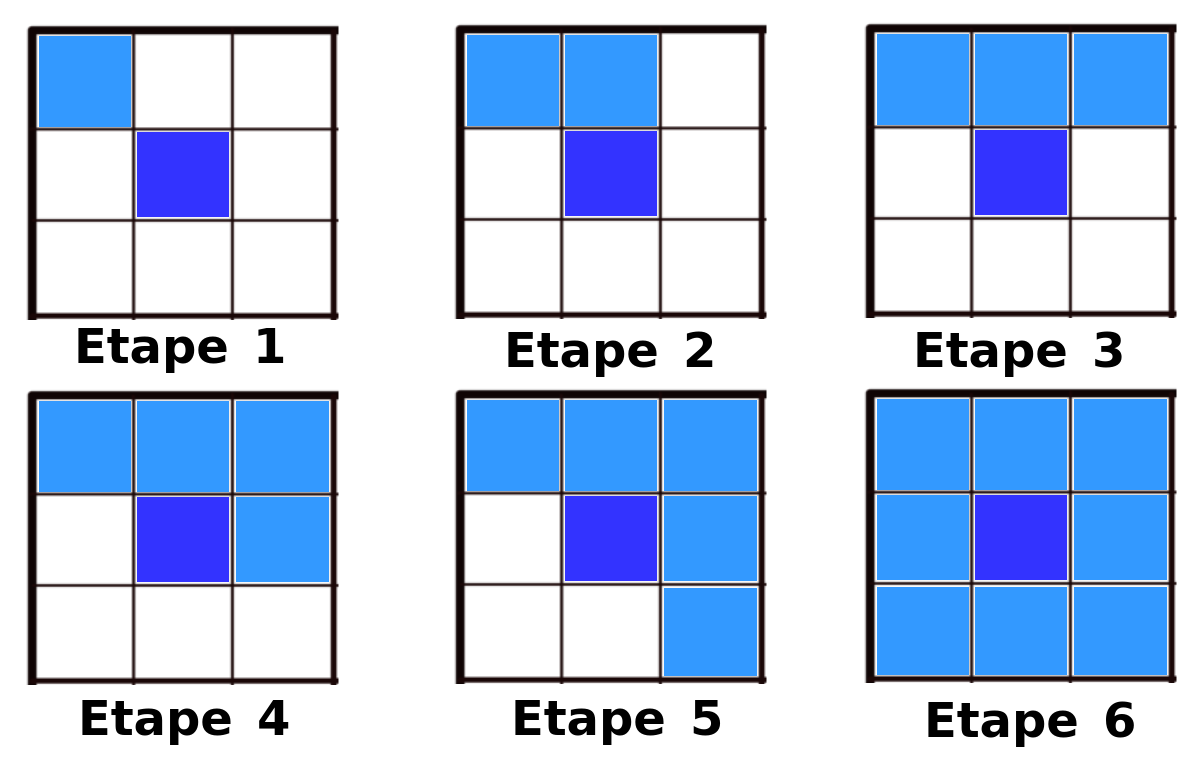
Cliquez ici pour agrandir
Dans le schéma ci dessus, la case que l’on veut remplir est en bleu foncé, et les cases déja testées en bleu clair.
Dans la première partie de la fonction, on va donc vérifier toutes les cases adjacentes à la case que l’on veut remplir. Les diagonales sont comprises. Si on considère que la case centrale a pour coordonnées (i,j), alors voici l’ordre dans lequel on regarde les cases:
- Etape 1: case (i-1,j-1)
- Etape 2: case (i-1,j)
- Etape 3: case (i-1,j+1)
- Etape 4: case (i,j+1)
- Etape 5: case (i+1,j+1)
- Etape 6: case (i+1,j-1)
Toutes les étapes ne sont pas représentées, mais cela permet d’avoir une meilleure idée du fonctionnement de la première partie de la fonction test.
Nous allons maintenant nous intéresser à la seconde partie de cette fonction, avec la vérification de la présence unique de chaque nombre dans une cage. Pour ce faire, voici ci dessous un schéma explicatif.
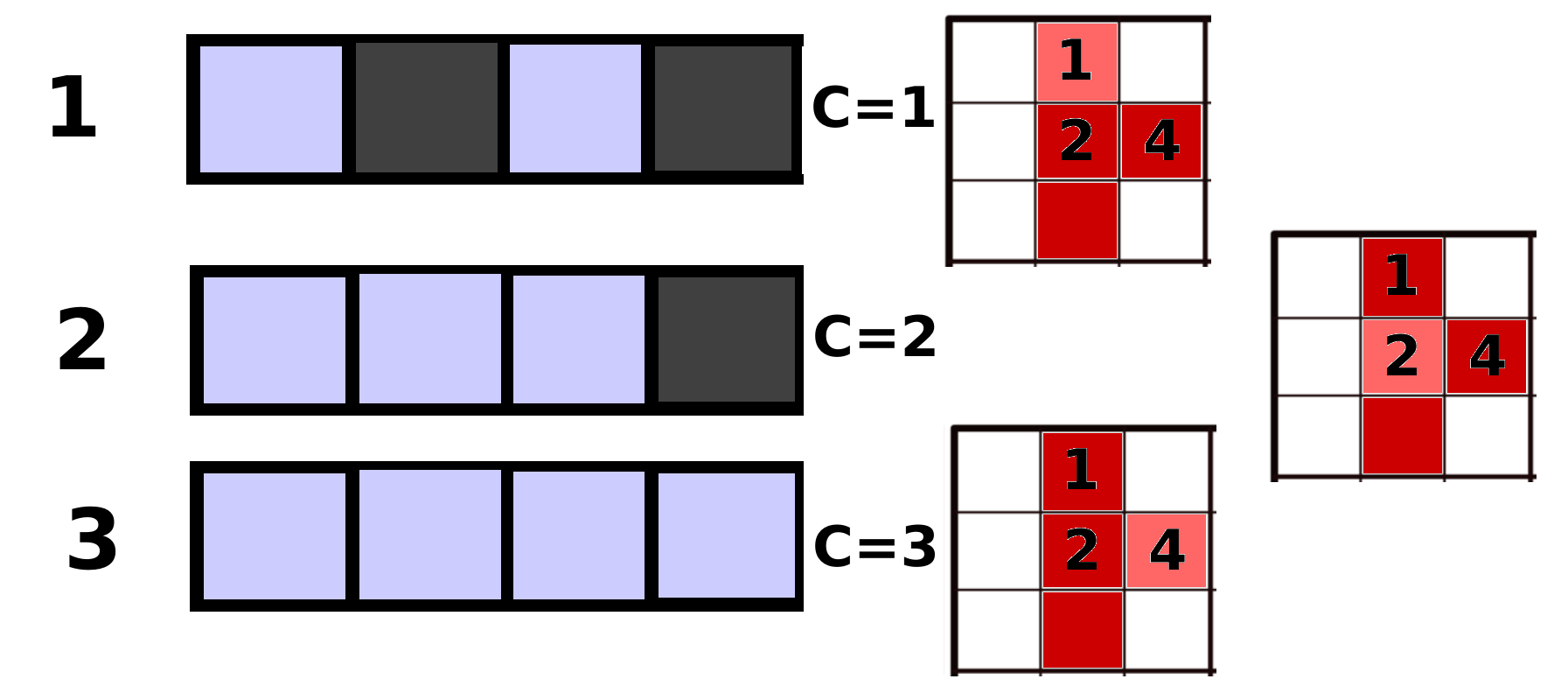
Cliquez ici pour agrandir
A gauche du schéma on retrouve le numéro des étapes, puis on observe un tableau, représentant le tableau verif, avec les cases foncées représentant une case de tableau avec la valeur 1, et les cases clairs représentant une case de tableau avec la valeur 0. Ensuite le troisième élement du schéma nous montres l’état du compteur (c). Enfin, nous avons un extrait du parcour de la grille de Suguru, avec en rouge la cage, et en rouge clair la case examiné lors de l’étape.
Le principe de cette vérification est simple. On initialise un tableau rempli de 1, de la même taille que le nombre d’élement de la cage. Puis, on met la case numéro n-1 à 0 (n étant le nombre que l’on souhaite ajouter à notre grille). Ensuite, on va parcourir la grille, et dès lors que l’on trouvera une case de valeur x appartenant à la cage, on mettra à 0 la case x-1 du tableau si elle ne l’est pas déja. En effet, si cette case est déja à 0, alors cela signifit qu’il y a deux nombres identiques dans une même cage, et donc que le nombre n’est pas valide. On renverra donc que le test n’est pas passé. Afin de s’arréter lorsque l’on a trouvé tout les élements de la cage, on met en place un compteur qui fera s’arréter la boucle si il atteint la valeur du nombre d’élement dans la cage (précisement moins un élement dû au fait que l’on ai déjà mis un 0 dans le tableau, il correspond au nombre que l’on souhaite vérifier). Ainsi, tout les tests seront passés et la fonction aura une valeur de retour de 1.
Prenons l’exemple du schéma. On souhaite tester si le nombre 3 peut être ajouter à la dernière case vide de la cage rouge. Lors de l’étape 1, le programme trouve la case de la cage avec la valeur 1. Ayant dès le départ mis à 0 la case du tableau de vérification correspondant au nombre que l’on souhaite ajouter, il y a deux cases à 0 dans le tableau (la case que l’on vient d’évoquer, et celle correspondant à la valeur 1). Le compteur est quand à lui incrémenté de 1, puisque l’on vient de trouver une case appartenant à la cage. Après avoir essayé plusieurs cases qui n’appartenaient pas à la cage, on arrive à l’étape 2. On met à 0 la case du tableau de vérification correspondante, et on incrémente le compteur de 1. Puis on répète le même processus jusqu’à l’étape 3, où le compteur prendra la valeur 3. Le compteur vaut le nombre d’élement de la cage rouge moins un, on arrête donc la boucle, et la fonction renvoi 1. Il est bien possible d’ajouter la valeur 3 à la case ciblée.
Code commenté ayant résolu le problème
Voici ci dessous le code complet m’ayant permis de résoudre le problème.
#include <stdlib.h> #include <stdio.h> #include <string.h> #include <stdbool.h> typedef struct st_case{ // Définition d'une structure représentant une case int valeur; char cage; }st_case; st_case tab[20][20]; // Grille de suguru char cages[20][20]; // Grille avec les cages uniquement st_case occ[100]; int w; int h; int test(int i, int j, int n, int occ){ // Fonction qui test la validité du nombre int y=0; int x=0; int count=0; // Test les nombres adjacent à la case que l'on souhaite remplir if((i!=0)&&(j!=0)&&(tab[i-1][j-1].valeur==n)){ // haut-gauche return 0; } if((i!=0)&&(tab[i-1][j].valeur==n)){ // haut return 0; } if((i!=0)&&(j!=w-1)&&(tab[i-1][j+1].valeur==n)){ // haut-droite return 0; } if((j!=0)&&(tab[i][j-1].valeur==n)){ // gauche return 0; } if((j!=w-1)&&(tab[i][j+1].valeur==n)){ // droite return 0; } if((i!=h-1)&&(j!=0)&&(tab[i+1][j-1].valeur==n)){ // bas-gauche return 0; } if((i!=h-1)&&(tab[i+1][j].valeur==n)){ // bas return 0; } if((i!=h-1)&&(j!=w-1)&&(tab[i+1][j+1].valeur==n)){ // bas-droite return 0; } int verif[10]; // Creation d'un tableau rempli de 1 for(int k=0;k<occ;k++){ verif[k]=1; } verif[n-1]=0; // Parcour de la grille while((y<h)&&(occ!=count)){ while((x<w)&&(occ!=count)){ if((tab[i][j].cage==tab[y][x].cage)&&(tab[y][x].valeur!=0)){ // Si le nombre appartient à la même cage que la case traitée et si le nombre n'est pas 0 if(verif[tab[y][x].valeur-1]==1){ // Si le nombre n'est pas déja présent dans la cage verif[tab[y][x].valeur-1]=0; // On l'ajoute à la liste des nombres présents count++; }else{ return -1; } } x++; } x=0; y++; } return 1; } int getocc(int y, int x){ // Permet de connaitre le nombre d'élement de chaque cage int c=0; for(c=0;c<100;c++){ if(tab[y][x].cage==occ[c].cage){ // Si on trouve dans la liste occ le nom de la cage dans laquelle se trouve la case x,y return occ[c].valeur; // On renvoi le nombre d'élement de la cage } } return 0; } void solve() { // Fonction récursive qui permet la résolution de la grille int y, x,n; for (y = 0; y < h; y++) { for (x = 0; x < w; x++) { if (tab[y][x].valeur == 0) { // Si la case que l'on regarde n'est pas remplie int occ=getocc(y,x); // On récupère le nombre d'élement de sa cage for(n = 1; n <= occ ; n++){ // On test tout les nombres possibles if (test(y, x, n, occ)==1){ // Si le test est positif tab[y][x].valeur = n; // On rempli la case avec la valeur solve(); // On rappel la fonction pour finir de compléter la grille tab[y][x].valeur = 0; // Remise à 0 de la case si mauvais choix } } return; } } } // Affichage du résultat for (int i = 0; i < h; i++) { for (int j = 0; j < w; j++) { printf("%d", tab[i][j].valeur); } printf("\n"); } exit(0); } int voisin(int i, int j, char name, int count,int teste[21][21],char new_name,int h,int w){ if ((cages[i][j]!=name)&&(cages[i][j]!=new_name)){ // Si l'élement testé n'appartient pas à la cage return count; } count++; // Ajoute 1 au compteur teste[i][j]=1; // Marque la case comme déja explorée tab[i][j].cage=new_name; // Renome la cage avec un nom unique cages[i][j]=new_name; // Renome la cage avec un nom unique if((i!=0)&&(teste[i-1][j]!=1)){ // Si on est pas sur le bord supérieur de la grille count=voisin(i-1 , j, name, count, teste, new_name,h,w) ; // On test la case du dessus } if((j!=0)&&(teste[i][j-1]!=1)){ // Si on est pas sur le bord gauche de la grille count=voisin(i , j-1, name, count, teste, new_name,h,w) ; // On test la case de gauche } if((j!=w-1)&&(teste[i][j+1]!=1)){ // Si on est pas sur le bord droit de la grille count=voisin(i , j+1, name, count, teste, new_name,h,w) ; // On test la case de droite } if((i!=h-1)&&(teste[i+1][j]!=1)){ // Si on est pas sur le bord inférieur de la grille count=voisin(i+1 , j, name, count, teste, new_name,h,w) ; // On test la case du dessous } return count; } int main(){ // Définition de compteurs int j,count,count2; int c=0; int c2=0; scanf("%d%d", &w, &h); fgetc(stdin); // Récupération des dimensions // Récupération des entrées for (int i = 0; i < h; i++) { char line[60]; scanf("%[^\n]", line); fgetc(stdin); j=0; count=0; count2=0; while(line[j]!='\0'){ if((line[j]>='1')&&(line[j]<='9')){ tab[i][count].valeur=line[j]-'0'; tab[i][count].cage='!'; count++; }else if(line[j]=='.'){ tab[i][count].valeur=0; tab[i][count].cage='!'; count++; }else if((line[j]<='Z')&&(line[j]>='A')){ cages[i][count2]=line[j]; count2++; } j++; } } // Formatage des entrées et renommage des cages for (int i = 0; i < h; i++) { // Parcour du tableau for (int j = 0; j < w; j++) { if(tab[i][j].cage=='!'){ // Si la cage à laquelle cette case appartient n'est pas encore renommée int teste[21][21]={0}; occ[c2].valeur=voisin(i,j,cages[i][j],0,teste,'#'+c,h,w); // On renomme toutes les cases de cette cage et on stock leur nombre occ[c2].cage='#'+c; // On met à jour le prochain nom disponible c++; c2++; if(c+'#'=='B'){ // Pour éviter les problèmes vis-à-vis des noms c+=25; } } } } solve(); return 0; }
Présentation des tests
Afin de coder ce programme et de le valider, il a fallut passer plusieurs tests. Alors voici ci dessous les tests qui m’ont permi de résoudre ce problème.
Test 1
Test 2
- Entrée
8 8 G. G. G. M. M5 R. R. G. R. R. R. R. M. M. G. G. G. M. R. C. C4 M. G. R. G. M. M. C. C. B. B. R. G. M. M. C. B. B. R. R. R. B. G. G. B. G. G4 G. R. B. B. G. R. R. G. G. R. B. B. G. G. R. R. B.
- Résultat
============Test passe============ ==============Sortie============== 21345121 34212343 21534121 34212354 15354123 32412341 15354152 24123231 ==================================
Ce second test permet de commencer à débugguer le code.
Test 3
- Entrée
15 10 R. B5 B. B4 B. R. R4 R. B. B5 B. R1 R4 R. B. R4 R. B1 B. R. R6 G. R. B. G4 R. R. G. R6 B1 R. R6 R. G5 G. G. G2 B. B. G3 G. G. G. B. B4 B. B1 B. G. B. B. B. R1 R. R6 C1 C. C. B5 B. B5 B. R. R. R. B. R. R. G. R. C. C6 R. R1 R. B. R. R. C. R. B6 B. G. G. G. C. R. R. G. R. G2 G. C. C1 C. C. R. R3 G. B. B. G. G. G. G4 C. G4 G. C. B3 B. B4 R. R6 R. B. R. R. R. G. C2 C. C. B. B. R. B. G. R. G. R. R. B. R. B. C. C6 R3 R5 R. R. R. G5 G. G. G. B6 B2 B4 B.
- Résultat
============Test passe============ ==============Sortie============== 156423423561452 431316151423261 562543242356134 213621515613456 542143232426214 636356451353536 215142134212614 343635426534325 251212634215163 463564151646245 ==================================
Dans ce troisième test, il faut commencer à optimiser le code afin que le temps d’execution ne soit pas trop grand. Il faut aussi qu’aucun cas particulier ne soit oublié.
Test 4
- Entrée
20 20 R. R6 R. B6 B. R. B. B6 B. R. R. B. B5 R6 R. R1 G. G. G. B. R3 B. B. B2 R. R. R. B. B. B. G6 B. B. R2 R. R. B. G. G. B2 R5 G. B. G. R. G. G3 R. R. G. G. B3 B. G. G. G. B. B5 R. B5 R. G. G5 G. R. G. G. R. B. G. B. R. R. R. G. G. B. B. R. B. B. B. G. R. B. B. G. B4 B. G. B4 B. R. R. Y. R4 R. B6 R. B. B5 R. R3 R1 R. Y. G. B. B. G. B. B6 Y. Y. Y. Y. R. R. Y. B4 B. B. G. R. Y. Y. Y. G1 B. R. B. R. B. B5 B. R. R. G. Y. Y. R. B. G4 G. Y2 Y. R. G3 G. R. R. R5 G. B. B. G3 G. G. G. Y. R. R. G. G. R. R. R. G. B6 B. R. G4 G. G1 B6 R. G. B. B. G. R. B3 G. B. B5 R. G. G5 B. B. B2 G. R. G. R. R. R2 R. G. G. B. B. R. B. B1 Y. Y. R. R. G. B. R6 R. R. B. Y. Y. R. G3 G. B. B5 R. B. G. R. Y. R. G. G4 R. R. B. B. B3 B. Y4 Y. Y. Y. G. B. R6 B. G5 R. Y. Y3 G. Y. Y. Y. B. R. G. G. G. G. R1 R4 G. G. R. R3 G. G. R. Y. G. G. Y. G. R. R4 R. Y. G5 G. R3 R. G. G. B. R. G. G. R4 B. B. B6 G. G5 R. R2 Y. Y. Y. B1 R. R. R. B5 B. B. B. B. R. R6 B. B. G2 G. G. B. Y. Y1 B. B. B5 G. R. G. G. G. G. R. R. G. G. B3 R1 B. B6 B. B. R. B. B6 Y. G. R. B. G6 G. R. G2 G. G. G6 R. R. B. G. R. R3 R4 R. Y. Y. G. B1 B. B. R. R4 R. R3 B. B. R4 R. G. G. G. R. G. G. Y5 Y. R. B. B. G. G. G. G. R. B. B3 R. G5 G1 B. B. B. G. G4 G. Y. R.
- Résultat
Mon code ne passe pas le dernier test. En effet, lorsque la grille devient très grande, mon code devient inefficace ou crée une boucle infinie. Malgré de nombreux essais, je n’ai malheureusement pas réussi à suffisemment l’améliorer. Ce dernier test m’a tout de même permi de supprimer des erreurs et de modifier des morceaux de codes inutiles ou trop inefficaces.
Valgrind
Afin d’être certain de ne pas avoir de problèmes de mémoire et autres, que le compilateur n’aurait pas détecté, on utilise valgrind.
valgrind ./suguru < sugurutest/test3
Cliquez ici pour agrandir
Le programme présenté passe bien valgrind pour les 3 premiers tests.
Bilan de ce travail
Malgré que je n’ai pas réussi à aboutir à un code passant tout les tests, ce travail a tout de même eu un certain nombre d’aspect positifs. En effet, la conception de ce programme m’a forcé à réfléchir à la complexité temporelle de mon algorithme. J’ai donc dû l’optimiser un minimum afin qu’il puisse passer les premiers tests. De plus, le format des entrées m’a obligé à manipuler des chaines de caractère de manière plus approfondie, et m’a également permi de travailler avec les structures de données.
