Sudoku
Table of Contents


1. Introduction
1.1. Introduction Sudoku solver
Votre programme doit générer une solution à un sudoku 9x9. Un sudoku est un carré latin qui comporte les chiffres 1 à 9 ,dans chaque ligne, colonne et carré et ne doivent pas apparaitres plus d’une fois dans chaque ligne, colonne et carré 3x3.
1.2. Introducion à killer sudoku
Après le puzzle sudoku. Killer sudoku ajoute une nouvelle règle avec les cages. Une cage est un groupe de cellules dont la somme doit être égale à la valeur de la cage. Les nombres ne peuvent pas se répéter dans les cages. Et chaques somme des cages doivent être agale a une valeur fixé par l’énoncé.
1.3. Introduction à Suguru solver
Suguru (également connu sous le nom de Tectonics) est un jeu de réflexion similaire au Sudoku. Le puzzle est composé de différentes zones, appelées cages. Chaque cage comporte de 1 à 6 cellules et contient les chiffres de 1 à la taille de la cage. C’est-à-dire qu’une cage à 2 cellules contient les chiffres 1 et 2, et une cage à 5 cellules contient les chiffres 1 à 5. Les cellules adjacentes, même en diagonale, ne peuvent jamais contenir le même chiffre.
2. Solution expliquée
2.1. Sudoku solver
Pour cette exercice, j’ai crée 3 fonctions de vérification, “ligneValide” qui prends la valeur actuelle et la ligne actuelle ainsi que le tableau et vérifie si la valeur actuelle n’est pas déjà présente sur la ligne, si oui elle renvoie 0 sinon 1. une fonction “colonneValide” qui vérifie si la valeur actuelle est déjà dans la colonne j, et la fonction “sousGrilleValide”, qui regarde si la valeurs actuelle est déjà dans la sous grille. Enfin la fonction “estvalide” qui va appeler les trois fonction ci-dessus avec chaque valeurs de 1 à 9 puis si toutes les valeurs ne fonctionnent pas, alors on reviens avec la recursivité à la case d’avant, on appelle ça du back-tracking.
#include <stdlib.h> #include <stdio.h> #include <string.h> #include <stdbool.h> #define M 9 //test si la ligne est valide pour une k valeur int ligneValide(int k, int grille[M][M], int i) { for (int j=0; j < 9; j++) if (grille[i][j] == k) return 0; return 1; } //test si la colonnes est valide pour une k valeur int colonneValide(int k, int grille[M][M], int j) { for (int i=0; i < 9; i++) if (grille[i][j] == k) return 0; return 1; } // test si la sous grille est valide pour une k valeur int sousGrilleValide(int k, int grille[M][M], int i, int j) { int i2 = i-(i%3), j2 = j-(j%3); for (i=i2; i < i2+3; i++) for (j=j2; j < j2+3; j++) if (grille[i][j] == k) return 0; return 1; } // test des trois fonctions en recursivité afin de tester avec toutes les valeurs int estvalide(int grille[M][M], int position) { if (position == 9*9) return 1; int i = position/9, j = position%9; if (grille[i][j] != 0) return estvalide(grille, position+1); for (int k=1; k <= 9; k++) { if (ligneValide(k,grille,i) && colonneValide(k,grille,j) && sousGrilleValide(k,grille,i,j)) { grille[i][j] = k; if (estvalide(grille, position+1) ) return 1; } } grille[i][j] = 0; return 0; } int main() { int grille[M][M]; for (int i = 0; i < 9; i++) { char line[10]; scanf("%[^\n]", line); fgetc(stdin); for (int j=0; j<9; ++j) { grille[i][j] = line[j] - '0'; } } estvalide(grille, 0); for (int i=0; i<9; ++i) { for (int j=0; j<9; ++j) { printf("%d", grille[i][j]); } printf("\n"); } return 0; }
2.2. Killer Sudoku solver
Pour cette exercice, j’ai repris le code de sudoku solver et j’ai ranger dans un nouveau tableau la grille des groupes. J’ai ajouter une fonction “memeCageValide” qui elle même, appele “IsFullForAGroup” qui determine si telle groupe de lettre à été remplie entièrement. Si c’est le cas, alors on vient tester si la somme Des cages est la même que c’elle envoyer dans l’input, et ce grace à la fonction “sommDeCage” qui me permet de déterminer la valeur de la cage.
#include <stdlib.h> #include <stdio.h> #include <string.h> #include <stdbool.h> #define M 9 //test si la ligne est valide pour une k valeur int ligneValide(int k, int grille[M][M], int i) { for (int j=0; j < 9; j++) if (grille[i][j] == k) return 0; return 1; } //test si la colonnes est valide pour une k valeur int colonneValide(int k, int grille[M][M], int j) { for (int i=0; i < 9; i++) if (grille[i][j] == k) return 0; return 1; } // test si la sous grille est valide pour une k valeur int sousGrilleValide(int k, int grille[M][M], int i, int j) { int i2 = i-(i%3), j2 = j-(j%3); for (i=i2; i < i2+3; i++) for (j=j2; j < j2+3; j++) if (grille[i][j] == k) return 0; return 1; } // test des trois fonctions en recursivité afin de tester avec toutes les valeurs int indiceLettreAlphabet(char lettre) { if (lettre >= 'a' && lettre <= 'z') { return lettre - 'a'; // Pour les lettres minuscules ('a' vaut 0, 'b' vaut 1, ..., 'z' vaut 25) } else if (lettre >= 'A' && lettre <= 'Z') { return lettre - 'A' + 26; // Pour les lettres majuscules ('A' vaut 26, 'B' vaut 27, ..., 'Z' vaut 51) } else { return -1; // Si la lettre n'est ni minuscule ni majuscule, retourner -1 (erreur) } } int IsfullForAGroupe(int grille[M][M],char alphabetGrille[M][M],char groupe_de_cage,int i,int j) { for (int x=0; x < 9; ++x){ for (int y=0; y < 9; ++y){ if (alphabetGrille[x][y] == groupe_de_cage){ if(x==i && y == j) { } else if(grille[x][y]==0) { return 0; } } } } return 1; } //test si la colonnes est valide pour une k valeur int SameNumberForACage(int k, int grille[M][M],char alphabetGrille[M][M],int groupe_de_cage) { for (int x=0; x < 9; ++x){ for (int y=0; y < 9; ++y){ if (alphabetGrille[x][y] == groupe_de_cage){ if(k==alphabetGrille[x][y] ) { return 1; } } } } return 0; } int sommeDeCage(int k,int grille[M][M], int i, int j,char alphabetGrille[M][M],char groupe_de_cage) { int s=0; for (int x=0; x < 9; ++x){ for (int y=0; y < 9; ++y){ if(alphabetGrille[x][y]==groupe_de_cage) { if(x!=i && y!=j) { s+=grille[x][y]; } } } } return s; } int memeCageValide(int k,int grille[M][M], int i, int j,char alphabetGrille[M][M],int tableau_minuscules[]) { char groupe_de_cage = alphabetGrille[i][j]; int max = tableau_minuscules[indiceLettreAlphabet(groupe_de_cage)]; int valeur_actuelle=0; //verifier si toute les cages sont remplies if(SameNumberForACage(k,grille,alphabetGrille,groupe_de_cage)) { return 0; } if(IsfullForAGroupe(grille,alphabetGrille,groupe_de_cage,i,j)) { if(sommeDeCage( k, grille, i, j, alphabetGrille,groupe_de_cage)!=max) { return 0; } } else { if(sommeDeCage( k, grille, i, j, alphabetGrille,groupe_de_cage)>=max) { return 0; } } return 1; } int estvalide(int grille[M][M], int position,char alphabet_grille[M][M],int tableau_minuscules[]) { if (position == 9*9) return 1; int i = position/9, j = position%9; if (grille[i][j] != 0) return estvalide(grille, position+1,alphabet_grille,tableau_minuscules); for (int k=1; k <= 9; k++) { if (ligneValide(k,grille,i) && colonneValide(k,grille,j) && sousGrilleValide(k,grille,i,j) && memeCageValide(k,grille,i,j,alphabet_grille,tableau_minuscules)) { grille[i][j] = k; if (estvalide(grille, position+1,alphabet_grille,tableau_minuscules) ) { return 1; } } } grille[i][j] = 0; return 0; } void rangerValeurs(char *str, int *tab) { char *token; const char *delim = " "; token = strtok(str, delim); // Découper la chaîne en tokens int i = 0; while (token != NULL) { // Récupérer la partie après le '=' et la convertir en entier pour la stocker dans le tableau tab[i] = atoi(token + 2); token = strtok(NULL, delim); i++; } } int main() { int grille[M][M]; char alphabet_grille[M][M]; int tableau_minuscules[251]; for (int i = 0; i < 9; i++) { char grid_line[10]; char grid_cages[10]; scanf("%s%s", grid_line, grid_cages); fgetc(stdin); for (int j=0; j<9; ++j) { if (grid_line[j] == '.') { grid_line[j] = '0';} grille[i][j] = grid_line[j] - '0'; alphabet_grille[i][j]=grid_cages[j]; } } char cages[251]; scanf("%[^\n]", cages); rangerValeurs(cages, tableau_minuscules); estvalide(grille, 0,alphabet_grille,tableau_minuscules); for (int i=0; i<9; ++i) { for (int j=0; j<9; ++j) { printf("%d", grille[i][j]); } printf("\n"); } return 0; }
2.3. Suguru solver
N’étant pas arriver à faire fonctionner certaines de mes fonctions je vais donc vous montrer l’algorithme synthéthique sous forme de graph.
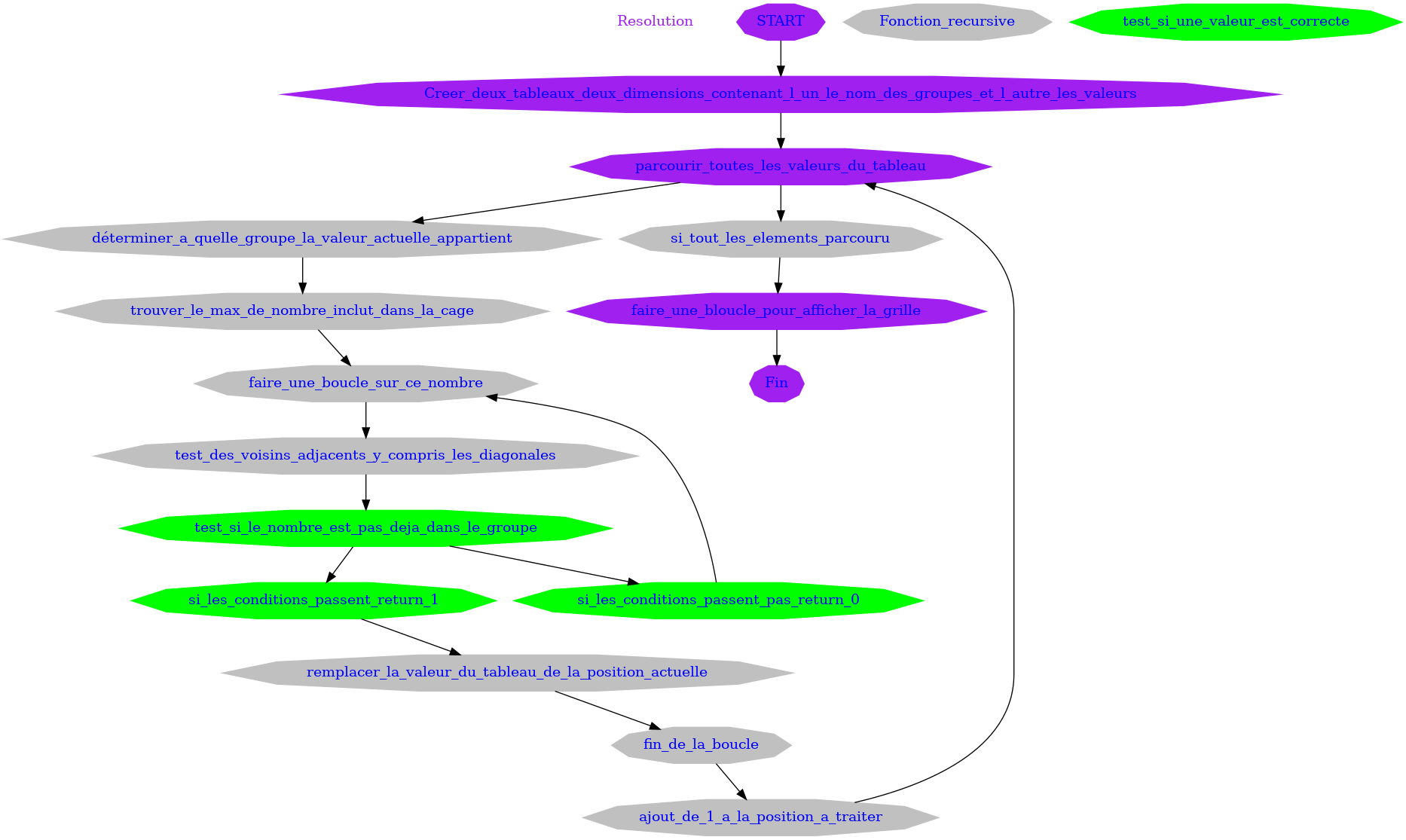
(sans bug d’affichage)

3. Tests et exécutions
3.1. Sudoku Solver
3.1.1. World’s Hardest Sudoku
Test avec comme entrées
gcc -Wextra -Wall -Werror sudoku1.c ./a.out 800000000 003600000 070090200 050007000 000045700 000100030 001000068 008500010 090000400
voici le résultat:
| 123874569 |
| 567932184 |
| 849651237 |
| 916247853 |
| 358196472 |
| 472385916 |
| 291768345 |
| 685423791 |
| 734519628 |
3.2. Sudoku Killer
3.2.1. exemple de Test
Test avec comme entrées
gcc -Wextra -Wall -Werror sudoku2.c ./a.out 856..1..2. aabbccdde ..72..68. afghhiide ..2.87.15 jfggklmme ......3.9 jjgnklopp .7....2.. qqgnooorr 9.634.8.. stuuvwwxx 2.9..8... stuuvvwyz ..41.2... sAuuByyyz .8.4...3. CADDBEEFF a=12 b=17 c=4 d=14 e=15 f=13 g=19 h=7 i=10 j=16 k=10 l=13 m=10 n=15 o=15 p=13 q=11 r=11 s=18 t=3 u=28 v=15 w=20 x=8 y=22 z=12 A=11 B=13 C=6 D=9 E=10 F=5
voici le résultat:
| 560010020 |
| 7200680 |
| 2087015 |
| 309 |
| 70000200 |
| 906340800 |
| 209008000 |
| 4102000 |
| 80400030 |
4. solutions de la communauté
4.1. Sudoku Solver
Dans la solution de Amnesix, il reprends le principe de back-tracking mais il détecte en plus les cases vides à remplir ce qui lui permet de gagner un peu de temps sur l’exécution.
#include <stdlib.h> #include <stdio.h> #include <string.h> #include <stdbool.h> static char table[9][9]; // Cherche une case vide int chercheVide(int *x, int *y) { int r, c; for (c=0; c<9; c++) for (r=0; r<9; r++) if (table[r][c] == 0) { *x=r; *y=c; return 1; } return 0; } // Vérifie si une valeur peut-être jouée sur une case donnée int isOk(int r, int c, int val) { int i, j; for (i=0; i<9; i++) { if (table[i][c] == val) return 0; if (table[r][i] == val) return 0; } int rd = 3*(r/3); int cd = 3*(c/3); for (i=rd; i<rd+3; i++) for (j=cd; j<cd+3; j++) if (table[i][j] == val) return 0; return 1; } /** * Résolution de la grille courante par force brute. * Fonction récursive. */ int brut() { int i; int r=0, c=0; if (!chercheVide(&r, &c)) return 1; for (i=9; i>0; i--) { if (isOk(r, c, i)) { table[r][c] = i; if (brut()) return 1; table[r][c] = 0; } } return 0; } int main() { for (int i = 0; i < 9; i++) { char line[10]; scanf("%[^\n]", line); fgetc(stdin); for (int j = 0; j < 9; j++) { table[i][j] = line[j] - '0'; } } brut(); for (int i = 0; i < 9; i++) { for (int j = 0; j < 9; j++) { printf("%d", table[i][j]); } printf("\n"); } return 0; }
4.2. Killer Sudoku Solver et Suguru
Aucune solution en C n’est disponible pour ces deux exercices :/