Des nains sur des épaules de géants
Table of Contents


1. Introduction text generation
La citation “Des nains sur des épaules de géants” se réfère à l’importance pour tout homme de s’appuyer sur les travaux de ses prédécesseurs.
À la lecture des textes, on ne glane qu’une petite partie de cette dépendance : telle personne a influencé telle autre personne. On apprendra par la suite que cette seconde personne en a, à son tour, influencé une troisième, et ainsi de suite.
2. Le but
Le but de cette exercice est de retrouver la chaine d’influence la plus grande parmis un arbre d’influence donnée.
3. Solution expliquée
Pour cette exercice il nous faut parcourir tout les couples de données, dans mon code, je crée alors deux tableaux, un nommé valeur qui contiendra uniquement la première valeur du couple d’une liaison, puis une autre nommé next qui lui contiendra uniquement la deuxième valeur du couple d’une liaison. Ensuite j’utilise une fonction TrouverLeDebut qui va stocker dans un tableaux tout les numéros qui sont en début de chaine. Après avec une fonction récursive je parcours les couples liées avec le numéro de la tête de chaine, tout en ajoutant 1 au compteur de liaison, puis je détermine le plus grand avec une simple fonction max.
Enfin, je me retrouve avec un tableau de tout les maximum de tout les chemins avec les différents début, je fait alors un simple max() de tout ces chemins.
#include <stdlib.h> #include <stdio.h> #include <string.h> #include <stdbool.h> #define M 10 int est_present(int nombre, int liste[], int taille) { for (int i = 0; i < taille; i++) { if (liste[i] == nombre) { return 1; // Retourne 1 si l'élément est trouvé } } return 0; // Retourne 0 si l'élément n'est pas trouvé } void trouver_indices(int liste[], int taille, int element, int indices[]) { int nb_indices_trouver = 0; for (int i = 0; i < taille; ++i) { if (liste[i] == element) { indices[nb_indices_trouver] = i; // Ajout de l'indice trouvé nb_indices_trouver++; } } // Réallocation de la mémoire pour réduire la taille du tableau return; } // Fonction pour trouver un élément présent dans la première liste mais pas dans la deuxième int TrouverLeDebut(int liste1[], int liste2[], int taille, int d[]) { int nb=0; for (int i = 0; i < taille; i++) { if (!est_present(liste1[i], liste2, taille)) { d[nb]= liste1[i]; // Retourne l'élément trouvé nb++; } } return nb; // Retourne -1 si aucun élément n'est trouvé } int trouver_max(int tableau[], int taille) { int max = tableau[0]; // Supposons que le premier élément est le maximum // Parcours du tableau pour trouver le maximum for (int i = 1; i < taille; ++i) { if (tableau[i] > max) { max = tableau[i]; // Mettre à jour le maximum si une valeur plus grande est trouvée } } return max; } int rechercheRecursiv(int recherche,int liste1[],int liste2[],int max,int taille) { int indices[M]={-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}; trouver_indices(liste1,taille,recherche,indices); int z=0; int rep[M]={max,0,0,0,0,0,0,0,0,0}; while(indices[z]>=0) { rep[z]=rechercheRecursiv( liste2[indices[z]], liste1, liste2,max+1, taille); z++; } return trouver_max(rep,M); } int main() { int valeur[M]; int next[M]; // the number of relationships of influence int n; scanf("%d", &n); for (int i = 0; i < n; i++) { // a relationship of influence between two people (x influences y) int x; int y; scanf("%d%d", &x, &y); valeur[i]=x; next[i]=y; } int d[M]; //tout les debut possibles int s[M]; //resultat des différents courants //trouver les debuts int nbTours=TrouverLeDebut(valeur,next,n,d); for(int i =0;i<nbTours;++i) { // trouver tout les resultat des differnets courants s[i]=rechercheRecursiv(d[i],valeur,next,1,n); } // The number of people involved in the longest succession of influences // prendre le max des resultats printf("%d\n",trouver_max(s,M)); return 0; }
4. Tests et exécutions
4.1. Test numéro1
Les entrées sont
gcc -Wextra -Wall -Werror dwarf.c ./a.out 3 1 2 1 3 3 4
Ce test est assez simple, il suffit de faire le max entre deux branches. voici le résultat:
1106483657
Et voici le graph du test:
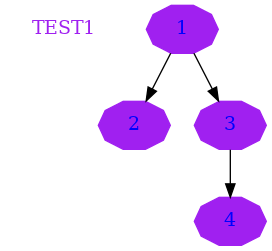
4.2. Test numéro2
Les entrées sont
gcc -Wextra -Wall -Werror dwarf.c ./a.out 8 1 2 1 3 3 4 2 4 2 5 10 11 10 1 10 3
Ce test complexifie l’arbre en mettant la valeur 10 comme tête de liaison Et voici le résultat:
32753
Et voici le graph du test:
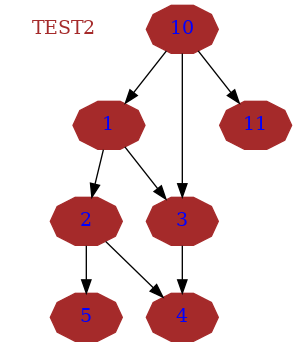
4.3. Test numéro3
Les entrées sont
gcc -Wextra -Wall -Werror dwarf.c ./a.out 4 2 3 8 9 1 2 6 3
Cette fois ci l’arbre est plus complexe puisqu’il à plusieurs débuts Et voici le résultat:
3
Voici le graph du test:
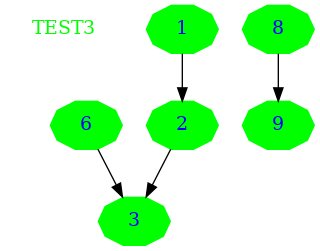
4.4. Test numéro4
Les entrées sont
gcc -Wextra -Wall -Werror dwarf.c ./a.out 9 7 2 8 9 1 6 6 9 1 7 1 2 3 9 2 3 6 3
Ce test est comme celui précédent mais avec plus de valeurs Et voici le résultat:
5
Voici le graph du test:
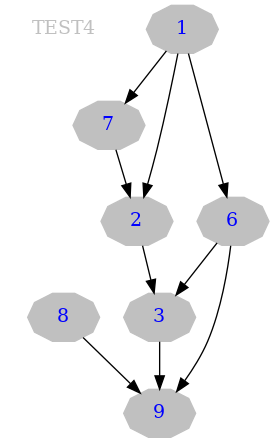
5. solutions de la communauté
Dans la solution de Kirbiby, il reprends le même principe que moi, avec une fonction max et une autre récursive qui parcours tout les couples. La diférence étant que Kirbiby range ses données dans une structure contenant un tabelau de tout les voisin de chaques noeuds.
#include <stdlib.h> #include <stdio.h> #include <string.h> #define MAX_INT 10000 int max(int a, int b){return a>b?a:b;}; typedef struct _noeud{ int nVoisins; int* voisins; } Noeud; Noeud arbre[MAX_INT]; int H[MAX_INT]; int hauteur(int noeud){ if (!H[noeud]){ int ans = 0; for (int j=0; j<arbre[noeud].nVoisins;j++) ans = max(ans, hauteur(arbre[noeud].voisins[j])); H[noeud] = 1 + ans; } return H[noeud]; } int main() { int n, x; scanf("%d", &n); for (int i = 0; i <n; i++){ scanf("%d", &x); arbre[x].nVoisins++; arbre[x].voisins = realloc(arbre[x].voisins, arbre[x].nVoisins); scanf("%d", &arbre[x].voisins[arbre[x].nVoisins-1]); } int ans = 0; for (int i = 0; i <MAX_INT; i++) ans = max(ans, hauteur(i)); printf("%d\n", ans); }