Sudoku
Table of Contents
1. Sudoku Solver
1.1. Présentation
Le but de ce codingame est de résoudre un sudoku.
1.1.1. Input
Une grille de sudoku de départ avec des 0 indiquant les cases vides.
1.1.2. Output
La grille de sudoku pleine.
1.2. Résolution
1.2.1. Programme principale
int main() { int grid[L][L]; char line[10]; for (int i = 0; i < 9; i++) { scanf("%[^\n]", line); fgetc(stdin); append_text(line, *grid, i); } int i, j; solver(*grid, 0); for (i = 0; i < 9; ++i) { for (j = 0; j < 9; ++j) { printf("%d", grid[i][j]); } printf("\n"); } return 0; }
On s’occupe d’abord de récupérer la grille et de la stocker dans la matrice grid. On applique ensuite la fonction solver à la grille qui va nous la remplir. On s’occupe enfin d’afficher la grille.
1.2.2. Fonction Solver
int solver(int *grid, int i) { int poss_number; int line_id, column_id; if (i == L * L) { return 1; } line_id = i / L; column_id = i % L; if (!grid[i]) { for (poss_number = 1; poss_number < 10; ++poss_number) { if (is_possible(line_id, column_id, grid, poss_number)) { grid[i] = poss_number; if (solver(grid, i + 1)) { return 1; // It's possible to place the number } } grid[i] = 0; } return 0; // No possibilities } return solver(grid, i + 1); // Box different to 0 }
La fonction prend en paramètre la grille de sudoku et l’indice d’une case. Voici l’algorithme :
- On teste si la case est vide
- On teste chaque valeur de 1 à 9 pour cette case.
- S’il est possible de placer le nombre (is\possible), on le place et on appelle la fonction solver en ajoutant 1 à l’indice.
- On renvoie 1
- S’il est possible de placer le nombre (is\possible), on le place et on appelle la fonction solver en ajoutant 1 à l’indice.
- On teste chaque valeur de 1 à 9 pour cette case.
Ainsi, En partant de la première case, s’il est possible de placer un nombre sans erreur jusqu’à la dernière case, alors la grille est remplie et juste.
En d’autres termes, on teste toutes les combianisons possibles jusqu’à trouver la bonne.
1.2.3. Fonction is\possible
int is_possible(int i_line, int i_column, int *grid, int number) { int i; int line[L]; int column[L]; int square[L]; get_line(i_line, grid, line); get_column(i_column, grid, column); get_square(i_line, i_column, grid, square); for (i = 0; i < L; ++i) { if (line[i] == number || column[i] == number || square[i] == number) { return 0; } } return 1; }
Cette fonction renvoie 1 si il est possible de placer le nombre donné sur la case choisie. Pour cela :
- On récupère tout les nombres de la ligne
- On récupère tout les nombres de la colonne
- On récupère tout les nombres de la case de 9 cases
Enfin on regarde si le nombre que l’on veut placer l’est déjà.
1.3. Code complet
#include <math.h> #include <stdio.h> #define L 9 void get_line(int line_id, int *grid, int *line) { int i; for (i = 0; i < L; ++i) { line[i] = grid[line_id * L + i]; } } void get_column(int column_id, int *grid, int *column) { int i; for (i = 0; i < L; ++i) { column[i] = grid[i * L + column_id]; } } void get_square(int line, int column, int *grid, int *square) { int i; int L_root = sqrt(L); for (i = 0; i < L; ++i) { square[i] = grid[(line / L_root * L_root + i / L_root) * L + (column / L_root * L_root + i % L_root)]; } } int is_possible(int i_line, int i_column, int *grid, int number) { int i; int line[L]; int column[L]; int square[L]; get_line(i_line, grid, line); get_column(i_column, grid, column); get_square(i_line, i_column, grid, square); for (i = 0; i < L; ++i) { if (line[i] == number || column[i] == number || square[i] == number) { return 0; } } return 1; } void append_text(char *line, int *grid, int line_id) { int i; for (i = 0; i < L; ++i) { grid[line_id * L + i] = line[i] - 48; } } int solver(int *grid, int i) { int poss_number; int line_id, column_id; if (i == L * L) { return 1; } line_id = i / L; column_id = i % L; if (!grid[i]) { for (poss_number = 1; poss_number < 10; ++poss_number) { if (is_possible(line_id, column_id, grid, poss_number)) { grid[i] = poss_number; if (solver(grid, i + 1)) { return 1; // It's possible to place the number } } grid[i] = 0; } return 0; // No possibilities } return solver(grid, i + 1); // Box different to 0 } int main() { int grid[L][L]; char line[10]; for (int i = 0; i < 9; i++) { scanf("%[^\n]", line); fgetc(stdin); append_text(line, *grid, i); } int i, j; solver(*grid, 0); for (i = 0; i < 9; ++i) { for (j = 0; j < 9; ++j) { printf("%d", grid[i][j]); } printf("\n"); } return 0; }
1.4. Tests
1.4.1. Test facile
2. Killer Sudoku Solver
2.1. Présentation
You may know the sudoku puzzle. Killer sudoku adds a new rule with cages. A cage is a group of cells, the sum of which must equal the cage value. Numbers cannot repeat within cages.
Here are the 4 rules of killer sudoku:
- Each row must have numbers from 1 to 9 with no repetition
- Each column must have numbers from 1 to 9 with no repetition
- Each region (3x3 square) must have numbers from 1 to 9 with no repetition
- Each cage’s cell numbers must sum to the cage value, with no repetition among numbers
Vous connaissez maintenant les règles du sudoku comme votre poche. Il est donc temps de complexifier un peu l’affaire.
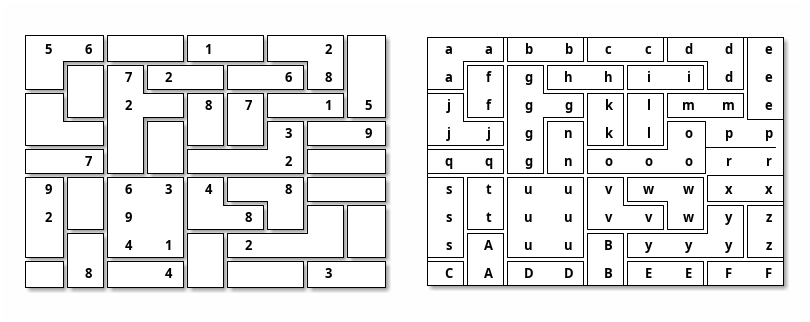
Comme vous pouvez le voir sur l’exemple ci-dessous, il y a maintenant des cages dans la grille de sudoku. Les règles restes inchangées, seulement, la somme de chaque case doit être égale a une valeur défini au préalable.
2.1.1. Exemple d’input
56..1..2. aabbccdde ..72..68. afghhiide ..2.87.15 jfggklmme ......3.9 jjgnklopp .7....2.. qqgnooorr 9.634.8.. stuuvwwxx 2.9..8... stuuvvwyz ..41.2... sAuuByyyz .8.4...3. CADDBEEFF a=12 b=17 c=4 d=14 e=15 f=13 g=19 h=7 i=10 j=16 k=10 l=13 m=10 n=15 o=15 p=13 q=11 r=11 s=18 t=3 u=28 v=15 w=20 x=8 y=22 z=12 A=11 B=13 C=6 D=9 E=10 F=5
2.2. Résolution
Le code est globalement le même que le précédent à l’exception de la fonction solver qui vérifie aussi que si la cage est pleine, sa somme est bien égale à celle prévu.
int solver(int *grid, char *cages, int *cages_sum, int i) { int poss_number; int line_id, column_id; int cage_index; if (i == L * L) { return 1; } line_id = i / L; column_id = i % L; if (!grid[i]) { for (poss_number = 1; poss_number < 10 && cages_sum[char_to_index(cages[i]) * 2] >= poss_number; ++poss_number) { if (is_possible(line_id, column_id, grid, poss_number)) { grid[i] = poss_number; cage_index = char_to_index(cages[i]) * 2; if ((cages_sum[cage_index] - poss_number >= cages_sum[cage_index + 1] - 1)) { cages_sum[cage_index] -= poss_number; --cages_sum[cage_index + 1]; if (solver(grid, cages, cages_sum, i + 1)) { return 1; // It's possible to place the number } cages_sum[cage_index] += poss_number; ++cages_sum[cage_index + 1]; } } grid[i] = 0; } return 0; // No possibilities } return solver(grid, cages, cages_sum, i + 1); // Box different to 0 }
2.3. Code complet
#include <math.h> #include <stdio.h> #define L 9 void get_line(int line_id, int *grid, int *line) { int i; for (i = 0; i < L; ++i) { line[i] = grid[line_id * L + i]; } } void get_column(int column_id, int *grid, int *column) { int i; for (i = 0; i < L; ++i) { column[i] = grid[i * L + column_id]; } } void get_square(int line, int column, int *grid, int *square) { int i; int L_root = sqrt(L); for (i = 0; i < L; ++i) { square[i] = grid[(line / L_root * L_root + i / L_root) * L + (column / L_root * L_root + i % L_root)]; } } int is_possible(int i_line, int i_column, int *grid, int number) { int i; int line[L]; int column[L]; int square[L]; get_line(i_line, grid, line); get_column(i_column, grid, column); get_square(i_line, i_column, grid, square); for (i = 0; i < L; ++i) { if (line[i] == number || column[i] == number || square[i] == number) { return 0; } } return 1; } void append_grid(char *line, int *grid, int line_id){ int i; for (i = 0; i < L; ++i) { grid[line_id * L + i] = line[i] == '.' ? 0 : line[i] - 48; } } int char_to_index(char letter){ return letter - 97 < 0 ? letter - 39 : letter - 97; } void cages_index(char *cages, int *index){ int i = 0; int is_letter = 1; int letter_index; while (cages[i] != '\000') { if (is_letter) { letter_index = char_to_index(cages[i]); is_letter = 0; ++i; } else if (cages[i] != ' ') { index[letter_index*2] *= 10; index[letter_index*2] += cages[i] - 48; } else { is_letter = 1; } ++i; } } int solver(int *grid, char *cages, int *cages_sum, int i) { int poss_number; int line_id, column_id; int cage_index; if (i == L * L) { return 1; } line_id = i / L; column_id = i % L; if (!grid[i]) { for (poss_number = 1; poss_number < 10 && cages_sum[char_to_index(cages[i]) * 2] >= poss_number; ++poss_number) { if (is_possible(line_id, column_id, grid, poss_number)) { grid[i] = poss_number; cage_index = char_to_index(cages[i]) * 2; if ((cages_sum[cage_index] - poss_number >= cages_sum[cage_index + 1] - 1)) { cages_sum[cage_index] -= poss_number; --cages_sum[cage_index + 1]; if (solver(grid, cages, cages_sum, i + 1)) { return 1; // It's possible to place the number } cages_sum[cage_index] += poss_number; ++cages_sum[cage_index + 1]; } } grid[i] = 0; } return 0; // No possibilities } return solver(grid, cages, cages_sum, i + 1); // Box different to 0 } int main() { int grid[9][9]; char boxes[9][9]; int cages_values[52][2] = {{0, 0}}; int i, j; for (int i = 0; i < 9; i++) { char grid_line[10]; scanf("%s%s", grid_line, boxes[i]); fgetc(stdin); for (j = 0; j < 9; ++j) { ++cages_values[char_to_index(boxes[i][j])][1]; } append_grid(grid_line, *grid, i); } char cages[251]; scanf("%[^\n]", cages); cages_index(cages, *cages_values); solver(*grid, *boxes, *cages_values, 0); for (i = 0; i < 9; ++i) { for (j = 0; j < 9; ++j) { printf("%d", grid[i][j]); } printf("\n"); } }
2.4. Tests
2.4.1. Test simple
- Input
56..1..2. aabbccdde ..72..68. afghhiide ..2.87.15 jfggklmme ......3.9 jjgnklopp .7....2.. qqgnooorr 9.634.8.. stuuvwwxx 2.9..8... stuuvvwyz ..41.2... sAuuByyyz .8.4...3. CADDBEEFF a=12 b=17 c=4 d=14 e=15 f=13 g=19 h=7 i=10 j=16 k=10 l=13 m=10 n=15 o=15 p=13 q=11 r=11 s=18 t=3 u=28 v=15 w=20 x=8 y=22 z=12 A=11 B=13 C=6 D=9 E=10 F=5
- Output
568913427 197254683 342687915 851726349 473891256 926345871 219538764 734162598 685479132
2.4.2. Test plus compliqué
- Input
......... abbcccddd ......... aabefghii ......... jkkefghil ......... jmnnnooil ......... mmmppqqrl ......... sttpuuqrr ......... svwwwxxxy ......... zvvABBCCy ......... zDDAAEEFF a=7 b=23 c=13 d=13 e=5 f=10 g=17 h=11 i=28 j=12 k=8 l=16 m=20 n=9 o=11 p=22 q=14 r=8 s=15 t=13 u=4 v=17 w=11 x=16 y=8 z=4 A=19 B=10 C=7 D=13 E=15 F=6
- Output
496175238 218369547 753248691 531627489 827594316 649813752 962451873 374982165 185736924