Stuctures de données
Table of Contents
1. Définition
En informatique, une structure de données est une manière d’organiser les données pour les traiter plus facilement. Une structure de données est une mise en oeuvre concrète d’un type abstrait.1
2. Liste Chainée
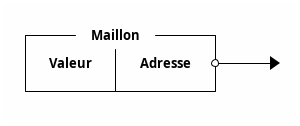
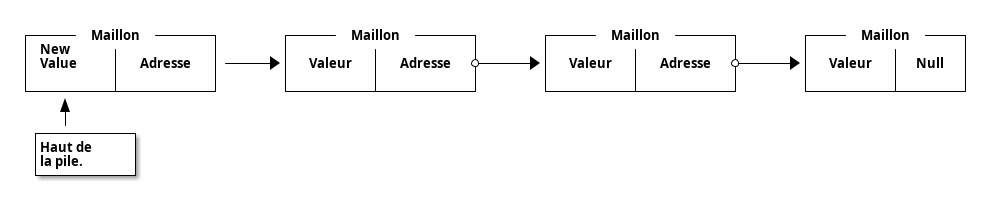
Une Liste Chainée est une colection de données qui permet de stocker une nombre de valeur qui n’est pas nécessairement connu. Chaque élément de cette Liste est appelé Maillon et chaque Maillon d’une liste est de même type. Chaque Maillon est composé :
- D’une valeur
- De l’adresse vers le prochain Maillon de la chaine.
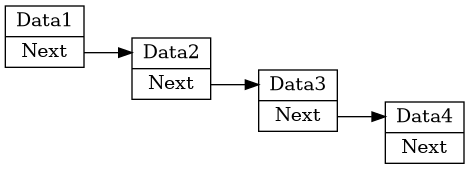
Une Liste Chainée est donc simple une suite de Maillon pointant chacun vers le prochain élément de la liste. Une Liste Chainée est donc en temps que tel seulement un pointeur vers le premier élément de celle-ci.

3. Pile Chainée
Une pile chainée est une structure de donnée respectant le principe du LIFO (pour Last In First Out).
En effet, on peut assimiler cette structure à une pile d’assiette par exemple. Lorsqu’on prend une assiette sur une pile, on prend la dernière assiette qui a été rangée.
Une pile chainée comporte 4 opérations dites primaires.
Il doit être possible de :
- Créer une pile vide.
- Empiler un élément. (Ajouter un élément à la fin de la pile)
- Dépiler un élément. (Enlever le dernier élément de la pile)
- Tester si la pile est vide.
3.1. Implémentation
Pour ce qui est de l’implémentation, j’ai parlé de pile chainée dans le titre de la section. Cela fait donc référence aux maillons encore une fois. Notre pile est donc composée à l’instar de la liste de maillon mis bout à bout.
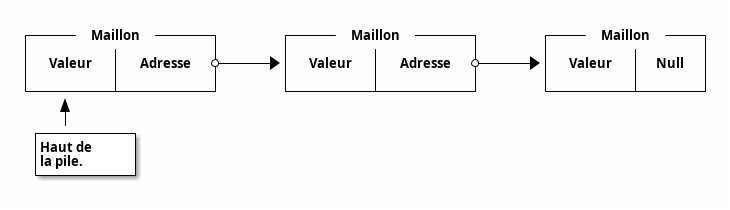
3.1.1. Empiler
Lorsqu’on empile, on vient rajouter un élément au début de la pile.
3.1.2. Dépiler
Le dépilage est donc l’opération inverse puisque que l’on vient enlever le dernier élément ajouté.
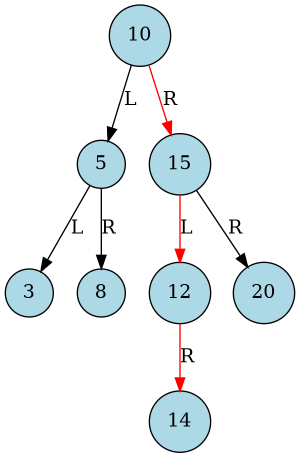
4. Arbre Binaire de Recherche
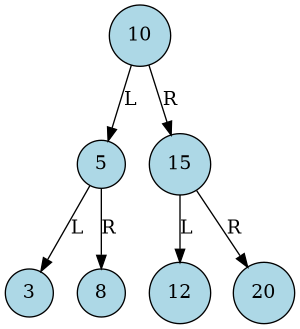
Un arbre binaire de recherche est un arbre binaire dans lequel chaque nœud possède une clé, telle que chaque nœud du sous-arbre gauche ait une clé inférieure ou égale à celle du nœud considéré, et que chaque nœud du sous-arbre droit possède une clé supérieure ou égale à celle-ci — selon la mise en œuvre de l’ABR, on pourra interdire ou non des clés de valeur égale. Les nœuds que l’on ajoute deviennent des feuilles de l’arbre.
4.1. Insertion
L’insertion dans l’ABR est un peu compliquée. Comme on l’a dit plus tôt l’avantage incontestable de l’ABR est que les valeurs de l’arbres sont ordonées. Les recherches sont donc très rapide (\(0(\log_2(n))\)).
Cependant, cela implique que l’insertion de l’élement doit se faire aussi de manière ordonée. Lorsqu’on ajoute un élément, cela ce fait récursivement. On commence par la racine de l’arbre:
- Si la racine est vide, on place l’élement.
- Sinon,
- Si l’élément est supérieur à la racine, on recommence en essayant de le placer dans le fils droit de la racine.
- Sinon on le place à gauche de la racine.
4.1.1. Exemple
On insère 14 dans l’arbre précédent.