Min Max
Table of Contents
1. Min Max
2. Présentation
Il nous est donné un zero-sum game à 2 joueurs. Chaque joueur joue l’un après l’autre.
Le jeu dure D tours et à chaque tour, le joeur a le choix entre B coups possibles.
On considère le jeu comme assez cour pour modéliser entièrement l’arbre des décisions de la partie et pouvoir trouver le meilleur coup possible grâce à l’algorithme minmax : https://en.wikipedia.org/wiki/Minimax.
Afin d’améliorer la complexité de notre algorithme, il est possible d’utiliser la technique d’élaguage Alpha : https://en.wikipedia.org/wiki/Alpha-beta_pruning
L’objectif est donc de fournir le meilleur choix que l’ordinateur devrait choisir pour gagner.
2.1. Input
D B Leafs
Avec :
- D la profondeur de l’arbre de décision
- B le nombre de branches par noeuds
- Leafs l’ensemble des feuilles de l’arbre de décisions.
2.2. Output
Le meilleur coup a choisir.
3. Résolution
Je précise que ma solution ne fonctionne pas à 100 %. Pour plus de détails sur l’aspect technique des fonctions et des structures : documentation.
3.1. Programme principale
/** * Auto-generated code below aims at helping you parse * the standard input according to the problem statement. **/ int main() { int D; int B; int i; int temp; node_t *test = malloc(sizeof(node_t)); int alpha = -1000, beta = 1000; scanf("%d %d", &D, &B); int nb_leafs = pow(B, D); int_list *leafs = malloc(sizeof(int_list)); for (i = 0; i < nb_leafs; ++i) { scanf("%d", &temp); il_append(leafs, temp); } il_show(leafs); node_t *tree = create_tree(0, D, B, leafs); tree_show(tree); // Write an answer using printf(). DON'T FORGET THE TRAILING \n // To debug: fprintf(stderr, "Debug messages...\n"); // int result = alphabeta(tree, D, alpha, beta, D % 2); // printf("%d 0\n", result); return 0; }
Après avoir récupéré B et D. On stocke ensuite toutes les feuilles dans une liste et on créer l’arbre de décision qui lui correspond. On appelle enfin la fonction alphabeta qui nous donne le resultat.
3.1.1. Exemple
Pour l’input suivant :
1 4 2 -1
On obtient l’arbre suivant :
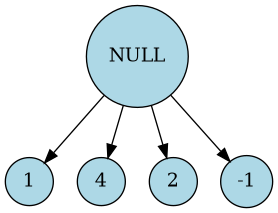
3.2. Fonction alpha beta
int alphabeta(node_t *node, int depth, int alpha, int beta, int is_max) { int value; int result; if (depth == 0) { return node->value; } if (is_max) { value = -1000; for (int i = 0; i< 4; ++i) { node_t *child = node->children[i]; result = alphabeta(child, depth - 1, alpha, beta, 0); if (value < result) { value = result; } if (value > alpha) { alpha = value; } if (value >= beta) { break; } } return value; } else { value = 1000; for (int i=0 ; i<4; ++i) { node_t *child = node->children[i]; result = alphabeta(child, depth - 1, alpha, beta, 1); if (value < result) { value = result; } if (value < beta) { beta = value; } if (value <= alpha) { break; } } return value; } }
Cette fonction applique le principe d’élaguage alpha beta sur notre arbre. Le principe de cet élagage est de réduire le nombre de noeuds visités.
Pour cela on va à chaque fois la plus grande et la plus petite valeur possible pour ce noeud. Puisqu’un exemple vaut mieux que mille mots, en voici un :
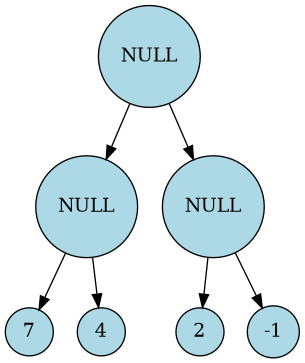 Nous avons ici la position de base. En comment l’algo, nous allons donc choisir le minimum pour les feuilles. Commençons :
Nous avons ici la position de base. En comment l’algo, nous allons donc choisir le minimum pour les feuilles. Commençons :
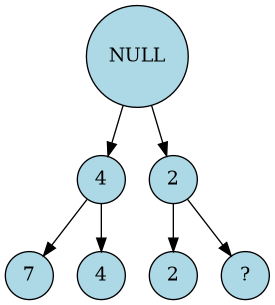 Il faut maintenant choisir un maximum pour le deuxième étage. Seulement nous avons un 2 dans le deuxième fils. Peu importe la valeur du dernier noeud, puisque l’on garde la plus petite des feuilles, on aura rien au dessus de 2 et donc rien au dessu de quatre. La dernière feuille est donc élaguée.
Il faut maintenant choisir un maximum pour le deuxième étage. Seulement nous avons un 2 dans le deuxième fils. Peu importe la valeur du dernier noeud, puisque l’on garde la plus petite des feuilles, on aura rien au dessus de 2 et donc rien au dessu de quatre. La dernière feuille est donc élaguée.
On continue ici jusqu’à arriver à la racine. On obtient alors le meilleur voup a jouer pour l’ordinateur.
4. Code complet
cat ../sources/minmax.c
/* [[file:../org/minmax.org::*Includes][Includes:1]] */ #include <math.h> #include <stdbool.h> #include <stdio.h> #include <stdlib.h> /* Includes:1 ends here */ /** * \file minmax.c * \author Arthur Barraux * \brief Documentation pour le programme résolvant le problème Minimax Exercise * de codingame \version 1.0 \date 23 avril 2024 */ /* [[file:../org/minmax.org::*Structures][Structures:1]] */ /** * \struct Maillon_int * \brief Structure maillon pour une liste d'entier */ typedef struct Maillon_int { int value; /**< Valeur du Maillon*/ struct Maillon_int *next; /**< Pointeur vers le prochian Maillon*/ } Maillon_int; typedef struct { Maillon_int *head; } int_list; /** *\struct node_t *\brief Structure noeud d'un arbre*/ typedef struct node { int value; /**< Valeur du noeud*/ struct node **children; /**< Pointeur vers le premier Maillon de la liste des enfants de ce noeud*/ } node_t; /* Structures:1 ends here */ /* [[file:../org/minmax.org::*Fonctions][Fonctions:1]] */ /** * \fn bool nl_is_empty(Maillon_node *maillon) * \brief Teste si une Maillon est vide * \param maillon Un élément de type Maillon * \return 1 si le Maillon est NULL sinon 0 */ bool have_children(node_t *tree) { return tree->children != NULL; } void il_append(int_list *liste, int value) { Maillon_int *new = malloc(sizeof(Maillon_int)); new->value = value; new->next = liste->head; liste->head = new; } /** * \fn Maillon_int *il_pop(Maillon_int *maillon) * \brief Enlève le premier élément de la liste */ void il_pop(int_list *liste) { Maillon_int *new_head = liste->head->next; free(liste->head); liste->head = new_head; } /** * \fn node_t *create_tree(int depth, int max_depth, int branching_factor) * \brief Créer un arbre de prondeur max_depth et de nombre de branche par noeud * égal à branching_factor * \param depth profondeur de laquelle on commence l'arbre * \param max_depth Profondeur max de l'arbre * \param branching_factor Nombre de branches par noeuds * \return Renvoie la racine de l'arbre */ node_t *create_tree(int depth, int max_depth, int branching_factor, int_list *leafs, node_t *tree) { if (depth == max_depth) { tree->value = leafs->head->value; il_pop(leafs); return tree; } for (int i = 0; i < pow(branching_factor, depth); ++i) { // printf("%d\n", i); for (int j = 0; j < branching_factor; ++j) { node_t *node = create_tree(depth + 1, max_depth, branching_factor, leafs, tree); tree->children[j] = node; } } } void search_min(int branching_factor, int *leafs, int nb_leafs, int *beta) { int i; for (i = 0; i < nb_leafs; ++i) { if (leafs[i - i % branching_factor] > leafs[i]) { *beta = leafs[i]; } } } void search_max(int branching_factor, int *leafs, int nb_leafs, int *alpha) { int i; for (i = 0; i < nb_leafs; ++i) { if (leafs[i - i % branching_factor] < leafs[i]) { *alpha = leafs[i]; } } } int alphabeta(node_t *node, int depth, int alpha, int beta, int is_max) { int value; int result; if (depth == 0) { return node->value; } if (is_max) { value = -1000; for (int i = 0; i < 4; ++i) { node_t *child = node->children[i]; result = alphabeta(child, depth - 1, alpha, beta, 0); if (value < result) { value = result; } if (value > alpha) { alpha = value; } if (value >= beta) { break; } } return value; } else { value = 1000; for (int i = 0; i < 4; ++i) { node_t *child = node->children[i]; result = alphabeta(child, depth - 1, alpha, beta, 1); if (value < result) { value = result; } if (value < beta) { beta = value; } if (value <= alpha) { break; } } return value; } } void il_show(int_list *liste) { for (Maillon_int *m = liste->head; m != NULL; m = m->next) { printf("%d -> ", m->value); } printf("\n"); } void tree_show(node_t *tree) { if (!have_children(tree)) { printf("%d ", tree->value); } for (int i = 0; i < 4; ++i) { tree_show(tree->children[i]); } } /* Fonctions:1 ends here */ /* [[file:../org/minmax.org::*Main][Main:1]] */ /** * Auto-generated code below aims at helping you parse * the standard input according to the problem statement. **/ int main() { int D; int B; int i; int temp; node_t *test = malloc(sizeof(node_t)); int alpha = -1000, beta = 1000; scanf("%d %d", &D, &B); int nb_leafs = pow(B, D); int_list *leafs = malloc(sizeof(int_list)); for (i = 0; i < nb_leafs; ++i) { scanf("%d", &temp); il_append(leafs, temp); } il_show(leafs); node_t *tree = malloc(sizeof(node_t)); create_tree(0, D, B, leafs, tree); // tree_show(tree); // Write an answer using printf(). DON'T FORGET THE TRAILING \n // To debug: fprintf(stderr, "Debug messages...\n"); int result = alphabeta(tree, D, alpha, beta, D % 2); // printf("%d 0\n", result); return 0; } /* Main:1 ends here */
5. Tests
Malheureusement, mon code ne fonctionnant toujours pas, je ne pourrai pas vous montrer le résultat des tests. Je travailles toujours sur ma solution en espérant pouvoir vous la présenter un jour …