Dwarf Standing On Shoulders of Giants
Table of Contents
1. Présentation
Lorsqu’on lit des textes, on se dit souvent : “Cette personne doit influencer celle-là”. Plus tard, on se rend finalement compte que la deuxième personne influence elle-même une troisième personne. Dans cet exercice, on s’intéresse à ces chaines d’influence et plus précisement au fait de trouver la plus longue.
1.1. Input
N X Y
N est le nombre de relations d’influences Pour chaque relation d’influence, il nous et donné X Y indiquant que X influence Y.
1.2. Output
La longueur de la plus grande chaîne d’influence.
1.3. Exemple
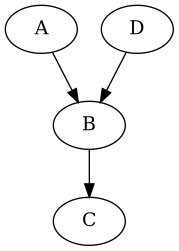 Voici un schéma où:
Voici un schéma où:
- A influence B
- B influence C
- D influence B
2. Résolution
int main(){ int n; int i; int dwarf; int giant; scanf("%d", &n); // Number of connections int connection[100][100] = {{0}}; int longuest_path = 0; int path_length = 0; for (i=0; i<n; ++i) { scanf("%d", &dwarf); // Connection input "1 3" scanf("%d", &giant); connection[dwarf - 1][giant - 1] = 1; } for (i=0; i<n; ++i){ path_length = longuest_path(connection, n, i); longuest_path = path_length > longuest_path ? path_length : longuest_path; } printf("%d\n", longuest_path + 1); return 0; }
On créer une constante donnant la valeur maximum des indices. (MAX\INDEX) On récupère le nombre de relation. On considérera les relations d’influence comme un graphe orienté. On créer ainsi la matrice d’adjacence de taille \(MAX\_INDEX * MAX\_INDEX\) On récupère maintenant tout les couples de relation et l’on met un 1 à la case d’indice X, Y afin d’indiquer la connection. Enfin on applique la fonction longuest\path à a chaque élément de du graph. Pour finir on renvoie la longueur maximum + 1 de l’opération précédente.
2.1. Détails de la fonction longuest\path
int max(int *children, int length){ int i; int max = children[0]; for (i=1; i<length; ++i){ if(children[i] > max){ max = children[i]; } } return max; } int longuest_path(int graph[][100], int graph_len, int start){ int i; int nb_children; int children[graph_len]; for(i=0; i<graph_len; ++i){ if (graph[start][i] != 0){ children[i] = longuest_path(graph, graph_len, i); } else { children[i] = 0; } } return max(children, graph_len) + 1; }
La fonction longuest\path prend en argument la matrice d’adjacence, sa taille et l’indice de l’élément dont on veut connaitre le nombre de connections. On créer un tableau pour stocker le nombre de connection de ses connections de premier degré. (children) Pour chaque connection trouvé avec cet élément :
- On ajoute à children longuest\path en partant cette fois du nouvelle élément et ainsi de suite.
- On fini par renvoyer le maximum de /
2.2. Détails de la fonction max
La fonction Max prend en argument un tableau d’entier et renvoie bêtement le maximum de ce tableau. Je ne pense pas que cette fonction mérite plus ample explications.
3. Tests détaillés
3.1. Test simple
3.1.1. Input
cat ../tests/test_dosog.txt
Voici le schéma associé à cet exemple:
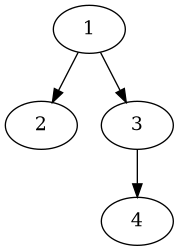
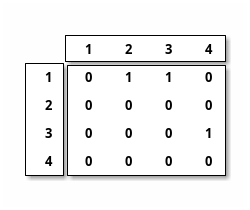
3.1.2. Matrice d’adjacence
Voici la matrice d’adjacence associée (en considérence le nom des noeuds).
3.1.3. Output
./../bin/dosog < ../tests/test_dosog.txt
3.2. Test un peu plus compliqué
3.2.1. Input
cat ../tests/test_dosog_2.txt
Voici le schéma associé à cet exemple:
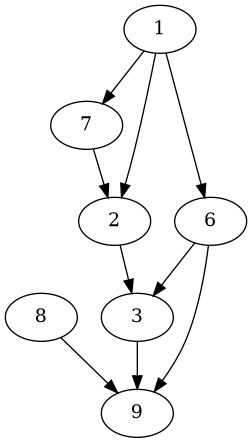
3.2.2. Matrice d’adjacence
Voici la matrice d’adjacence associée (en considérence le nom des noeuds).
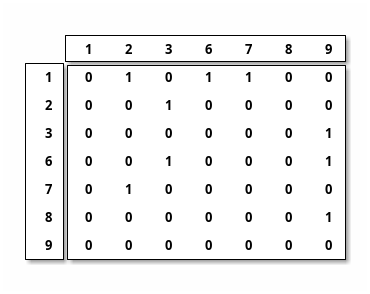
3.2.3. Output
./../bin/dosog < ../tests/test_dosog_2.txt
4. Conclusion
J’ai beaucoup apprécié cet exercice car il traitait des graphes et de parcours de ceux-cis. J’ai cependant rencontré quelques difficultés pour le résoudre ce qui le rend encore plus intéressant.